sdut 2153 Clockwise (2010年山东省第一届ACM大学生程序设计竞赛)

题目大意:

n个点，第i个点和第i+1个点可以构成向量，问最少删除多少个点可以让构成的向量顺时针旋转或者逆时针旋转。

分析：

dp很好想，dp[j][i]表示以向量ji（第j个点到第i个点构成的向量）为终点的最大顺时针/逆时针向量数。状态转移方程为 dp[j][i] = max{dp[k][j]+1}。

问题个关键是如何判断2个向量是顺时针还是逆时针。

计算几何用的知识是求叉积和点积，叉积的作用是判断两个向量的左右（顺逆），点积的作用是判断两个向量的前后。举个例子，假设有2个向量v1，v2，‘*’暂时代表叉积运算，‘·’暂时代表点积运算。叉积判定：如果v1*v2>0，则v1在v2的顺时针方向；如果v1*v2=0，则v1、v2共线；如果v1*v2<0，则v1在v2的逆时针方向。点积判定：如果v1·v2>0，则v1和v2都指向同一侧面；如果v1·v2=0，则v1和v2垂直；如果v1·v2<0，则v1和v2都指向相反的侧面。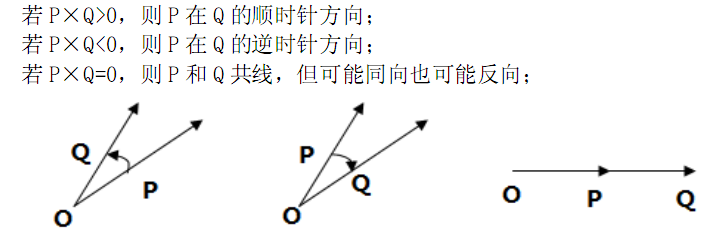

顺时针的旋转范围是(0<=T<180)，逆时针的旋转范围是(0<T<=180)，也就是说如果两条向量共线的话，顺时针旋转可以同方向（T=0），不能反方向；逆时针旋转可以反方向（T=180），不能同方向。

  1 #include<cstdio>
  2 #include<cstring>
  3 #include<iostream>
  4 #include<cmath>
  5 #include<algorithm>
  6 #include<set>
  7 #include<queue>
  8 #include<stack>
  9 #define MAXN 310
 10 
 11 using namespace std;
 12 int dp[MAXN][MAXN],n;
 13 struct Point
 14 {
 15     int x,y;
 16     Point (int x_=0,int y_=0):x(x_),y(y_) {}
 17 } p[MAXN];
 18 typedef Point Vector;
 19 Vector operator -(Point a,Point b)
 20 {
 21     return Vector(a.x-b.x,a.y-b.y);
 22 }
 23 int  Cross(Vector a,Vector b)//向量叉积
 24 {
 25     return a.x*b.y-a.y*b.x;
 26 }
 27 int Dot(Vector a,Vector b)//向量点乘
 28 {
 29     return a.x*b.x+a.y*b.y;
 30 }
 31 int if_shun(int i,int j,int k)//判断顺时针
 32 {
 33     
 34     Vector v1=p[i]-p[j];
 35     Vector v2=p[j]-p[k];
 36     int tem=Cross(v1,v2);
 37     if(tem>0)
 38         return 1;
 39     else if(tem<0)
 40         return 0;
 41     if(tem==0)
 42     {
 43         int tem1=Dot(v1,v2);
 44         if(tem1<0)
 45             return 0;
 46         return 1;
 47     }
 48 }
 49 int if_ni(int i,int j,int k)//判断逆时针
 50 {
 51    
 52     Vector v1=p[i]-p[j];
 53     Vector v2=p[j]-p[k];
 54     int tem=Cross(v1,v2);
 55     if(tem>0)
 56         return 0;
 57     else if(tem<0)
 58         return 1;
 59     if(tem==0)
 60     {
 61         int tem1=Dot(v1,v2);//向量共线，判断一下方向
 62         if(tem1<0)
 63             return 1;
 64         return 0;
 65     }
 66 }
 67 int puan_shun()
 68 {
 69     int ans=0;
 70     //dp[0][1]=1;
 71     for(int i=0; i<n; i++)
 72     {
 73         for(int j=0; j<i; j++)
 74         {
 75             dp[j][i]=1;
 76             for(int k=0; k<j; k++)
 77             {
 78                 if(if_shun(i,j,k))
 79                     dp[j][i]=max(dp[j][i],dp[k][j]+1);
 80             }
 81             ans=max(ans,dp[j][i]);
 82         }
 83 
 84     }
 85     return ans;
 86 }
 87 int puan_ni()
 88 {
 89     int ans=0;
 90     //dp[0][1]=1;
 91     for(int i=0; i<n; i++)
 92     {
 93         for(int j=0; j<i; j++)
 94         {
 95             dp[j][i]=1;
 96             for(int k=0; k<j; k++)
 97             {
 98                 if(if_ni(i,j,k))
 99                     dp[j][i]=max(dp[j][i],dp[k][j]+1);
100             }
101             ans=max(ans,dp[j][i]);
102         }
103 
104     }
105     return ans;
106 }
107 
108 int main()
109 {
110     while(scanf("%d",&n)!=EOF&&n)
111     {
112         for(int i=0; i<n; i++)
113             scanf("%d %d",&p[i].x,&p[i].y);
114         memset(dp,0,sizeof(dp));
115         int ans1=puan_shun();
116         memset(dp,0,sizeof(dp));
117         int ans2=puan_ni();
118         //printf("%d %d==\n",ans1,ans2);
119         if(ans1==n-1)
120             printf("C\n");
121         else if(ans2==n-1)
122             printf("CC\n");
123         else if(ans1>=ans2)
124             printf("Remove %d bead(s), C\n",n-ans1-1);
125         else
126             printf("Remove %d bead(s), CC\n",n-ans2-1);
127         printf("\n");
128     }
129     return 0;
130 }

 

posted on 2015-04-21 23:49  tsw123  阅读(290)  评论(0)  编辑  收藏  举报

导航