CS231n Lecture5-Convolutional Neural Networks学习笔记
一、Architecture Overview
- Regular Neural Nets and Convolutional Neural Networks(插图)

1. Layers used to build ConvNets
- 一般由卷积层、池化层、全连接层组成。
- 但是卷积层和池化层之间,一般也有激活函数层
- 每一层的接收参数是一个三维的输入,同时通过不同的函数输出一个三维的数据
- 卷积层和全连接层有参数;而激活函数层和池化层没有参数。
- 卷积层、全连接层和池化层可能有额外的超参数,但是激活函数层没有。
- 讲解插图

二、Convolutional Layer
-
Local Connectivity: 我们使用卷积核(或者叫感受野receptive field)进行连接,这个部分就是和之前普通的神经网络的区别,这一部分的参数是共享的,可以节省很多的资源。
-
Spatial arrangement: 三个重要的超参数,一个是深度(depth)、步长(stride)、0填充(zero-padding)。深度即输出结果中的通道的数量,有多少个卷积核就是深度多少;步长就是卷积和在图像上滑动的尺寸大小;0填充就是在输入数据的周围填充上全为0的数据。
-
计算输出尺寸: 输入尺寸的大小为
W;卷积核的尺寸大小为F;步长为S;0填充的大小为P;输出尺寸大小为(W-F+2*P)/S+1(插图)

-
使用0填充原因: 就是保持输入尺寸大小和输出尺寸的大小相同;同时有时候步长的设置,如果不使用填充,会出现输出结果是小数的情况,这时是无效的,因此需要填充。
-
Parameter Sharing: 就是讲的卷积核的参数是共享的。
-
卷积核与局部区域是怎样操作的: 我们知道的是卷积核一般的形式是
5x5x3,3代表的是原来输入数据的深度即通道数,我们在实际操作就是把把卷积核拉伸成一个一维向量,同时与卷积核重合部分,也拉伸成一个5x5x3=75的一维向量,那么这两部分便可以进行点积运算了。最后得到一个数字,便是该卷积核下新生成的一个像素点。例如原来送入尺寸为227x227x3,卷积核大小为11x11x3=363,步长为4,不使用填充,根据公式计算得(227-11)/4+1=55,使用卷积核的数量为96个,意味着输出尺寸的通道数为96,输出尺寸变为55x55x96,结合前面的讲解看成卷积核部分拉伸为一维向量,那么可以看成卷积核96x363和输入363x3025的矩阵乘法运算,也就是点积最后结果为96x3025=55x55x96 -
Backpropagation: 卷积运算(对于数据和权重)的后向传递也是卷积(但是使用了空间翻转的过滤器)
-
1x1 convolution:
-
Dilated convolutions:
-
案例:
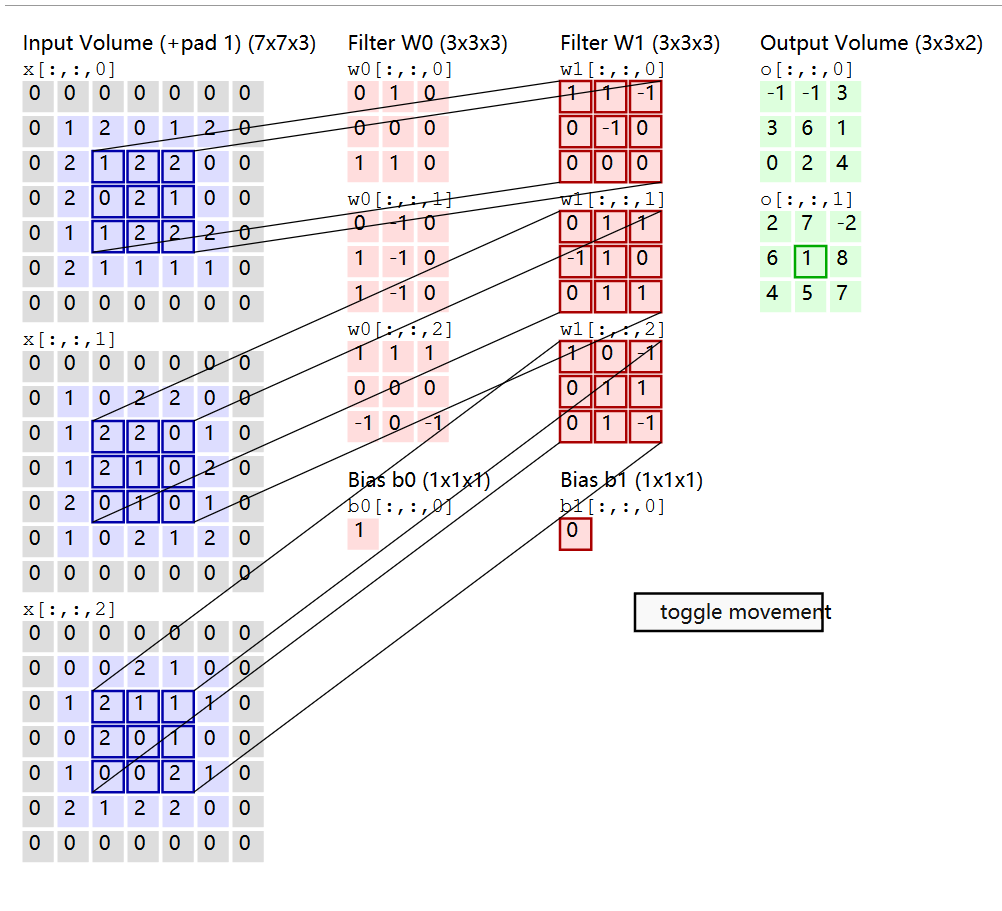
三、Pooling Layer, Normalization Layer and Fully-connected layer
- 简单来讲就是下采样,减少尺寸,控制过拟合,深度是保留的不改变,即通道数。
-
尺寸计算: 插图

-
General pooling: 一般有最大池化、平均池化、L2范式池化。
-
Backpropagation:
-
一些网络结构中可能也会丢弃池化层
-
归一化层,已经失效在一些网络结构中,同时一些实验也证明,这个部分对于结果的贡献是很小的。
-
全连接层,就是最后一层数据拉成一维向量,进行后续运算,产生每个类型的分数。
四、Converting FC layers to CONV layers
- 没懂
五、ConvNet Architectures
INPUT -> [[CONV -> RELU]*N -> POOL?]*M -> [FC -> RELU]*K -> FC- 一般卷积网络结构,如上所示,N是模块重复的次数一般大于
0小于3,其他数量参数同理。 - 更喜欢用几个小的卷积核层而不是一个大的卷积核层来达成相同大小的尺寸。原因如下:1. 多层的卷积层包含非线性,使得它们的特征更具表现力;2. 可以使用更少的参数表达更强大的输入特性。缺点:可能需要更多的内存来容纳所有中间卷积层的结果,如果我们进行反向传播。
- 一些常见参数,输入尺寸一般是
32, 64, 96, 224, 384, 512,卷积层中的卷积核F与步长S和填充P的关系,假设步长S=1,如果想保持原来尺寸大小,那么P = (F - 1)/2 - Why use stride of 1 in CONV? 允许我们留取更多的空间给池化层,同时同时仅仅转化了通道的数量。
- Why use padding? 除了之前提到的保持空间大小不变,还可以提高性能,更有效的提取特征信息,因为过快的缩小尺寸会丢失很多有效信息。
六、Case Studies
-
LeNet: 上世纪90年代成功的应用卷积网络,被用于邮政编码的识别。Paper
-
AlexNet: 第一个在计算机视觉上受欢迎的工作,在2012的 ImageNet ILSVRC challenge比赛中成绩远高于第二名。结构上和LeNet相识,但是网络更深,更大。Paper
-
ZF Net: 它是对AlexNet的一个改进,通过调整架构超参数,特别是通过扩展中间卷积层的大小,并使第一层的stride和filter的大小更小。Paper
-
GoogLeNet: 2014年ILSVRC的获奖者是来自谷歌的Szegedy等人的卷积网络。它的主要贡献是先启模块的开发,该模块极大地减少了网络中的参数数量(4M,而AlexNet只有60M)。此外,本文在ConvNet的顶部使用平均池而不是完全连接的层,从而消除了大量似乎不太重要的参数。Paper
-
VGGNet: 2014年ILSVRC的亚军是Karen Simonyan和Andrew Zisserman创办的VGGNet。它的主要贡献是表明网络的深度是良好性能的一个关键组成部分。他们最终的最佳网络包含16个CONV/FC层,并且,令人感兴趣的是,具有一个非常同构的架构,从开始到结束只执行3x3的卷积和2x2的池。他们预先训练的模型可以在caffe中即插即用。VGGNet的一个缺点是它的计算开销更大,并且使用了更多的内存和参数(1.4亿)。这些参数中的大多数都位于第一个全连接层中,从那以后,我们发现可以删除这些FC层而不会降低性能,从而显著减少了所需参数的数量。Paper
-
ResNet: 由何开明等人开发的残差网络获得了2015年ILSVRC的冠军。它具有特殊的跳过连接和大量使用批处理规范化。该架构还缺少网络末端的全连接层。读者还可以参考kaim的演示(视频、幻灯片)和一些最近在Torch中复制这些网络的实验。ResNets目前是最先进的卷积神经网络模型,是在实践中使用卷积神经网络的默认选择(截至2016年5月10日)。尤其值得注意的是,最近出现了更多的变化。Paper
-
VGGNet in detail.:
INPUT: [224x224x3] memory: 224*224*3=150K weights: 0
CONV3-64: [224x224x64] memory: 224*224*64=3.2M weights: (3*3*3)*64 = 1,728
CONV3-64: [224x224x64] memory: 224*224*64=3.2M weights: (3*3*64)*64 = 36,864
POOL2: [112x112x64] memory: 112*112*64=800K weights: 0
CONV3-128: [112x112x128] memory: 112*112*128=1.6M weights: (3*3*64)*128 = 73,728
CONV3-128: [112x112x128] memory: 112*112*128=1.6M weights: (3*3*128)*128 = 147,456
POOL2: [56x56x128] memory: 56*56*128=400K weights: 0
CONV3-256: [56x56x256] memory: 56*56*256=800K weights: (3*3*128)*256 = 294,912
CONV3-256: [56x56x256] memory: 56*56*256=800K weights: (3*3*256)*256 = 589,824
CONV3-256: [56x56x256] memory: 56*56*256=800K weights: (3*3*256)*256 = 589,824
POOL2: [28x28x256] memory: 28*28*256=200K weights: 0
CONV3-512: [28x28x512] memory: 28*28*512=400K weights: (3*3*256)*512 = 1,179,648
CONV3-512: [28x28x512] memory: 28*28*512=400K weights: (3*3*512)*512 = 2,359,296
CONV3-512: [28x28x512] memory: 28*28*512=400K weights: (3*3*512)*512 = 2,359,296
POOL2: [14x14x512] memory: 14*14*512=100K weights: 0
CONV3-512: [14x14x512] memory: 14*14*512=100K weights: (3*3*512)*512 = 2,359,296
CONV3-512: [14x14x512] memory: 14*14*512=100K weights: (3*3*512)*512 = 2,359,296
CONV3-512: [14x14x512] memory: 14*14*512=100K weights: (3*3*512)*512 = 2,359,296
POOL2: [7x7x512] memory: 7*7*512=25K weights: 0
FC: [1x1x4096] memory: 4096 weights: 7*7*512*4096 = 102,760,448
FC: [1x1x4096] memory: 4096 weights: 4096*4096 = 16,777,216
FC: [1x1x1000] memory: 1000 weights: 4096*1000 = 4,096,000
TOTAL memory: 24M * 4 bytes ~= 93MB / image (only forward! ~*2 for bwd)
TOTAL params: 138M parameters
七、Computational Considerations
- There are three major sources of memory to keep track of:
- 存储中间数据
- 参数的大小,梯度
- 必须维护各种各样内存,如图像数据批,也许他们的增强版本,等等。



