《计算机组成与设计:硬件/软件接口》第三章 计算机的算术运算笔记
第三章 计算机的算术运算笔记
3.2 加法和减法
加减法的溢出条件
有符号整数
| 操作 | 操作数A | 操作数B | 表示有溢出的条件 |
|---|---|---|---|
| A+B | >= 0 | >= 0 | <0 |
| A+B | < 0 | < 0 | >=0 |
| A-B | >= 0 | < 0 | <0 |
| A-B | < 0 | >= 0 | >=0 |
检测代码
# check $t1 + $t2
xor $t3, $t1, $t2 # check if the signs of two oprands are different.
slt $t3, $t3, $zero # if differs, $t3 will be negative, and thus less than zero and set to 1
bne $t3, $zero, NO_OVERFLOW # if deffers, overflow won't ever happens
addu $t4, $t1, $t2 # $t4 = sum, but don't trap
xor $t3, $t4, $t1 # check if the result's sign match the ideal sign
slt $t3, $t3, $zero # if differs, $t3 will be negative, and thus less than zero and set to 1
bne $t3, $zero, OVERFLOW
无符号整数
可以忽略。
由于无符号数通常用于表示内存地址,这种情况下的溢出可以忽略 --p119
检测代码
not $t3, $t1, $zero
sltu $t3, $t3, $t2
bne $t3, zero, OVERFLOW
3.3 乘法
硬件(填空)
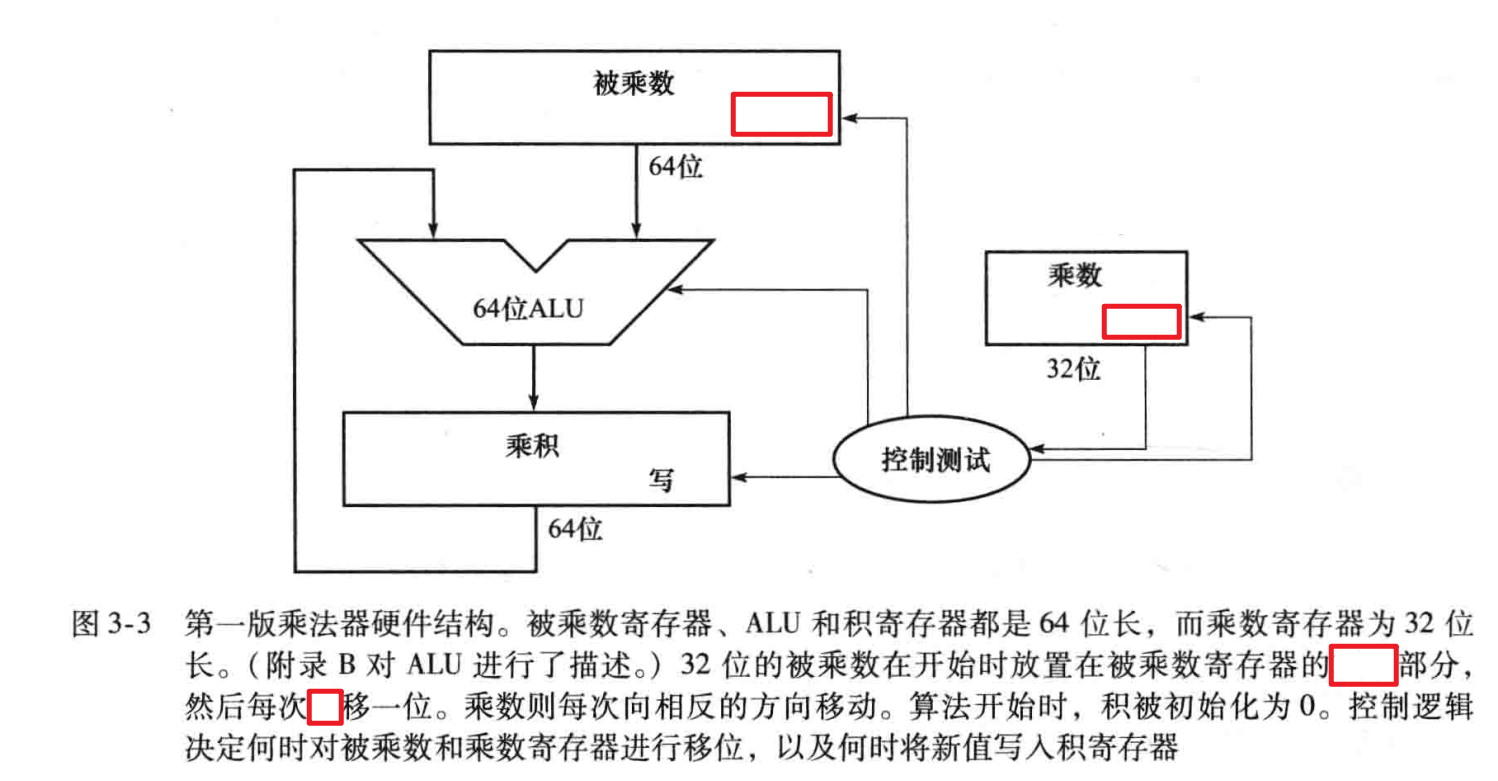
流程
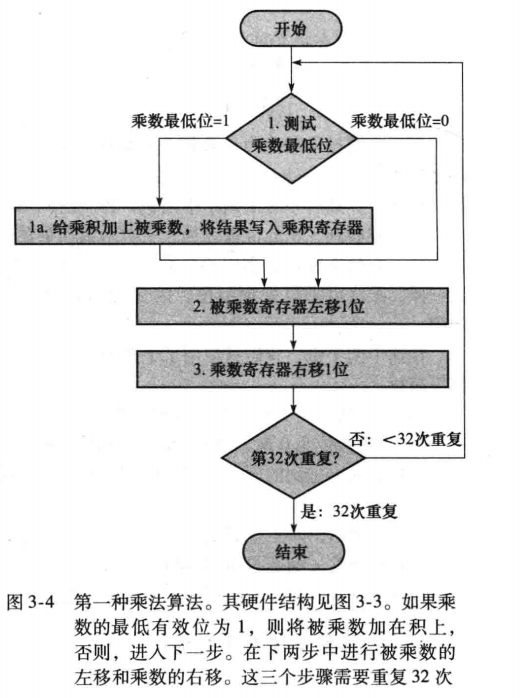
- 测试乘数最低位
- 若为 1,则在乘积加上被乘数
- 若为 0,则继续
- 左移被乘数
- 右移乘数
- 判断是否进行了 32 次
- 是则退出
- 否则返回 1
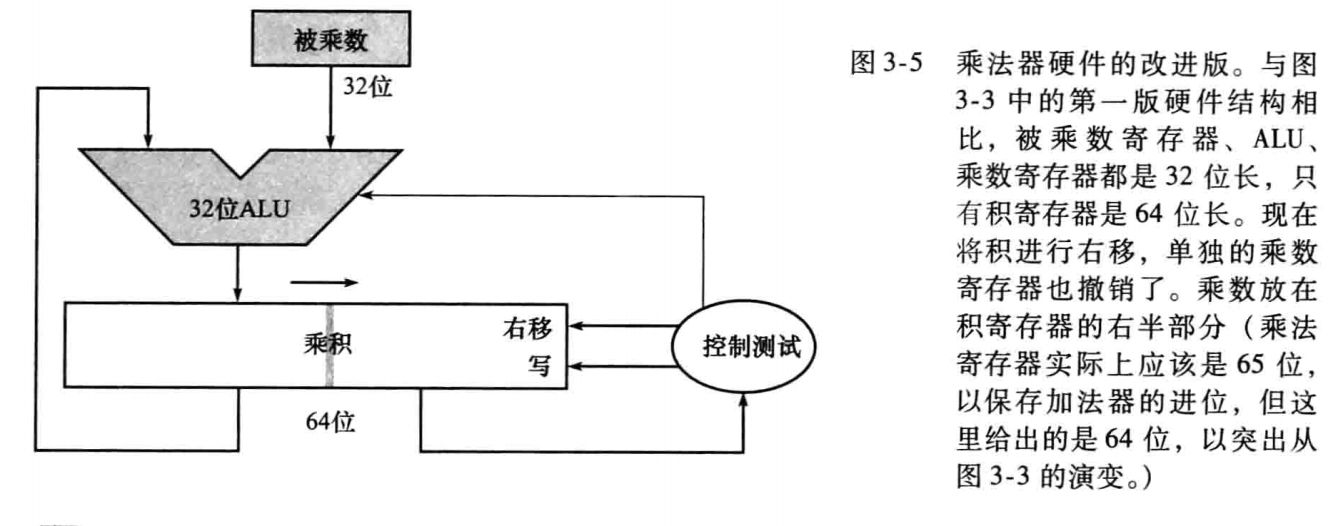
改进
被乘数左移,相对来说就是乘积右移,因此可以把乘积和乘数放在一块一起右移。
因为乘积不会一下到64位,而乘数每次都可以丢弃一位,因此是合理的。
3.4 除法
搞懂乘法,除法就不难了。
硬件(填空)
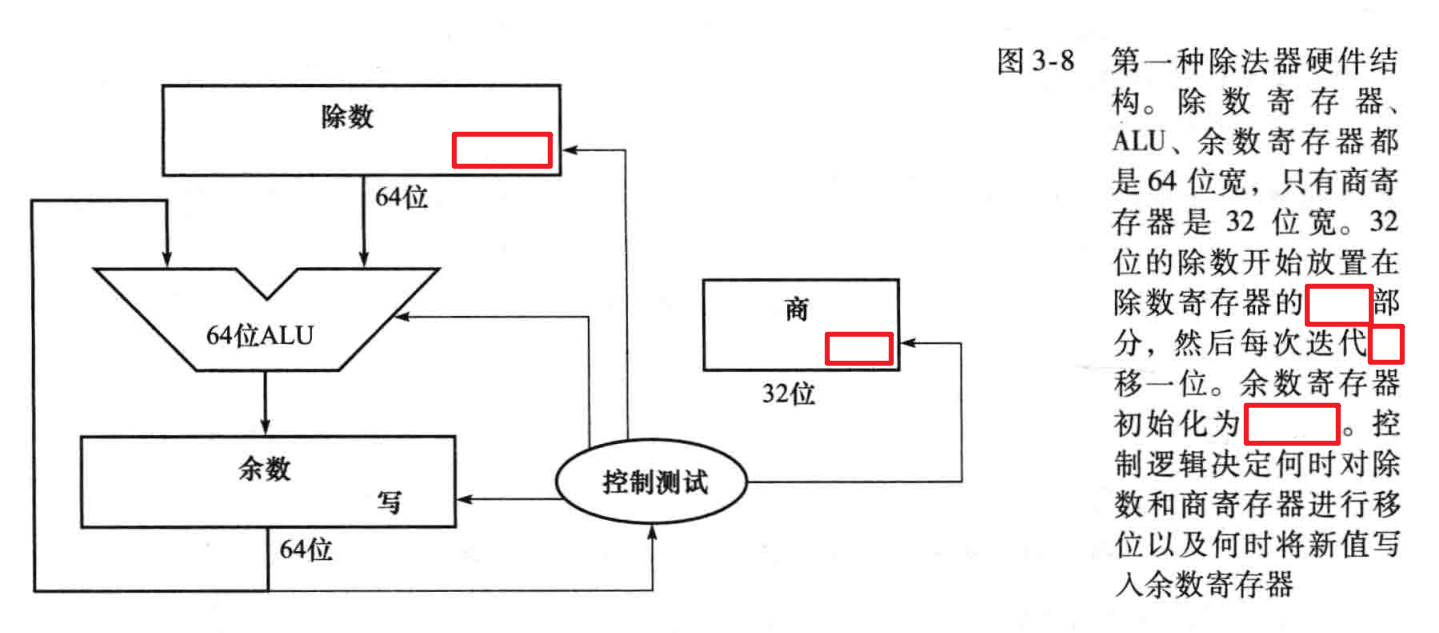
流程
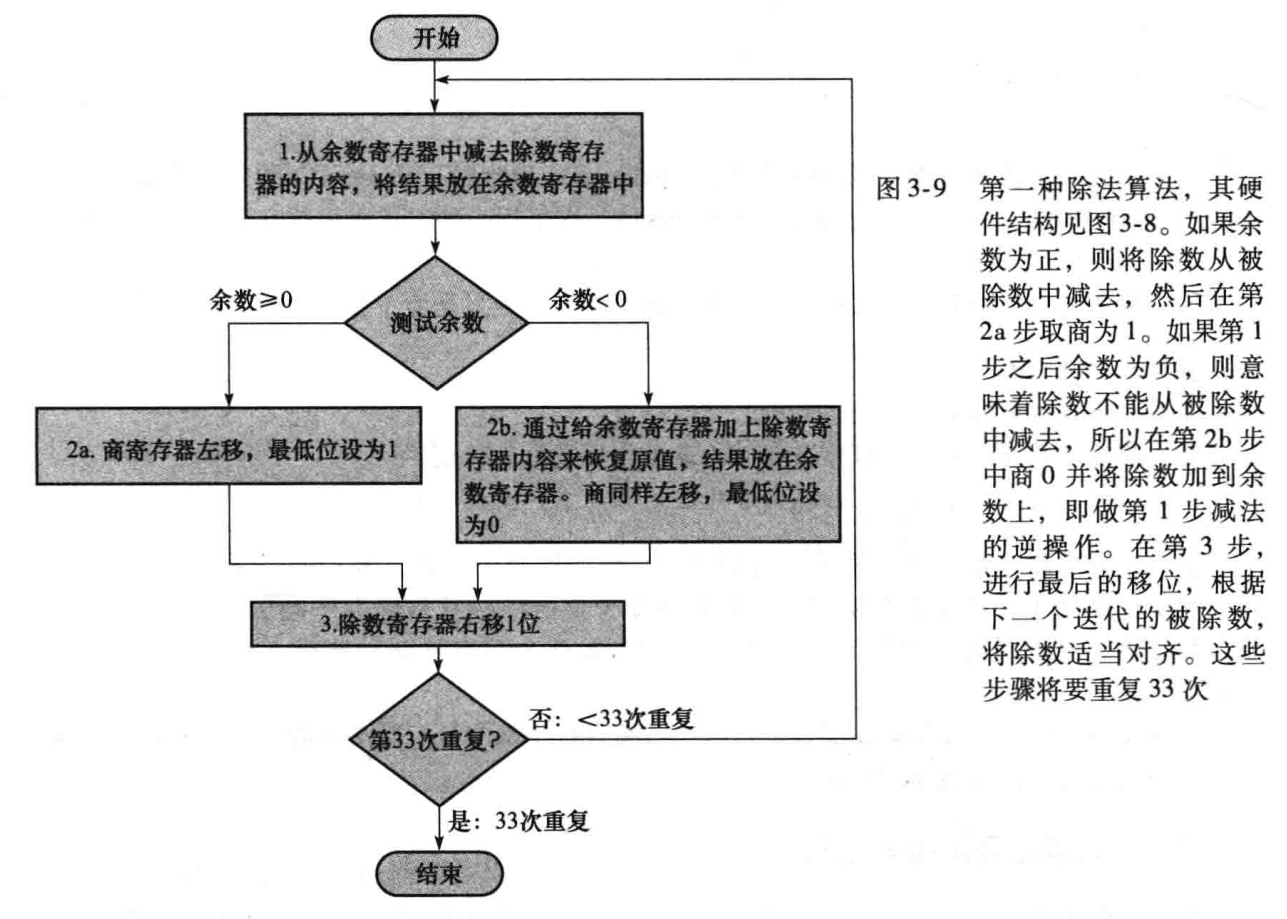
- 初始化,被除数放在一个64位寄存器里的右半边,除数放在另一个64位寄存器的左半边,商用一个32位寄存器初始为0
- 左移商
- 尝试用余数减去除数
- 若非负,商的最低为赋值为 1
- 若为负,给余数加回除数,商的最低为赋值为 0
左移商(得先左移,再赋值,否则结果相当于乘以 2 )- 右移除数
- 判断是否第33次重复
- 是则结束
- 否则回到第 2 步
判断 33 次可以理解为 1 + 32,因为除数没右移时也要尝试一次减法,而右移 32 位每次都要尝试一次减法。
改进
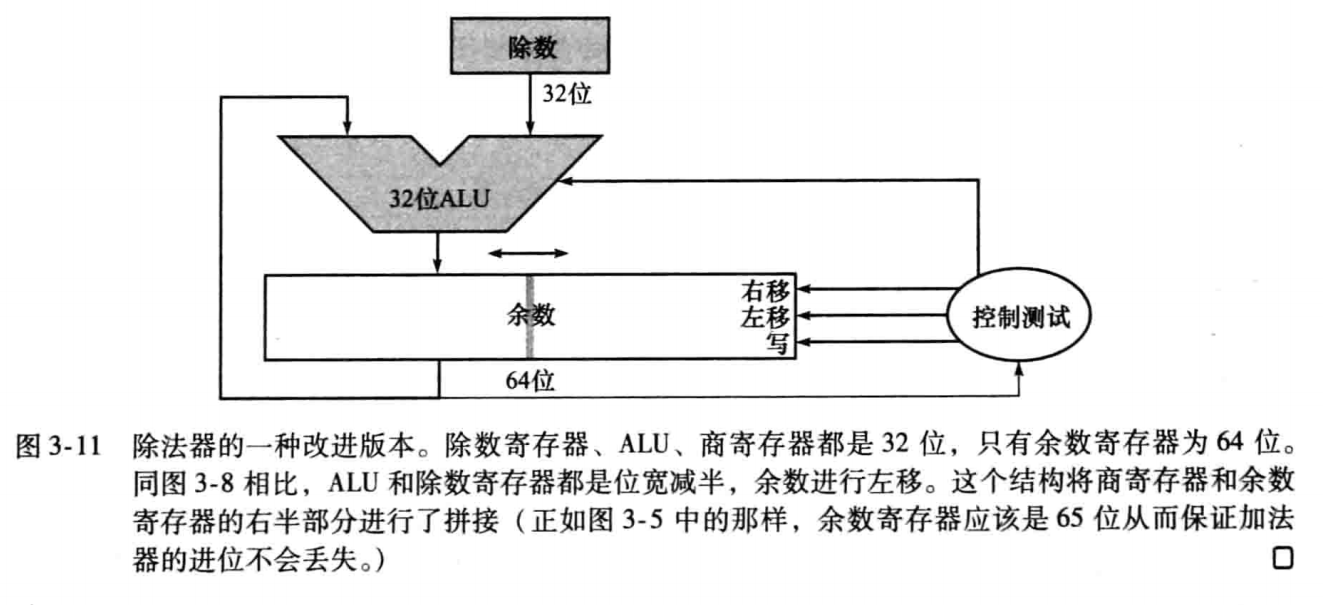
3.5 浮点运算
3.5.1 浮点表示
小数的二进制表示
回顾一下小数的二进制表示。
二进制小数 to 小数
和整数形式上是一致的
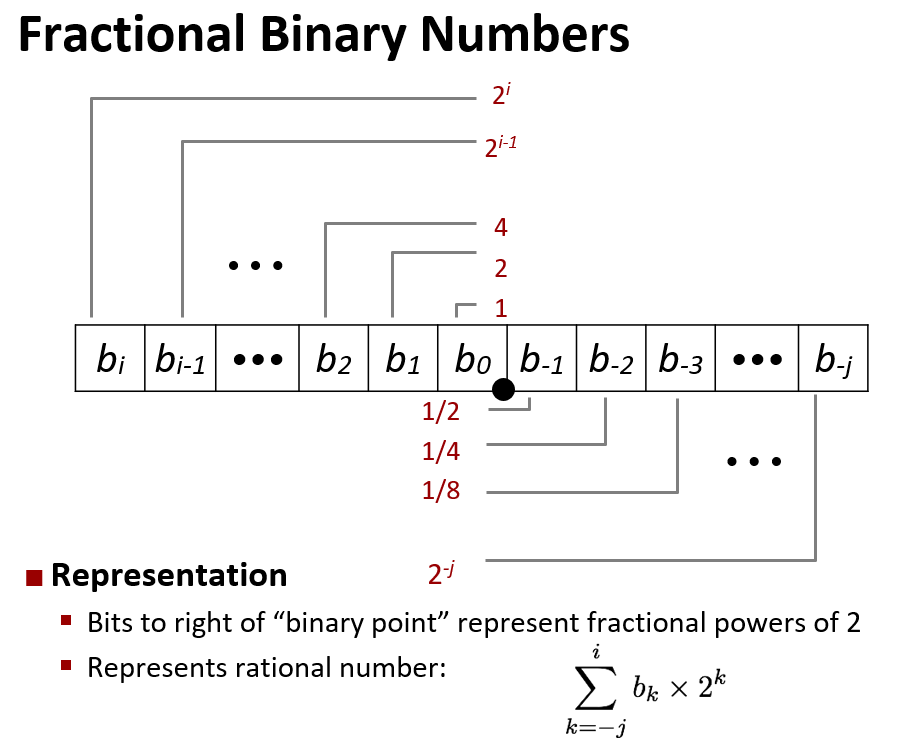
小数 to 二进制
首先可以尝试观察法:把小数表示为带分数,结合移位的知识进行表示,如
| Value | Representation |
|---|---|
| \(5\frac{3}{4}\) | \(101.11_2\) |
| \(2\frac{8}{7}\) | \(10.111_2\) |
| \(1\frac{7}{16}\) | \(1.0111\) |
另一种方法是令小数部分不断乘以 2,依次取个位,即为小数点后的位数,如图

科学计数法与规格化
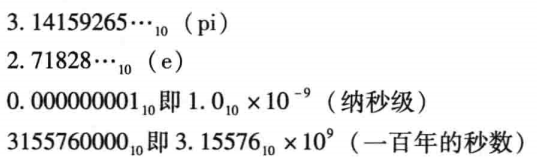
科学记数法:小数点左边只有一位整数的记数法
一个采用科学记数法表示的数,若没有前导 0 且小数点左边只有一位整数,则可称为规格化 (normalized)。
二进制的科学计数法类似十进制,只是基数从10变成了2.
| Value | Representation | Scientific Notation |
|---|---|---|
| \(5\frac{3}{4}\) | \(101.11_2\) | \(1.0111 * 2^2\) |
| \(2\frac{8}{7}\) | \(10.111_2\) | \(1.0111*2^1\) |
| \(1\frac{7}{16}\) | \(1.0111\) | \(1.0111 * 2^0\) |
注:指数在计算机中也是以二进制存储的,这里仅为简化而用十进制
IEEE Floating Point(IEEE 754)
浮点数的表示类似于上述科学计数法:
\(s\) 用来确定符号;
\(M\) 表示 \(fraction\) 或 \(significand\) ;
\(E\) 表示 \(exponent\)

在计算机中的表示
如图所示。
float

double
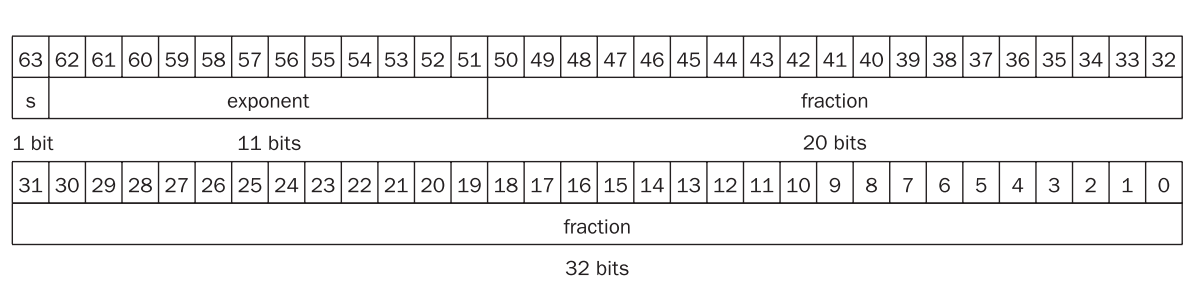
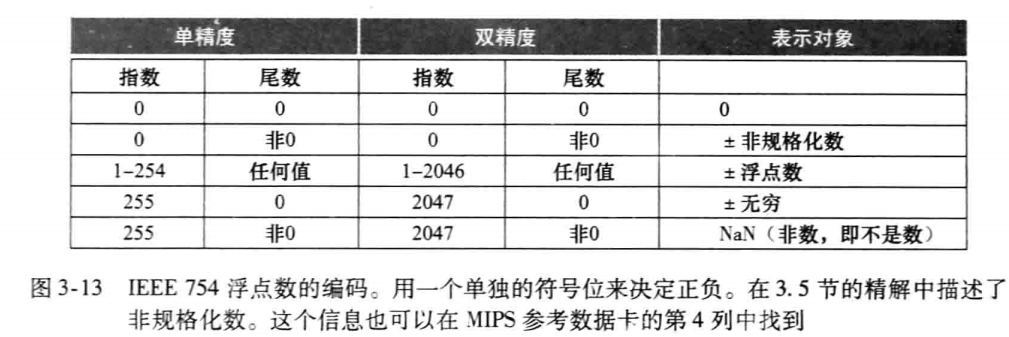
其中s和exponent直接对应了s和E,但是fraction到F要根据指数是否为 0 分类处理。
根据指数的不同,浮点数可分为三类

Case 1: Normalized Values
-
条件:\(exp ≠ 000…0 \and exp ≠ 111…1\)
-
结果:
-
指数为偏阶表示:Exponent coded as a biased value: E = Exp – Bias
-
规格化二进制数的前导位 1 会被隐藏 :Significand coded with implied leading 1: M = \(1.xxx…x_2\)
- The significand is defined to be \(M = 1 + f\) .
- \(xxx…x\): bits of frac field
- Minimum when \(frac=000…0 (M = 1.0)\)
- Maximum when \(frac=111…1 (M = 2.0 – ε)\)
- Get extra leading bit for “free”
-
Case 2: Denormalized Values
-
条件:\(exp = 000...0\)
-
结果:
-
the exponent value is E = 1 − Bias
-
the significand value is M = f
-
that is, the value of the fraction field without an implied leading 1
-
-
例子(float):

-
作用:
-
表示正负零
-
表示趋近 0 的数
-
-
和Normalized Values的联系:
- 最大的非规格化数是最小的规格化数
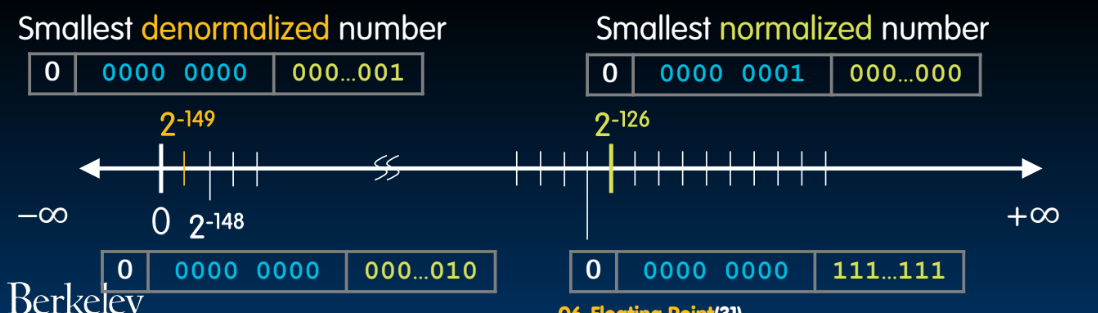
Case 3: Special Values
Biased exponent fields 0 and 255 accommodate overflow, underflow, and arithmetic errors.
浮点数能表示的范围有限,在这之外即溢出。


正负无穷
出于数学上的考虑,一个数除以 0 时会得到正负无穷。
表示: \(exp = 111..11_2, f = 000..00_2\),符号位表示正负
NaN
数学中不符合定义的一些计算结果会得到NaN,如负数开方。
表示: \(exp = 111..11_2, f = nonzero\)
总结
IEEE 754:
- 对于规格化二进制数,隐藏前导位 1.
- 对于非规格化的二进制数,令指数位为 0,指数为\((1 - bias)\),表示接近 0 的数
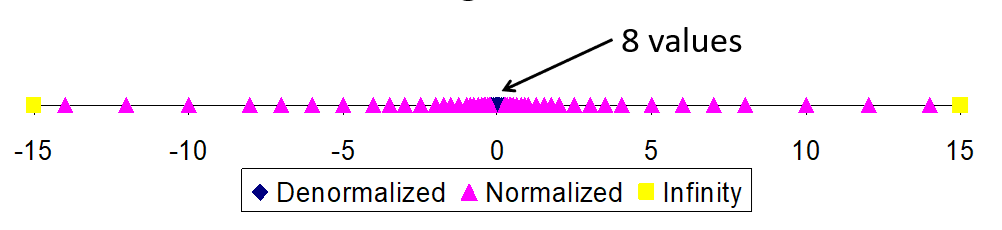
- 用特殊的符号来表示异常事件
- 将最小的负指数表示为 \(00...00_2\) 而最大的正指数表示为\(1111_2\)。称为带偏阶的记数法(biased notation)。需要从带偏阶的指数中减去偏阶,才能获得真实的值
3.5.2 浮点加法
步骤
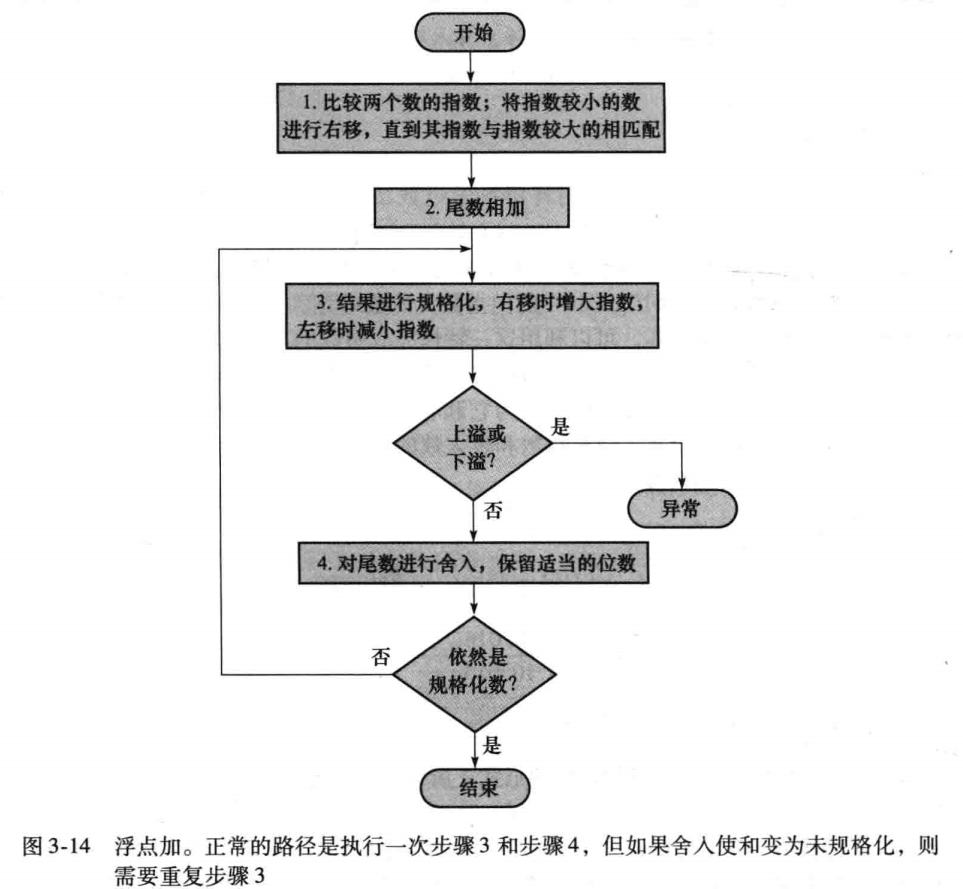
- 指数匹配,小的要匹配上大的
- 有效位数相加
- 规格化
- 检查溢出(检查指数)
- 舍入并检查是否规格化,是则结束,否则跳转至 3
例题


3.5.3 浮点乘法
步骤
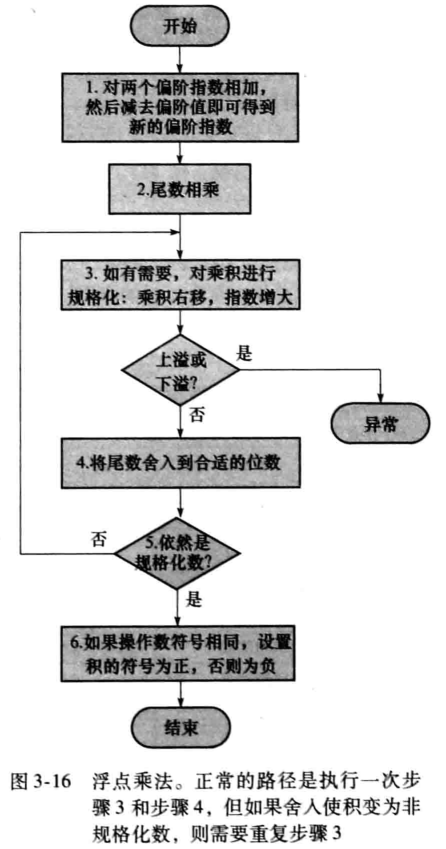
例题
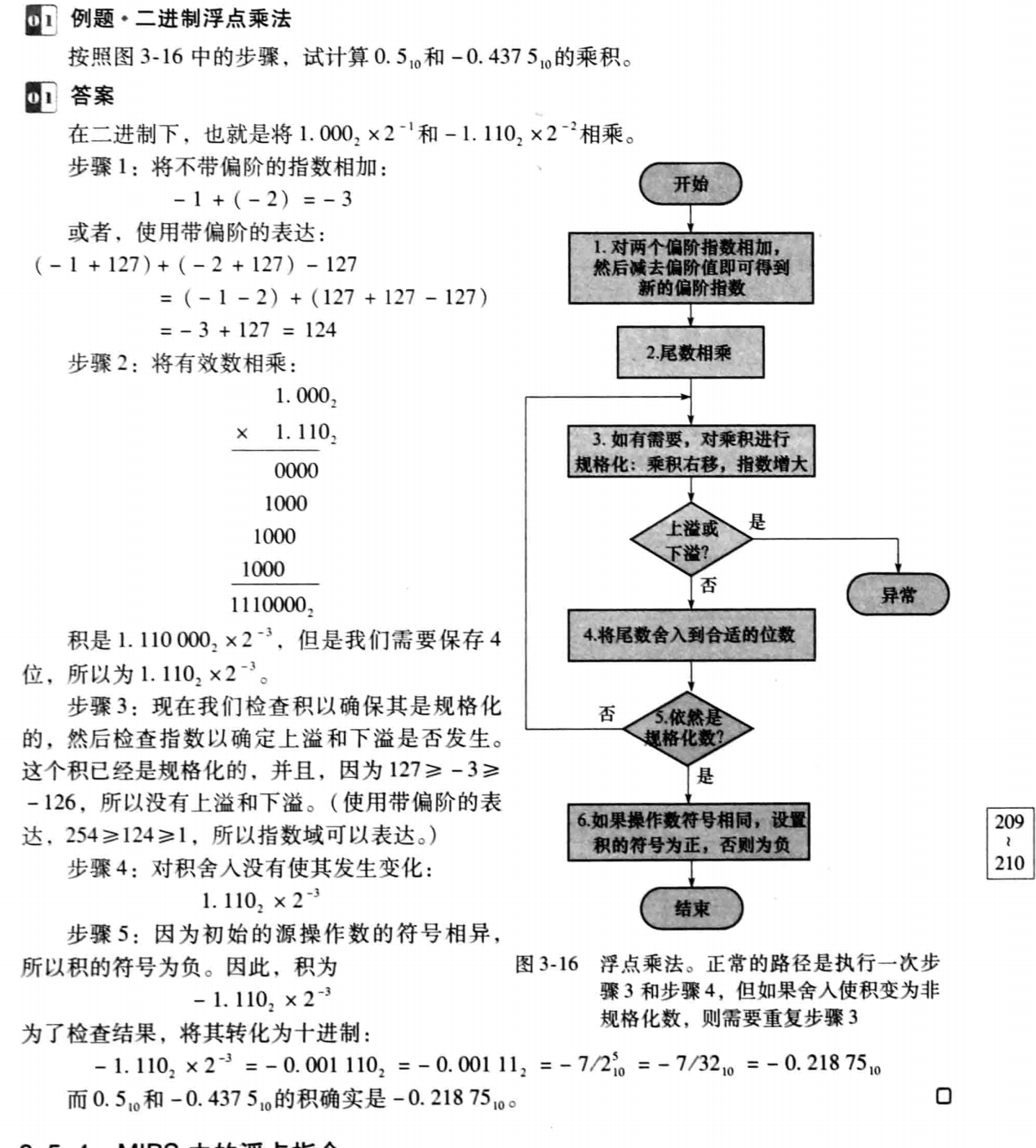
浮点数运算需要的检查
1. 检查溢出
即检查指数是否在对应的表示范围内,需要在小数规格化之后进行,以float为例,exp的范围应该是
若加上偏阶,则为
若计算后指数不在这个范围,则表示溢出。
p.s: \(exp'= 0\)和\(exp'=255\)被用于表示特殊情况(见上文)
另外在此条件下的最大最小值为:

2. 检查规格化
即检查小数点左边是否只有一位整数,需要在对小数舍入之后进行。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号