【数编】【题记】Running Median 对顶堆、链表
POJ 3784 Running Median 对顶堆、双向链表
法一:维护第\(K\)个数模型,对顶堆
核心思想:维护一对顶堆,使得大根堆和小根堆的大小相等。
 原理:
原理:
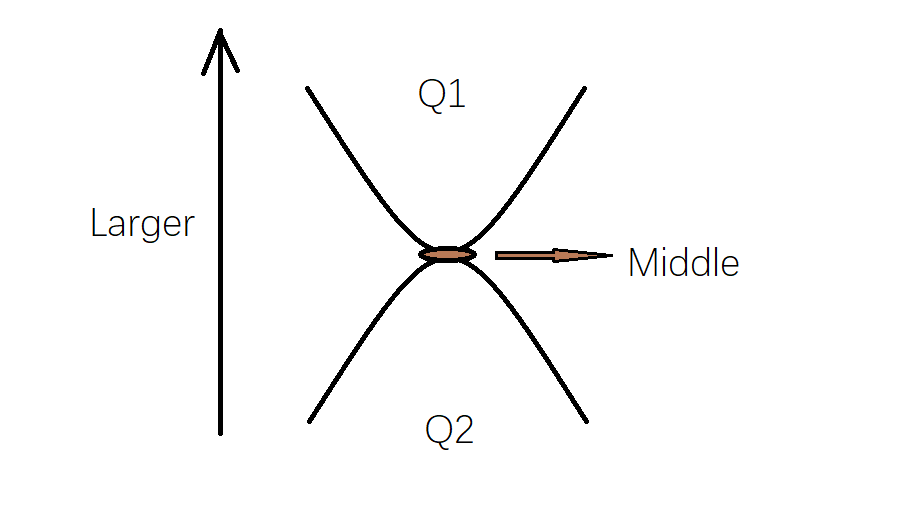
对顶堆中,小根堆的堆顶大于大根堆的堆顶,即小根堆中的所有元素都大于大根堆。
如上图所示,上方为小根堆,维护较大部分的最小值;下方为大根堆,维护较小部分的最大值。
乱序输入\(N\)个数,前\(K\)个数直接加入大根堆。从第\(K + 1\)个元素开始,对于每个元素\(x\),如果它比大根堆的堆顶大,则加入小根堆;反之将其加入大根堆,并将大根堆堆顶弹出加入小根堆。
不妨设大根堆的堆顶元素为\(\alpha\)。显然,如果\(x > \alpha\),则其不影响\(\alpha\)作为第\(K\)大的数,加入小根堆;如果\(x < \alpha\),则\(\alpha\)应该则成为第\(K + 1\)大的数,此时应该将\(x\)加入大根堆,重新生成大根堆堆顶,此时新的堆顶才是第\(K\)大的数。
应用(于此题):
上述的\(K\),其实是一个固定的\(K\),但是在本题中,我们要维护的中位数的绝对位置并不固定,因此需要对上述方法进行一定改变。
个人感觉,对顶堆的核心思想,是分别维护一串序列的较小部分最大值,较大部分的最小值,而维护的核心,就是“较大”,“较小”的分界,我们需要想办法将这个边界和对顶堆的实现对应起来。
对于固定的第\(K\)小,我们控制大根堆的大小,把较小的\(K\)个数存放在大根堆中,堆顶即所求。
对于中位数,虽然会动,但有个不变的特点就是其左右元素个数相同(本题限定只求长度为奇数的序列的中位数),对应到堆顶堆上就是两堆大小相同。
因此我们的做法就是:对于新插入的数,与中位数(大根堆堆顶)比较决定插入哪个堆中,插入之后维护一下两个堆的大小(如果一个堆的元素比另一个多\(2\),则将堆顶弹出压入另一个)。
代码
// Problem: Running Median
// Contest: Virtual Judge - POJ
// URL: https://vjudge.net/problem/POJ-3784
// Memory Limit: 64 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
const int N = 100010;
priority_queue <int,vector<int>,greater<int> > L; // 小根堆对应的是greater
priority_queue <int,vector<int>,less<int> > G; // 大根堆对应的是 less
/*
维护一对大小相差不超过 1 的对顶堆(具体而言,大根堆的大小比小根堆大0/1)。
1. 若比大根堆堆顶小,压入大根堆;否则压入小根堆
2. 若小根堆的元素比大根堆的元素多 1,则弹出堆顶压入大根堆中。
*/
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int n;
cin >> n;
while (n -- ) {
int cnt, num;
cin >> cnt >> num;
cout << cnt << " " << (num + 1 >> 1) << endl;
while (!L.empty()) L.pop();
while (!G.empty()) G.pop();
for (int i = 0; i < num; i ++ ) {
int x;
cin >> x;
// 1. 若比大根堆堆顶小,压入大根堆;否则压入小根堆
if (G.empty() || x < G.top()) {
G.push(x);
}
else {
L.push(x);
}
// 2. 若小根堆的元素比大根堆的元素多 1,则弹出堆顶压入大根堆中。
if (L.size() > G.size()) {
G.push(L.top());
L.pop();
}
else if (G.size() > L.size() + 1) {
L.push(G.top());
G.pop();
}
// 序号为奇数时,也就是 i 为偶数时输出中位数。
if (i % 2 == 0) cout << G.top() << " ";
// 格式要求
if ((i + 1) % 20 == 0) cout << endl ;
}
cout << endl;
}
return 0;
}
法二:维护中位数时,对顶堆的另一种用法
做法:
每次输入同时压入大、小根堆,需要访问中位数时,只要两个堆的堆顶元素不相等,我们就将大根堆的堆顶弹出压入小根堆,小根堆的堆顶弹出压入大根堆,相当于每次去掉一对最大最小值,向中位数逼近。
代码
参见:POJ 3784 Running Median - Seaway-Fu - 博客园
法三:双向链表
法二提到,每次删除最大最小值,向中位数逼近,在法三中,我们也使用类似的删除操作,将完整的序列进行排序,构建一个列表,记录每个节点的原始位置,每次删除输入时间较晚的两个数,并维护中位数的节点位置。
参见《数据结构编程实验》p154

代码
静态链表
#include <algorithm>
#include <iostream>
#define N 10005
using namespace std;
struct Node
{ //链节点为结构体类型
int val, pre, nxt; //数值域、前驱指针和后继指针
} node[N]; //双向链表
struct Text
{ //序列节点为结构体类型
int x, id; //数值域和输入顺序
} c[N]; //输入序列
int ans[N], a[N], d[N], T, Case, n; //中间值序列 ans[]
bool cmp(Text aa, Text bb)
{ //比较函数:以大小为第一关键字、输入顺序为第二关键字
if (aa.x != bb.x)
return aa.x < bb.x;
return aa.id < bb.id;
}
int main()
{
scanf("%d", &T); //输入测试用例数
while (T--)
{
scanf("%d %d", &Case, &n); //输入测试用例编号和待处理的有符号整数的个数
memset(node, 0, sizeof(node));
for (int i = 1; i <= n; i++)
{ //输入每个有符号整数
scanf("%d", &c[i].x);
c[i].id = i; //记下输入顺序
}
sort(c + 1, c + n + 1, cmp); //以大小为第一关键字、输入顺序为第二关键字递增排序 c[]
for (int i = 1; i <= n; i++)
{ //构造双向链表 node[]
node[i].val = c[i].x; //设置数值域、前驱指针和后继指针
node[i].pre = i - 1;
node[i].nxt = i + 1;
d[c[i].id] = i; //第 j 个输入的有符号整数为第 d[j]个大
}
node[n + 1].pre = n; //增设一个前驱指针指向 n 的链节点
int cnt = 0, x = n / 2 + 1; //中间值序列的元素个数 cnt 初始化;计算 n 是奇数时中位数的顺序 x
if (n % 2 == 0)
{ //若 n 为偶数,则记下最后一个数的大小顺序 y,删除 node[] 链中的第 y 个数
int y = d[n];
node[node[y].pre].nxt = node[y].nxt;
node[node[y].nxt].pre = node[y].pre;
n--; //元素个数 n-1,重新计算中位数顺序 x
x = n / 2 + 1;
if (x >= y)
x++; //若被删数不大于中位数,则中位数右移一个位置
}
ans[++cnt] = node[x].val; // node 序列中第 x 个节点的数值进入中间值序列 ans[]
for (int i = n; i > 1; i -= 2)
{ //从最后输入的整数出发,倒序处理
int y = d[i]; //倒数第 i 个输入的整数大小顺序为 y
node[node[y].pre].nxt = node[y].nxt; //在链表 node[]中删除第 y 个节点
node[node[y].nxt].pre = node[y].pre;
int z = d[i - 1]; //倒数第 i-1 个输入的整数大小顺序为 z
node[node[z].pre].nxt = node[z].nxt; //在链表 node[]中删除第 z 个节点
node[node[z].nxt].pre = node[z].pre;
// 调整中位数的顺序 x:若 node[]中两个被删节点都位于原中位数后,则原中位数的前驱节
// 点调整为中位数;否则若其中一个被删节点是原中位数,另一个被删节点位于其后面,则原
// 中位数的前驱节点调整为中位数;否则若 node[] 中两个被删节点都位于原中位数前,则原中
// 位数的后继节点调整为中位数;否则若其中一个被删节点是原中位数,另一个被删节点位于
// 其前面,则原中位数的后继节点调整为中位数
if (y > x && z > x)
x = node[x].pre;
else if (y > x && z == x || y == x && z > x)
x = node[x].pre;
else if (y < x && z < x)
x = node[x].nxt;
else if (y < x && z == x || y == x && z < x)
x = node[x].nxt;
ans[++cnt] = node[x].val; //调整后的中位数值进入中间值序列 ans[]
}
printf("%d %d\n", Case, cnt); //输出用例编号和中间值个数
for (int i = cnt; i >= 1; i--)
{ //按照 10 个数一行的要求,倒序输出 ans[]
if ((cnt - i + 1) % 10 == 0)
printf("%d\n", ans[i]);
else
printf("%d ", ans[i]);
}
if (cnt % 10 != 0)
printf("\n");
}
return 0;
}
动态链表
// Problem: Running Median
// Contest: Virtual Judge - POJ
// URL: https://vjudge.net/problem/POJ-3784
// Memory Limit: 64 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio>
#include <stack>
using namespace std;
const int N = 100010;
/* 链表中的元素类型 */
typedef struct
{
int val; // 值
int id; // 输入次序,从 1 开始
} elemType;
/* 定义一个链表 */
typedef struct LNode
{
elemType data;
LNode *pre;
LNode *next;
} LNode, *linkList;
// 以下三个为辅助数组,下标均为 1 开始
/* 存储排序后的元素;Nodes[i]代表第i大的元素值及其对应输入次序 */
elemType Nodes[N];
/* id-LNode映射:给定某元素为第i个输入,获取其对应在链表的节点的指针 */
LNode *addr[N];
/* id-Nodes映射:给定某元素为第i个输入,获取它在排序后的数组(Nodes)中的位置 */
int id2loc[N];
bool cmp(elemType aa, elemType bb)
{ //比较函数:以大小为第一关键字、输入顺序为第二关键字
if (aa.val != bb.val)
return aa.val < bb.val;
return aa.id < bb.id;
}
/* 尾插法新建链表 */
void tailInit(linkList &L, int num)
{
L = new LNode;
L->data.val = 0x3f3f3f3f;
L->data.id = 0;
L->next = NULL;
L->pre = NULL;
// s 指向待插入元素
LNode *s;
// r为尾指针
LNode *r = L;
for (int i = 1; i <= num; i++)
{
int x;
scanf("%d", &x);
Nodes[i].val = x;
Nodes[i].id = i;
}
//! 排序,注意此时下标从 1 开始
sort(Nodes + 1, Nodes + num + 1, cmp);
for (int i = 1; i <= num; i++)
{
id2loc[Nodes[i].id] = i;
}
/* 尾插法的核心步骤
1. 新建待插入节点
2. 令尾指针指向的节点指向新节点
3. 令尾指针指向新节点
辨析:r 是指针,可以直接操作最后一个元素,直接r->data, r->next即可
完整写法应该是(*r).data, (*r).next
*/
for (int i = 1; i <= num; i++)
{
s = new LNode;
s->data = Nodes[i];
s->pre = r;
s->next = NULL;
addr[s->data.id] = s;
r->next = s;
r = s;
}
}
/* 删除链表中输入时第 id 个输入的节点,返回这个节点在排序好的数组Nodes里的位置
1. 获取节点指针toDelete
2. 令*toDelete指向的上一个节点指向*toDelete的下一个节点
3. 如果*toDelete不是最后一个节点,则令*toDelete指向的下一个节点指向*toDelete的上一个节点
*/
int removeNode(linkList &L, int id)
{
LNode *toDelete = addr[id];
toDelete->pre->next = toDelete->next;
if (toDelete->next != NULL)
toDelete->next->pre = toDelete->pre;
delete toDelete;
return id2loc[id];
}
int main(void)
{
int n;
scanf("%d", &n);
while (n--)
{
// 双向链表
linkList L;
// 存储答案,用栈便于倒序输出
stack<int> Q;
// 题目的两个输入
int cnt, num;
cin >> cnt >> num;
tailInit(L, num);
// posM 维护中位数在排序之后的数组(Nodes)中的位置
int posM = num + 1 >> 1;
printf("%d %d\n", cnt, num + 1 >> 1);
// 由于之后要两两删除链表元素,要保证num为奇数
if (num % 2 == 0)
{
int p = removeNode(L, num); // 删最后输入的元素,肯定不是中位数
if (p <= posM)
posM++;
num--;
}
Q.push(Nodes[posM].val);
// 核心:动态删除元素并维护中位数的位置
for (int i = num; i != 1; i -= 2)
{
// 待删除的两个节点
LNode *a = addr[i], *b = addr[i - 1];
int posA = id2loc[a->data.id];
int posB = id2loc[b->data.id];
// 情况 1:中位数位置向前
if ((posA > posM && posB > posM) || (posA > posM && posB == posM) || (posB > posM && posA == posM))
{
posM = id2loc[addr[Nodes[posM].id]->pre->data.id];
}
// 情况 2:中位数位置向后
if ((posA < posM && posB < posM) || (posA < posM && posB == posM) || (posB < posM && posA == posM))
{
posM = id2loc[addr[Nodes[posM].id]->next->data.id];
}
// 其它情况中位数位置不变
// 删除节点
removeNode(L, a->data.id);
removeNode(L, b->data.id);
// 压入答案
Q.push(Nodes[posM].val);
}
// 输出答案
int t = 0;
while (!Q.empty())
{
printf("%d ", Q.top());
t++;
if (t % 10 == 0)
cout << endl;
Q.pop();
}
cout << endl;
}
return 0;
}
参考链接:
Running Median 优先队列_HigcMadoka的博客-CSDN博客


 浙公网安备 33010602011771号
浙公网安备 33010602011771号