遇到了一个很棘手的问题...

遇到了一个很棘手的问题...

Q3: CS61 - NAY

Difficulty: ⭐⭐⭐

Part A: Implement cs61nay, which takes a two argument function combiner and positive integer n and returns a function.

The returned function then takes n arguments, one at a time, and computes combiner(...(combiner(combiner(arg1, arg2), arg3)...), arg_n). Notice combiner takes in two integers and returns one integer.

For example, the first doctest has the returned function f = cs61nay(lambda x, y: x * y, 3). Now when f is applied to three arguments, like f(2)(3)(4), it multiplies them together, 2*3*4 to get 24.

IMPORTANT: For this problem, the starter code template is just a suggestion. You are welcome to add/delete/modify the starter code template, or even write your own solution that doesn’t use the starter code at all.

HINT: For the n = 1 case, the returned function doesn't use combiner.

这道题初看简单，具体做起来并不容易...

以往做类似的题，我的思路大概是用一个值去乘以另一个函数值，直到边界情况，如经典的计算阶乘

def factorio(x):
    if x == 1:
        return 1;
    else:
        return x * factorio(x - 1)

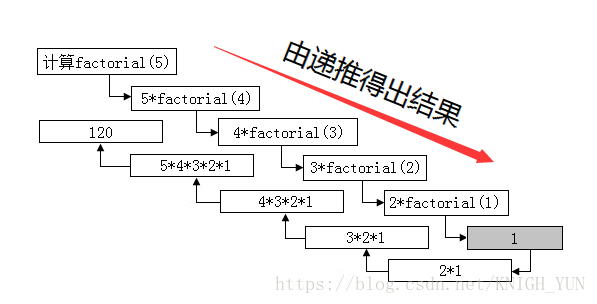
于是对于这题，我也想使用类似的思路，可是却找不出类似factorial(n - 1)这样的项，可能是因为我们开始有n个参数，接下来就应该有n-1个参数，难以简单的表示成一个函数的调用。

我的一个失败的尝试

def cs61nay(combiner, n):
    """ Return a function that takes n arguments,
    one at a time, and combines them using combiner.
    """
    if n == 1:
        return lambda x: x 
    else:
        return lambda x: lambda y: combiner(x, cs61nay(combiner, n - 1)(y))

n个参数，是这道题最大的特点，也许便使得曾经的思路不再适用——我们不能显式地给出一个返回值。

于是在这里需要用另一种方式思考。

对于

>>> f = cs61nay(lambda x, y: x * y, 3)
>>> f(2)(3)(4) # 2 * 3 * 4
24

我们无法直接实现2 * f(3)(4)，也就是类似计算阶乘的思路

这里可以边计算边递归，即从前到后两两合并。这题要求我们按顺序计算，因此某种程度上也需要我们这样做。

首先计算头两个，那我们还得计算呀，这时关键的一步就是把计算结果继续作为参数

也就是把头两个元素x,y替换为combiner(x, y)，也可以说是应用结合律首先计算头两个元素

这样的好处是减少了参数个数，也就是减小了问题规模，同时还规避了参数个数未知，无法显示写出表达式等问题

这也是递归，递归地顺序计算

代码：

def cs61nay(combiner, n):
    """ Return a function that takes n arguments,
    one at a time, and combines them using combiner.
    """
    if n == 1:
        return lambda x: x 
    else:
        return lambda x: lambda y: cs61nay(combiner, n - 1)(combiner(x, y))

另外在群里也看到了另一道题（据说是邱奇数），思路也十分多元，其中方法二与本题有异曲同工之妙

Homework 2 | CS 61A Spring 2021

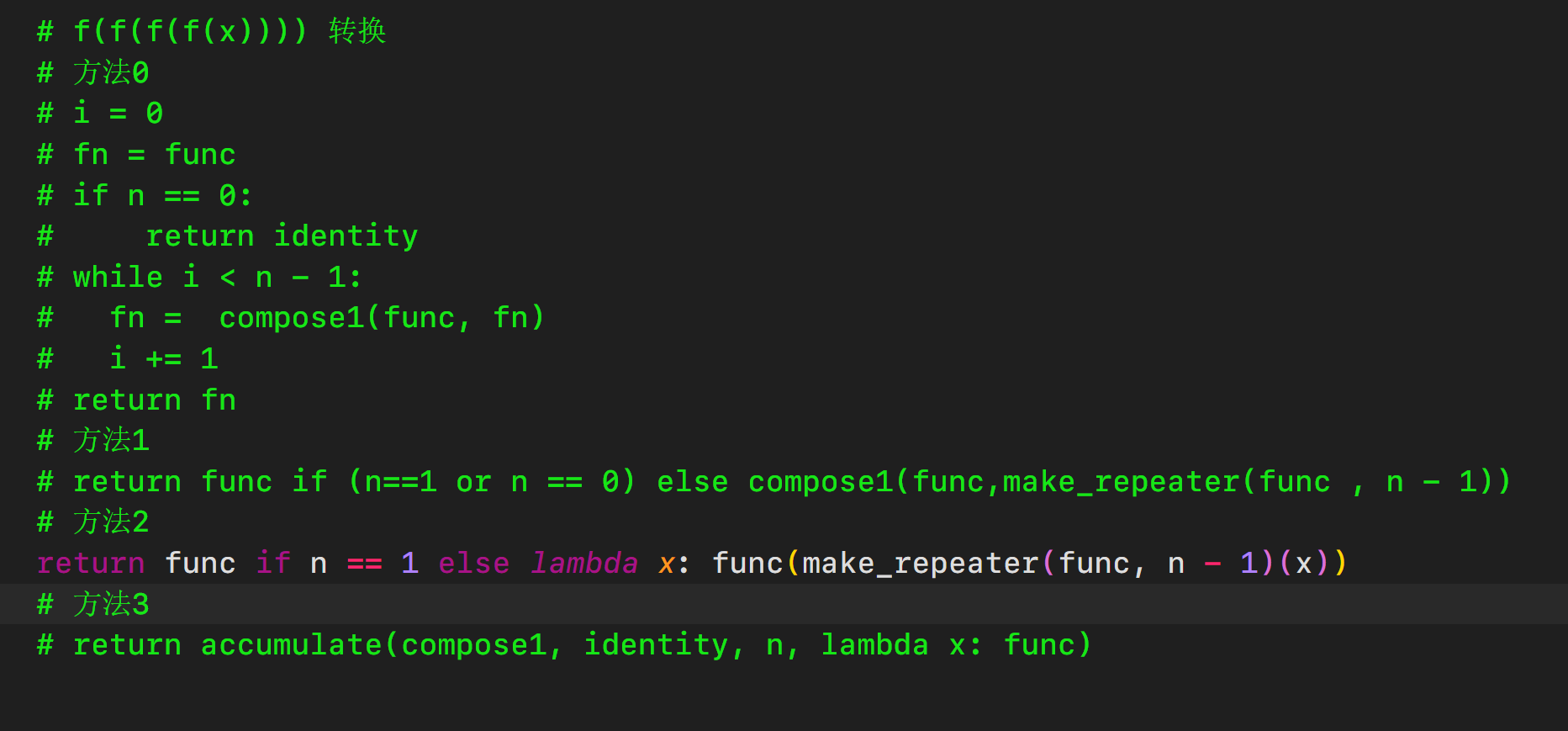
# 方法4
def make_repeater(func, n):
    """Return the function that computes the nth application of func. """
    if n == 0:
        return zero(func)
    return successor(lambda f: make_repeater(f, n - 1))(func)
    

def zero(f):
    return lambda x: x

def successor(n):
    return lambda f: lambda x: f(n(f)(x))