2014. 岛

2014. 岛

2014. 岛

模型抽象

给定数组\(a[n]\)，对于不同的整数\(k\)，求\(a[n]\)中连续的大于\(k\)的子序列的数量最大值（包括单个元素）。

在本题中，高度就相当于\(a[n]\)的值和\(k\)的值，每个\(a[n]\)中连续的大于\(k\)的子序列就是一个小岛。

模型转化

最直觉的办法就是从小到大枚举\(k\)，然后再枚举\(a[n]\)，计算“小岛”数量，不断更新答案。这样的复杂度是\(O(nk)\)的，再瞅一眼数据范围——\(1 \leq N \leq 10^5，1 \leq k \leq 10^9\)这个做法就被pass掉了。因此要循环更好的算法或者对它进行优化。

首先是\(k\)，\(k\)的范围最大，是不是都有用呢，并不是的。模拟可以发现，一些高度的变化并不会对答案产生影响，因此我们无需考虑所有没有出现的高度都无需考虑，只考虑会影响答案的高度。

数组最多只有\(10^5\)个数，因此高度最多也就只有这么多，我们至少要枚举这么多次，因此我们在计算“小岛”数量时，需要控制在\(O(\log n)\)以内。

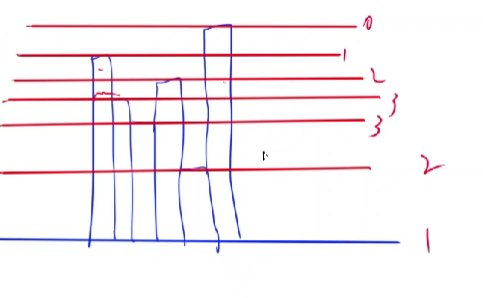
于是第二个优化就是，只考虑变化的部分。如图所示，在更新答案的时候，我们只需要关注某些发生变化的区域，就可以得到新的解，并不需要从头到尾枚举一遍。按照这样的思路，我们就可以动态的更新小岛的数量，每当枚举到一个\(k\)时，就重点关注发生变化的区域，然后更新答案。

那么如何动态更新呢？遇到这种不能一言以蔽之的情况我们就可以考虑一下分类。被水淹没，与左右相比有四种情况：

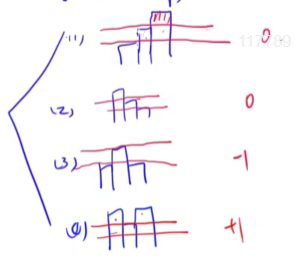
每当我们枚举了一个高度，这个高度必然对应着数组里的一个元素，我们只需要比较一下它的左右就可以更新一下答案，这样做就是\(O(n)\)的啦。

但是，我前面理想的分析其实隐约之中是蕴含了所有高度都不相等的假设的。至此我们必须考虑特殊情况——出现相等的高度。

这个特殊情况又可以分成两类，一种是相同高度相连，另一种是不相连。

首先是相同高度相连。如果我们还按照上面那种动态更新的做法，那我们必须要找到高度相连的左右边界。这就不得了了，正如yls所说，若不能确定长度，最坏情况的长度，出题人一定会出，我们不能抱有侥幸心理。

我们可以发现，这若干个连着的高度，本质上是一样的，我们要找左右边界，其实潜意识里是把这若干的连着的高度，当成了一个高度，因此我们就直接把它们当作一个高度。

也就是输入或初始化的时候，我们就把连续的相同高度合并（删去冗余只保留一个）

然后是相同高度不相连。虽然不相连的高度并不需要像上面额外判断左右边界，但它可能带来答案更新过早的问题。如图所示

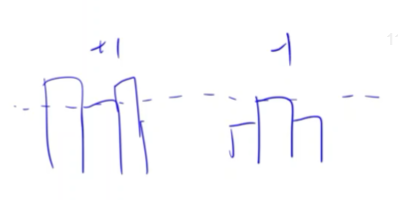
遇到这种情况，按照上面的算法，会导致答案在这一轮水面上升中更新两次，可能会导致最后我们的答案取到一个比标准答案大1甚至更多的结果。

也就是说，遇到相同高度不相连，我们不能分别更新答案。

这个问题的解决方法体现在了代码上。

其实还要考虑一种边界情况，就是最左和最右，模拟发现最左侧的左侧和最右侧的右侧设置为0，就可以得到正确答案。

代码

#include<iostream>
#include<algorithm>

#define x first
#define y second

using namespace std;

const int N = 1e5 + 10;

typedef pair<int, int> PII;

int a[N], n;
PII h[N];

int main(void){
    cin >> n;
    for (int i = 1; i <= n; i ++ ) cin >> a[i];
    n = unique(a + 1, a + n + 1) - a - 1;
    for (int i = 1; i <= n; i ++ ) h[i] = {a[i], i};    //使用h数组便于枚举，存储下标便于比较
    sort(h + 1, h + n + 1);

    int cnt = 1, ans = 1;                               //一开始就是一座小岛，所以cnt从1开始

    for (int i = 1; i <= n; i ++ ){
        auto t = h[i];
        if (a[t.y - 1]  < a[t.y] && a[t.y + 1] < a[t.y]) cnt -- ;//还有两种情况不影响答案就不写了
        if (a[t.y - 1]  > a[t.y] && a[t.y + 1] > a[t.y]) cnt ++ ;
        if(h[i].x != h[i + 1].x) ans = max(ans, cnt);   //等把相同高度的情况都算完了再更新,注意不能写i - 1
    }

    cout << ans << endl;
    return 0;
}