AcWing 1904. 奶牛慢跑

1904. 奶牛慢跑

基本条件

1. 跑道是单行道
2. N头奶牛起点不同，速度不完全相同
3. 速度慢的或相等的一定追不上速度快的
4. 速度快的一定可以追上速度慢的
5. 速度快的追上速度慢的之后，二者速度变成速度慢的

思路一：单调栈

图解

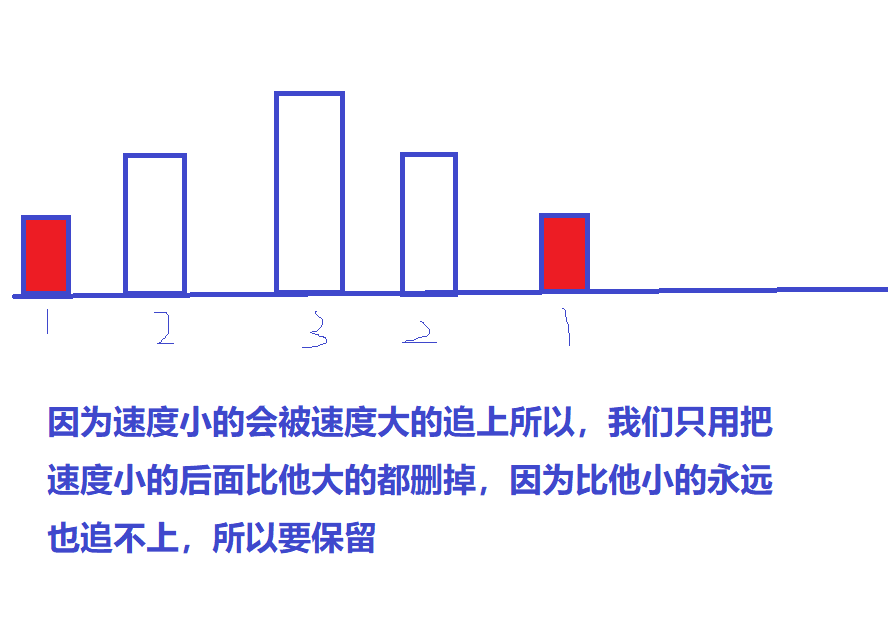
做法

\(若v_n \le v_{n + 1},则组数 + 1\)

\(若v_n \gt v_{n + 1},则v_n无效，可以替换成v_{n + 1}。然后可以迭代合并\)

最终状态一定是一个单调上升的序列

代码

#include<iostream>
using namespace std;

const int N = 100010;
int w[N];
int n;

int main(void){
    scanf("%d", &n);
    int tag = 0;
    for (int j = 1; j <= n; tag ++, j ++ ){
        int a;
        scanf("%d%d", &a, &w[tag]);
        while (w[tag] < w[tag - 1]){
            w[tag - 1] = w[tag];
            tag -- ;
        }
    }
    cout << tag << endl;
    return 0;
}

思路二：yxc法

最后所有奶牛会被分成若干个区间，每个区间有一个队长。

如何判断一头求是否为队长？———— 不会被追尾，即：

\(v_i\) 后面的牛的集合里，是否存在\(v_j\)小于\(v_i\)，即\(v_i\)后面的牛的集合的最小值是否小于\(v_i\)

做法

从后往前做，维护一个后缀最小值，每加入一个\(v_i\)就判断一下，若v[i] <= vmin,则更新答案与vmin

代码

#include<iostream>
using namespace std;

const int N = 1e5 + 10, INF = 2e9;
int n;
int w[N];

int main(void){
    scanf("%d", &n);
    for (int i = 0; i < n; i ++ ) scanf("%*d%d", &w[i]);

    int vmin = INF, ans = 0; 
    for (int i = n - 1; i >= 0; i -- ){
        if (w[i] <= vmin){
            ans ++ ;
            vmin = w[i];
        }
    }

    printf("%d", ans);
    return 0;
}