容斥原理

容斥原理

原型

求n个相交的集合的元素总个数

原理

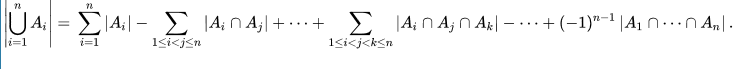
例如：

证明

设元素x在所有集合中出现了k次，然后写出等式，应用组合数恒等式

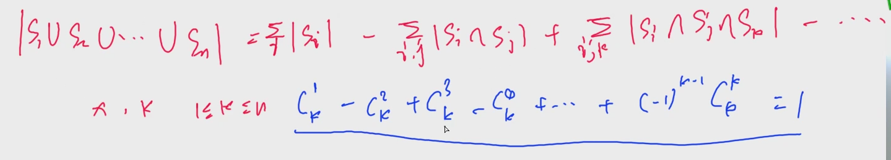
例题

给定一个整数 n 和 m 个不同的质数 p1, p2, …,pm。

请你求出 1∼n 中能被 p1, p2, …,pm 中的至少一个数整除的整数有多少个。

例子

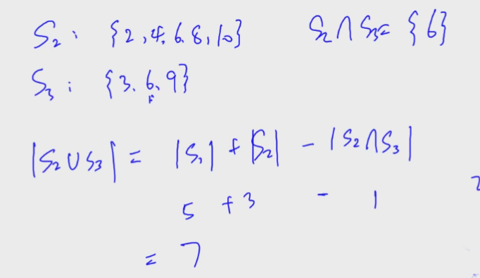
如何计算？

设\(|S_{p_i}|\)为\(1- n\)中\(p_i\)的倍数的个数，则

\[|S_{p_i}| = \lfloor \frac{n}{p_i} \rfloor \\ |S_{p1} \cap S_{p2}\cap ...\cap S_{pn}| =\lfloor \frac{n}{p_1， p_2，...p_n的最小公倍数} \rfloor \\\overset{p_i均为质数}{=} \lfloor \frac{n}{p_1 p_2...p_n} \rfloor \]

由容斥原理有

\[|S_{p_1} \cup S_{p_2} \cup ... \cup S_{p_m}|\\ = |S_{p_1}| + |S_{p_2}| + ... + |S_{p_m}| - |S_{p_1} \cap S_{p_2}| - ... + |S_{p_1} \cap S_{p_2} \cap S_{p_3} | - ...\\ = \sum _{i}|S_i| - \sum _{i,j}|S_i \cap S_j| + \sum _{i,j,k}|S_i \cap S_j \cap S_k|-... \]

这里面一共有\(2^n - 1\) 项，对应了除了全部不取以外，每个集合取或不取的所有情况

于是我们要枚举所有的选法，常用的方法是使用位运算

//枚举，从i枚举到2^n - 1
for (int i = 1; i < 1 << n; i ++ ){
    ...
}
//判断第k位是否为1
if (i >> k & 1){
    ...
}

代码

#include <iostream>
#include <algorithm>

using namespace std;

typedef long long LL;

const int N = 20;

int p[N];

int main(){
    int n, m;
    cin >> n >> m;

    for (int i = 0; i < m; i ++ ) cin >> p[i];

    int ans = 0;

    for (int i = 1; i < 1 << m; i ++ ){         //这里应把i看成二进制数，代表了一种选法的序列，代表了计算|S|的分母
        int pd = 1, cnt = 0;                    //pd（product）记录分母，若干个质数的乘积；cnt，有多少个质数，决定后面计算中是加是减
        for (int j = 0; j < m; j ++ ){          //j枚举i的第j位，i的每个第j位对应了某个集合要不要乘到分母里
            if (i >> j & 1){
                if ((LL)pd * p[j] > n){         //公式里不是所有的项都能计算，可能出现n小于某些数的乘积，故要特判。另外这里要小心爆int
                    pd = -1;
                    break;
                }
                pd *= p[j];                     //更新
                cnt ++ ;
            }
        }
        if (pd != -1){
            if (cnt % 2 == 0) ans -= n / pd;    //按照公式计算
            else ans += n / pd;
        }
    }

    cout << ans << endl;
    return 0;
}