卡特兰数

卡特兰数

模型

给定 n个 0 和 n 个 1，它们将按照某种顺序排成长度为 2n 的序列，求它们能排列成的所有序列中，能够满足任意前缀序列中 0 的个数都不少于 1 的个数的序列有多少个。

几何意义

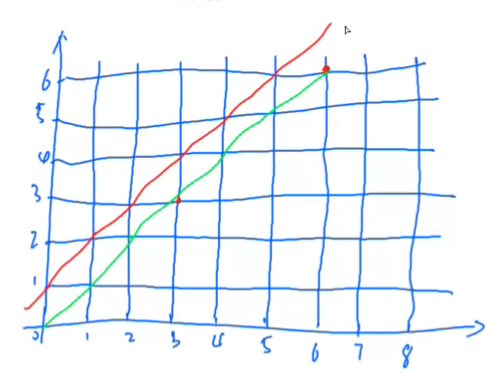
对于每一个序列，我们定义

0：向右走一格

1：向左走一格

于是每一个长度为 2n 的序列都对应了坐标系中条从\((0, 0)\)走到\((n, n)\) 的路径

而所谓“任意前缀序列中 0 的个数都不少于 1 的个数”的几何意就是这些路径不能经过红色的点

于是我们所要求的序列就是，不经过红色点的，从\((0, 0)\)走到\((n, n)\) 的路径的数量

如何求？

正难则反——转换为，求“从\((0, 0)\)走到\((n, n)\) 的所有路径”的数量与“经过红色点的，从\((0, 0)\)走到\((n, n)\) 的路径"的数量的差。

从\((0, 0)\)走到\((n, n)\) 的所有路径”的数量

\[C_{2n}^{n} \]

经过红色点的，从\((0, 0)\)走到\((n, n)\) 的路径"的数量

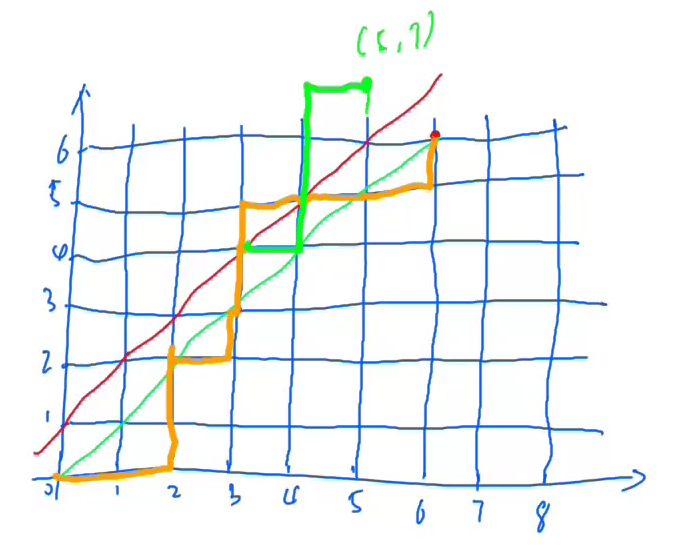
对于每一条这样的路径，我们总可以将第一个经过红色点的路径沿\(y = x\)翻折，于是所求就转换成了从\((0, 0)\)到\((n - 1, n + 1)\)的路径数量，类似于零点存在定理，这样的路径一定会经过红色的点，所以答案就是\(C^{n - 1}_{2n}\)

结论

于是不经过红色点的，从\((0, 0)\)走到\((n, n)\) 的路径的数量就是

\[C^{n}_{2n} - C^{n-1}_{2n} = \frac{1}{n + 1} C^{n}_{2n}\\ = \frac{2n (2n - 1)...(n+1)}{(n + 1)n !} \\ = \frac{2n (2n - 1)...n}{n !} \]

代码

#include<iostream>
using namespace std;

typedef long long ll;

const int mod = 1e9 + 7;

int qmi(int a, int k, int p){
    int ans = 1;
    while (k){
        if (k & 1) ans = (ll) ans * a % p;
        a = (ll)a * a % p;
        k >>= 1;
    }
    return ans;
}

int main(void){
    int n;
    cin >> n;

    int a = n * 2, b = n;
    int ans = 1;
    //求Ca-b
    for (int i = a; i > a - b; i -- ) ans = (ll)ans * i % mod;
    for (int i = 1; i <= b; i ++ ) ans = (ll)ans * qmi(i, mod - 2, mod) % mod;
    //还有一个系数1 / (n + 1)
    ans = (ll)ans * qmi(n + 1, mod - 2, mod) % mod;

    cout << ans;

    return 0;
}