支持向量机(SVM)
支持向量机是一种分类模型。模型认为,离分类超平面越远的点,判定结果越准确,所以模型的训练目标就是让离分类超平面最近的样本点距离最大。我们先从最基本的线性可分支持向量机(硬间隔支持向量机)开始推导,之后再推广到可以容纳一定误分类点的线性支持向量机(软间隔支持向量机),最后介绍核函数与 SMO 算法。
支持向量机解决的问题
假设我们正在进行一个二分类问题,并且已经画好了一条分类线。如下图,现在我们有 3 个点(ABC)等待判断。
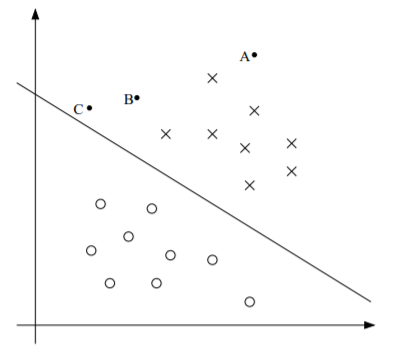
虽然按照我们的分类线,这 3 个点都应该属于 X 类。可是 A 点离分类线最远,应该来说我们将它分为 X 类的把握最大;而 C 点离分类线很近,万一分类线出现了一些偏差,C 点的判定结果可能就改变了,这样说来我们将它分为 X 类的把握最小;而 B 点位于 AC 两点中间,分类正确的把握也位于 AC 之间。
这样看来,一个点离分类超平面越远,该点就越不容易因为分类超平面的误差而被误判,我们对该点的分类结果也就越稳定。如果我们能尽量增大样本点到分类超平面的距离,是不是就能尽量增大训练样本正确分类的把握呢?
支持向量机就是来解决这个问题的。支持向量机的训练目的就是找到一个分类超平面,使得样本点中离分类超平面最近的点距离最大。
线性可分支持向量机
接下来我们来推导线性可分支持向量机的算法。在推导过程中,我们假设存在一个超平面,能够将所有样本点正确分类。
设分类超平面为 $w^Tx+b = 0$,根据几何知识我们知道,对于样本点 $(x^{(i)},y^{(i)})$(其中 $y^{(i)} = \pm 1$ 表示两个类别),$y^{(i)}(w^Tx^{(i)}+b)$ 的值越大,则样本点距离分类超平面越远。我们称这个值为样本点的函数间隔。容易发现,函数间隔大于 0 的点就是被正确分类的点,小于 0 的点就是被错误分类的点,而等于 0 的点就是位于分类超平面上的点。
但用函数间隔作为样本点的度量是不准确的,因为只要把分类超平面变成 $kw^Tx+kb=0$,那么样本点的函数间隔就会变为原来的 $k$ 倍,而样本点距离分类超平面的远近没有任何改变。所以我们引入样本点的几何间隔 $\frac{1}{|w|}y^{(i)}(w^Tx^{(i)}+b)$ 作为度量样本点距分类超平面远近的值。由几何知识易得,几何间隔就是样本点到分类超平面的距离。
支持向量机的训练目标是最大化最小的几何间隔,我们容易写出以下目标函数:$$\max_{w,b,\gamma} \gamma \\ \text{s.t.} \quad \frac{1}{|w|}y^{(i)}(w^Tx^{(i)}+b) \ge \gamma$$ 糟糕的是,限制条件并不是凸函数,没法用凸优化的方式解决。
由于函数间隔并不影响我们的优化目标(只要对 $w$ 和 $b$ 进行缩放,就能获得任意的函数间隔),我们完全可以令最小的函数间隔等于 1。这样,最小的几何间隔就变为了 $\frac{1}{|w|}$。我们可以改写目标函数:$$\max_{w,b}\frac{1}{|w|} \\ \text{s.t.} \quad y^{(i)}(w^Tx^{(i)}+b) \ge 1$$ 最大化 $\frac{1}{|w|}$,就相当于最小化 $\frac{1}{2}|w|^2$,所以我们可以继续改写目标函数为 $$\min_{w,b}\frac{1}{2}|w|^2 \\ \text{s.t.} \quad y^{(i)}(w^Tx^{(i)}+b) \ge 1$$ 现在目标函数是凸函数,限制函数是仿射函数(也是凸函数)了。很显然,这是一个二次规划(quadratic programming)问题,我们完全可以用凸优化中解决 QP 问题的方法来求出这个函数的解。不过,针对支持向量机要优化的问题,我们还可以继续推导出一个比一般解决 QP 问题效率更高的方法。
我们利用拉格朗日对偶,将优化目标写成原问题和对偶问题的形式。
原问题:$$\min_{w,b}\max_{\alpha}\frac{1}{2}w^Tw + \sum_{i=1}^m \alpha_i(1-y^{(i)}(w^Tx^{(i)}+b)) \\ \text{s.t.} \quad \alpha_i \ge 0$$
对偶问题:$$\max_{\alpha}\min_{w,b}\frac{1}{2}w^Tw + \sum_{i=1}^m \alpha_i(1-y^{(i)}(w^Tx^{(i)}+b)) \\ \text{s.t.} \quad \alpha_i \ge 0$$
由于我们假设能正确分类所有样本点的超平面存在,所以的确有一组 $w$ 和 $b$ 使得最小的函数间隔 $y^{(i)}(w^Tx^{(i)}+b) > 0$,对 $w$ 和 $b$ 进行放缩就能保证最小的函数间隔 $y^{(i)}(w^Tx^{(i)}+b) > 1$。也就是说,这个问题满足 Slater's condition,可以利用 KKT 条件求出问题的解。
根据 KKT 条件,我们有:$$\nabla_w = w - \sum_{i=1}^m\alpha_i y^{(i)}x^{(i)} = 0 \\ \nabla_b = -\sum_{i=1}^m\alpha_i y^{(i)} = 0$$ 代入对偶问题的式子我们有:$$\max_{\alpha}-\frac{1}{2}\sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy^{(i)}y^{(j)}\langle x^{(i)},x^{(j)}\rangle + \sum_{i=1}^m\alpha_i \\ \text{s.t.} \quad \alpha_i \ge 0 \\ \sum_{i=1}^m\alpha_i y^{(i)} = 0$$ 其中 $\langle x^{(i)},x^{(j)}\rangle$ 表示点积。
我们可以通过一个较为高效的算法(稍后叙述)解决上面这个优化问题,求出 $\alpha$ 的最优值。
令 $g_i(x) = 1-y^{(i)}(w^Tx^{(i)}-b)$。由 KKT 条件可知,$\alpha_ig_i(x) = 0$。也就是说,若 $\alpha_i > 0$,必然有 $g_i(x) = 0$,即第 $i$ 个样本点是距离分类超平面最近的样本点之一,我们称这样的样本点为支持向量;对于一个不是支持向量的样本点,由于 $g_i(x) < 0$,必须要有 $\alpha_i = 0$。
求出 $\alpha$ 的值后,我们代入由 KKT 条件推出的式子,即可获得 $w$ 的值。将 $w$ 用 $\alpha$ 表示后代入分类超平面的式子,则分类超平面为 $$\sum_{i=1}^m\alpha_iy^{(i)} \langle x^{(i)},x \rangle + b = 0$$ 而对于支持向量来说,由于 $$y^{(i)}(w^Tx^{(i)}+b) = 1$$ 那么我们任意选择一个支持向量,即可算出 $$y^{(i)}b = 1 - y^{(i)}\sum_{j=1}^m\alpha_jy^{(j)} \langle x^{(j)}, x^{(i)} \rangle$$ 由于 $(y^{(i)})^2 = 1$,两边同乘 $y^{(i)}$ 有 $$b = y^{(i)} - \sum_{j=1}^m\alpha_jy^{(j)} \langle x^{(j)}, x^{(i)} \rangle$$ 我们就得到了最优的分类超平面。
线性支持向量机
在大部分情况下,数据都不是完全线性可分的,可能存在部分特例(outlier)。此时我们可以使用机器学习中的经典套路——正则化让模型容忍一定的分类错误。
引入正则化项 $\xi$ 与系数 $C$,我们将优化目标改为 $$\min_{w,b,\xi}\frac{1}{2}|w|^2 + C\sum_{i=1}^m\xi_i \\ \text{s.t.} \quad y^{(i)}(w^Tx^{(i)}+b) \ge 1 - \xi_i \\ \xi_i \ge 0$$ 直观地说,我们可以付出一定的代价 $C\xi_i$,让某些样本点的函数间隔小于 1,甚至为负(即可以容忍部分样本点的分类错误)。$C$ 就是调节模型对分类错误容忍程度的系数。
我们同样可以使用拉格朗日对偶求出这个优化问题的解。同样将问题写成原问题和对偶问题的形式。
原问题:$$\min_{w,b,\xi}\max_{\alpha,\beta}\frac{1}{2}|w|^2+C\sum_{i=1}^m\xi_i+\sum_{i=1}^m\alpha_i(1-\xi_i-y^{(i)}(w^Tx^{(i)}+b)) - \sum_{i=1}^m\beta_i\xi_i \\ \text{s.t.} \quad \alpha_i \ge 0 \quad \beta_i \ge 0$$
对偶问题:$$\max_{\alpha,\beta}\min_{w,b,\xi}\frac{1}{2}|w|^2+C\sum_{i=1}^m\xi_i+\sum_{i=1}^m\alpha_i(1-\xi_i-y^{(i)}(w^Tx^{(i)}+b)) - \sum_{i=1}^m\beta_i\xi_i \\ \text{s.t.} \quad \alpha_i \ge 0 \quad \beta_i \ge 0$$
同样容易验证这个问题满足 Slater's condition,利用 KKT 条件仍有 $$\nabla_w = w - \sum_{i=1}^m\alpha_iy^{(i)}x^{(i)} = 0 \\ \nabla_b = -\sum_{i=1}^m\alpha_iy^{(i)} = 0 \\ \nabla_{\xi_i} = C - \alpha_i - \beta_i = 0$$ 由第三个式子,再加上 $\alpha_i \ge 0$ 与 $\beta_i \ge 0$ 可以看出 $0 \le \alpha_i \le C$。将上面的式子代回对偶问题有 $$\max_{\alpha}-\frac{1}{2}\sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy^{(i)}y^{(j)}\langle x^{(i)},x^{(j)}\rangle + \sum_{i=1}^m\alpha_i \\ \text{s.t.} \quad 0 \le \alpha_i \le C \\ \sum_{i=1}^m\alpha_i y^{(i)} = 0$$ 和线性可分支持向量机所导出的问题相比,只是 $\alpha_i$ 的取值范围有所变化。
事实上,线性支持向量机还可以从经验风险最小化(ERM)的角度来解释。我们知道,各种机器学习方法事实上是从参数空间中选出一组参数,使得训练样本的“损失”最小。对于二分类问题来说,0-1 损失函数(一个分类正确时取 0,分类错误时取 1 的函数,是一个阶梯形的函数)应该是最为“公正”的损失函数。但是使用这个阶梯形函数作为损失函数来选择最优参数是一个 NP Hard 问题,所以大部分算法都会使用一个近似的损失函数进行优化。
线性支持向量机可以看作是最小化以下损失函数:$$\sum_{i=1}^m[1-y^{(i)}(w^Tx^{(i)}+b)]_+ + \lambda|w|^2$$ 其中 $$[x]_+ = \begin{cases} x & x > 0 \\ 0 & x \le 0 \end{cases}$$ 称为合页损失函数,而另外一项是正则化项。
我们只要令 $[1-y^{(i)}(w^Tx^{(i)}+b)]_+ = \xi_i$,代入损失函数就有 $$\sum_{i=1}^m\xi_i + \lambda|w|^2$$ 我们取 $\lambda = \frac{1}{2C}$,代入损失函数就有 $$\frac{1}{C}(\frac{1}{2}|w|^2 + C\sum_{i=1}^m\xi_i)$$ 这和线性支持向量机的优化目标恰好是相同的。
0-1 损失函数和合页损失函数图形如下:
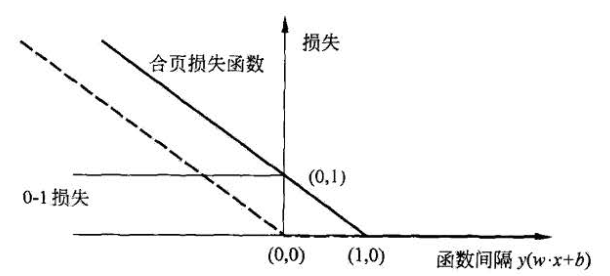
不难看出,合页损失函数是 0-1 损失函数的上限,而且合页损失函数在分类确信度足够高的时候损失才为 0,因此比 0-1 损失函数的要求更高。
核函数
虽然我们已经了解了线性支持向量机的原理,但是现实生活中的很多问题都是线性不可分的,很可能需要分类超“曲面”才能较好地把各类数据点分开。我们可能不仅需要 $x_1$,$x_2$ 这些特征,还可能需要 $x_1^2$,$x_1^3$ 或者 $x_1x_2$ 这类更高维的“组合”出来的特征。核函数就是一个运算量较少,却能获得高维特征信息的方法。
我们定义 $\phi(x)$ 为一个把原来的特征变化到更高维特征的映射。比如,把一个一维的特征变成三维的特征,我们可以定义 $\phi(x) = \begin{matrix} x & x^2 & x^3 \end{matrix}^T$。我们再定义核函数 $K(x,z) = \phi(x)^T\phi(z)$,这是一个高维特征向量的点积。我们回顾支持向量机的式子不难发现,式子中也有许多点积的部分,使用核函数时只要把核函数替换到原来点积的位置就可以了。
核函数精妙的地方,就是可以用较少的时间计算出高维特征向量的点积。例如,我们定义一个核函数为 $K(x,z) = \phi(x)^T\phi(z) = (x^Tz)^2$,展开后我们有 $$K(x,z) = (\sum_{i=1}^nx_iz_i)^2$$ $$=\sum_{i=1}^nx_iz_i\sum_{j=1}^nx_jz_j$$ $$=\sum_{i=1}^n\sum_{j=1}^n(x_ix_j)(z_iz_j)$$ 容易看出,这里的 $\phi(x)$ 是一个 $n^2$ 维的向量。如果直接计算 $\phi(x)$ 和 $\phi(z)$ 的点积,复杂度是 $O(n^2)$ 的,而使用核函数就能将复杂度降为 $O(n)$。
(据说核函数还有另一种解释,就是一个判断两条数据是否相似的函数,虽然我并不知道为什么可以这样解释...但是这种解释有助于我们在特定的应用场景下选择核函数。)
那么,给定一个核函数,是否存在一个 $\phi(x)$ 满足 $K(x,z) = \phi(x)^T\phi(z)$ 呢?考虑任意 $m$ 个可能的原始特征向量 $x^{(1)}, x^{(2)}, \dots, x^{(m)}$ (不一定是训练数据),我们定义矩阵 $M$,满足 $M_{i,j} = K(x^{(i)},x^{(j)})$。对于任意 $m$ 维向量 $z$,如果 $\phi(x)$ 的确存在,我们有 $$z^TMz = \sum_{i=1}^m\sum_{j=1}^m z_iM_{i,j}z_j \\ = \sum_{i=1}^m\sum_{j=1}^m z_i\phi(x^{(i)})^T\phi(x^{(j)})z_j \\ = \sum_{i=1}^m\sum_{j=1}^m z_i\sum_{k=1}^n\phi_k(x^{(i)})^T\phi_k(x^{(j)})z_j \\ = \sum_{k=1}^n\sum_{i=1}^m\sum_{j=1}^m z_i\phi_k(x^{(i)})^T\phi_k(x^{(j)})z_j \\ = \sum_{k=1}^n(\sum_{i=1}^mz_i\phi_k(x^{(i)}))^2 \ge 0$$ 所以 $M$ 必须对于任意一组可能的原始特征向量都为半正定矩阵。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号