分享小记：社交网络中的信息传播

第一次参加实验室的组会，实验室的史学长给大家简单分享了一个研究方向：社交网络中的信息传播，感觉讲得非常棒。这里简单记录一下这个方向的要解决的问题与解决方案。

 

社交网络中信息传播要解决的问题

社交网络中信息传播的背景就是我们所处的社交环境。包含复杂社会结构的社交网络对于信息的传播和扩散起着至关重要的作用，而基于“口碑”效应的病毒式营销受到越来越广泛的关注，社交网络上的影响力传播被日益重视。社交网络中的信息传播就将这个现象抽象成了一个问题：在一张社交网络图上，初时刻激活 $K$ 个种子节点，使得随后的时间里，随着网络的扩散效应，信息能被更多的人所知。这就是信息传播的目标：影响力最大化。

这个问题最为常用的模型称为独立级联模型（Independent Cascade Model，IC 模型）：用节点代表社交网络中的人，一条从点 A 到点 B 的、边权为 $p$ ($0 \le p \le 1$) 的有向边表示 A 知道一个信息之后，会以 $p$ 的概率告诉 B。在初始时刻，有 $K$ 个种子节点被激活（也就是说，一开始把消息告诉社交网络里的 $K$ 个人）；此后每个时刻，被激活的节点以概率 $p$ 激活其相邻的非激活节点，无论成功与否，激活动作只做一次，此后的任何时间都不再尝试。显然，当某个时刻没有新的节点被激活，那么信息传播过程结束。

下图就是 IC 模型的一个示意。红色节点代表已激活的节点，绿色节点代表未激活的节点，红色边代表激活成功的边，绿色虚线边代表激活失败的边，绿色实线边代表还没有进行尝试的边。

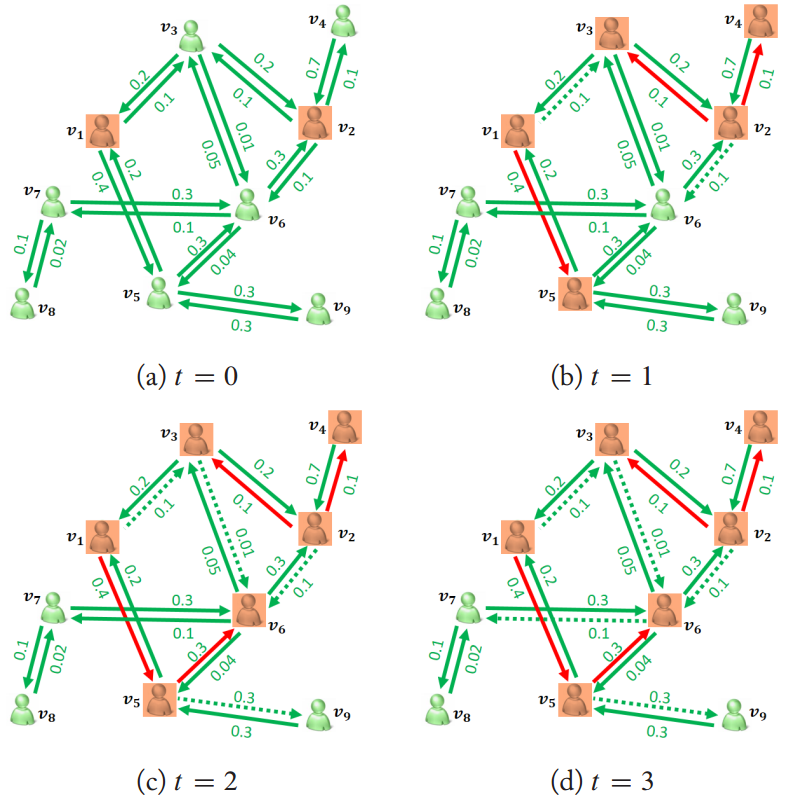
用数学公式表述，社交网络中的信息传播希望得到下面这个式子的最优解：$$\max_{S_0} \sigma(S_0) \\ \text{s.t.} \quad |S_0| \le K$$ 其中 $S_0$ 就是最开始激活的 $K$ 个种子节点，$\sigma(S_0)$ 表示以 $S_0$ 作为种子节点集时，最终激活节点数的期望。

然而这个问题并不是那么好解决的（否则也不用研究啦- -），因为这是一个 NP-Hard 问题，另一个 NP-Hard 问题 Maximum coverage problem 可以规约到 IC 模型。Maximum coverage problem 是说：给出全集 $U = \{e_1, e_2, \dots, e_n\}$，再给出一些子集 $A_1, A_2, \dots, A_m$，$A_i \subset U$（也就是说每个 $A_i$ 包含一些 $e_j$）。现在要选出 $K$ 个子集，使得它们的并集包含最多的元素。我们只要把子集 $A_i$ 和元素 $e_j$ 都看成节点，如果 $A_i$ 包含 $e_j$ 则从 $A_i$ 向 $e_j$ 连一条权值为 1 的有向边，就能把 Maximum coverage problem 看作 IC 模型的特例了。

事实上，就连计算 $\sigma(S_0)$ 也不是那么好解决的，这是一个 #P-Hard 问题。另一个 #P 问题（简单来说就是问一个 NP 问题的解有几个，或者说求方案数）S-T connectivity problem 可以规约到这个问题。S-T connectivity problem 求的是包含从 S 到 T 路径的生成子图的数量。显然，我们只要让每条边的边权都是 0.5，就能把 S-T connectivity problem 看作求 $\sigma(S_0)$ 的特例。

 

一个贪心算法

既然是 NP-Hard 问题，大家当然只能想办法去找近似解了...对于求 $\sigma$ 这个问题，比较朴实的想法就是进行大量的模拟实验（就像 IC 模型描述的一样，一开始激活选定的 $K$ 个节点，然后每个时刻进行一次激活尝试，直到没有节点被激活为止），最后取实验结果的均值。而对于影响力最大化这个问题，一个比较直接的想法就是使用贪心：循环 $K$ 次，每次枚举所有未被选为种子节点的点，计算一下它也成为种子节点后，答案的增幅有多少，把让答案增加最多的点加入种子节点集。

在 Maximizing the Spread of Influence through a Social Network 这篇文章中，作者们利用了单调子模的特性证明了这个贪心算法的近似比为 $1-\frac{1}{e}$，其中 $e$ 是自然对数的底（不过至于怎么证的我也不知道- -没有读过文章...）。单调子模指的是：设原图顶点集为 $V$，$v \in V$。若 $S \subset T \subset V$ 且 $v \notin T$，那么 $\sigma(S \cup \{v\}) - \sigma(S) \ge \sigma(T \cup \{v\}) - \sigma(T)$。这个东西具体怎么证我也不太清楚- -但是直观上来理解，初始节点越多，每增加一个新节点为最终结果带来的增幅应该越小（因为总的顶点就那么多个），这还是很有道理的- -

显然，这个算法主要的瓶颈在于对 $\sigma$ 的估计。论文中指出，设节点数为 $n$，边数为 $m$，如果通过大量模拟实验估计 $\sigma$，则以 $1-\frac{1}{n}$ 的概率获得 $1-\frac{1}{e}-\epsilon$ 的近似解，其时间复杂度为 $O(\epsilon^{-2}k^3n^2m\text{log}n)$

 

改进

（据史学长说）这个贪心算法已经是 $\sigma$ 已知的情况下最好的算法，所以对算法的改进都针对如何更快求 $\sigma$。

首先有一种“剪枝”的方法：假设在当前循环开始之前，种子节点集为 $S$，在之前的某次循环开始之前，种子节点集为 $S'$，显然 $S' \subset S$。如果对于两个节点 $x, y \notin S$，有 $\sigma(S \cup \{x\}) - \sigma(S) \ge \sigma(S' \cup \{y\}) - \sigma(S')$，那么 $y$ 在当前循环中可以不用考虑。因为根据单调子模的性质，$\sigma(S' \cup \{y\}) - \sigma(S') \ge \sigma(S \cup \{y\}) - \sigma(S)$，所以点 $x$ 必然不劣于点 $y$。虽然估计 $\sigma$ 的方法仍然是进行大量模拟实验，在最差情况下复杂度不变，但是这个剪枝据说可以将实际运行效率提高 700 倍。

 另一种改进方法改进的是模拟实验的方式。一个节点 $v$ 被种子节点集 $S$ 激活的概率，等于把所有边反向，然后只激活 $v$，最后 $S$ 里有节点被激活的概率。$v$ 反向激活的节点集被成为 $v$ 的 RR-set (Reverse Reachable Set)。这个事实用数学公式表述如下：$$\mathbb{E}(\sigma(S)) = \frac{n}{\theta}\mathbb{E}(\sum_{i=1}^\theta \mathbb{I}(S \cap \text{RR}(x_i) \ne \emptyset))$$ 其中 $\mathbb{E}$ 表示期望，$\mathbb{I}$ 是指示函数（括号内表达式为真时取 1，为假时取 0），RR 就表示 $x_i$ 的 RR-set。

为了计算等号右边的期望，我们仍然进行模拟实验：循环 $\theta$ 次，每次随机选择一个节点 $x_i$，随机计算它的一个 RR-set（当然，每次随机的结果不同，同一个节点的 RR-set 也会不同），看看 $S$ 中是否有节点位于 RR-set 里，如果有则结果为 1，否则结果为 0。最后取结果的均值乘以总节点数 $n$ 即可。在贪心算法中，我们每次只要选择被最多 RR-set 覆盖的节点加入种子节点集即可。$\theta$ 好像最好是一个 $O(nm)$ 级别的数，但是由于在现实的图中，一个点的 RR-set 不会很大，所以这个方法的效率更高。

我们还可以给 RR-set 这个方法设置一个阈值。只要在随机的过程中，有一个点被超过阈值个 RR-set 覆盖，我们就将它选入种子节点集中。这个阈值的理论值很大，但是在实验中取 16 就能获得较好的效果。比随机 $\theta$ 次的效率更高。