学习理论初步
最近看了 Andrew Ng 机器学习课程的学习理论部分,同时也开始看 The Elements of Statistical Learning,简单整理一下有关学习理论的内容。这篇博客将简单介绍期望泛化损失(expected prediction loss)、经验损失(empirical loss)以及两者之间的关系,还会介绍 bias-variance tradeoff。
期望泛化损失
应该来说,机器学习的最终目的就是要减小期望泛化损失。通过选择不同的损失函数,我们将会推导出不同的预测函数。
假设我们选择经典的平方差(L2-norm)作为损失函数。那么对于一个预测函数 $f(x)$ 来说,它的期望泛化损失可以写为 $$\text{EPE}(f) = \mathbb{E}((Y-f(X))^2)$$ 这个式子可以展开为 $$\text{EPE}(f) = \mathbb{E}_X\mathbb{E}_{Y|X}((Y-f(X))^2)$$ 其中 $\mathbb{E}_X(f(X))$ 表示对 $X$ 的分布求 $f(X)$ 的期望。
我们希望获得的预测函数,应该是在 $X$ 取任意值的情况下,都能将期望损失最小化。所以我们有 $$f(x) = \mathop{\text{argmin}}\limits_{c} \mathbb{E}_{Y|X}((Y-c)^2|X=x)$$ 展开有 $$\mathbb{E}((Y-c)^2) = \mathbb{E}(Y^2)-2c\mathbb{E}(Y)+c^2$$ 这是一个开口朝上的二次函数,在对称轴处取最小值,所以 $$c = \mathbb{E}(Y|X=x)$$ 也就是说,在选择平方差作为损失函数的情况下,最好的预测函数应该输出 $Y$ 的期望。
当然,如果换一个损失函数,答案就有所不同了。例如,我们使用 L1-norm(绝对值)作为损失函数,那么式子变为 $$f(x) = \mathop{\text{argmin}}\limits_{c} \mathbb{E}_{Y|X}(|Y-c|\ |X=x)$$ 这个式子的解是 $$f(x) = \text{median}(Y|X=x)$$ 其中 median 表示中位数。
虽然我不太会证明这个结论,但是我们可以通过这个问题来理解这个结论:一个数轴上有 $n$ 个点,我们要在数轴上选一个位置,使得这个位置到所有点的距离之和最小。$n$ 个点的中位数就是这个问题的解。
经验损失
可是,给出一个训练好的预测函数,我们怎么知道它的期望泛化损失是多少呢?可能有人会说:如果知道所有数据的概率分布,我们就能计算期望泛化损失了。可是机器学习的最终目的就是为了预测数据的概率分布,所以一个模型的期望泛化损失是无从得知的。我们只能通过观察模型在训练样本上的损失(称为经验损失),来推测模型的泛化能力。
一个模型的经验损失小,那么它的泛化损失也小吗?我们首先给出两个引理,帮助我们探究这个问题。
引理 1:设 $A_1, A_2, \dots, A_k$ 为随机事件,那么 $P(A_1 \cup A_2 \cup \dots \cup A_k) \le P(A_1) + P(A_2) + \dots + P(A_k)$;
引理 2:设 $Z_1, Z_2, \dots, Z_m$ 是服从参数为 $\phi$ 的伯努利分布的独立随机变量,令 $\hat{\phi} = (1/m)\sum_{i=1}^mZ_i$,再令 $\gamma > 0$ 为常数。那么 $P(|\phi-\hat{\phi}| > \gamma) \le 2\text{exp}(-2\gamma^2m)$。
引理 1 非常容易证明,考虑一下容斥原理即可;引理 2 就是 Hoeffding inequality,我暂时还不知道怎么证明- -不过 wiki 上有可以看一看...
我们来考虑二分类问题,并使用 0-1 损失函数。那在这个问题中,一个模型 $h$ 的经验损失 $\hat{\epsilon}(h)$ 就可以看作它在训练数据上犯错误的概率,而它的泛化损失 $\epsilon(h)$ 就是在整个数据分布范围内犯错误的概率。也就是说,从数据分布中选取一条数据用 $h$ 进行预测,记随机变量 $Z$ 表示 $h$ 是否预测错误,那么 $Z$ 服从参数为 $\epsilon(h)$ 的伯努利分布。设总共有 $m$ 条训练数据,记 $Z_i$ 表示 $h$ 在第 $i$ 条训练数据上是否预测错误,那么 $\hat{\epsilon}(h) = (1/m)\sum_{i=1}^mZ_i$,我们就可以用引理 2 得到以下式子:$$P(|\epsilon(h)-\hat{\epsilon}(h)| > \gamma) \le 2\text{exp}(-2\gamma^2m)$$ 从这个式子我们可以看出,只要 $m$ 足够大,那么经验损失 $\epsilon(h)$ 和泛化损失 $\hat{\epsilon}(h)$ 就不太可能相差较大。
如果我们现在要从包含 $k$ 个模型的集合 $\mathcal{H}$ 中选取模型,我们当然希望能选到泛化损失最小的模型,但是我们能知道的只有模型的经验损失。那么在一组模型中,泛化损失最小的模型和经验损失最小的模型有什么关系呢?首先,我们由引理 1,可以得到这样一个式子:$$P(\forall h \in \mathcal{H} \quad |\epsilon(h)-\hat{\epsilon}(h)| \le \gamma) \ge 1 - 2k\text{exp}(-2\gamma^2m)$$ 令这个概率至少为 $1-\delta$,我们有 $$1 - 2k\text{exp}(-2\gamma^2m) \ge 1-\delta$$ $$m \ge \frac{1}{2\gamma^2}\text{log}\frac{2k}{\delta}$$ 这个式子表明,只要训练样本超过一定数量,所有模型经验损失和泛化损失之间的差距就会至少以 $1-\delta$ 的概率不超过 $\gamma$。
如果令概率恰为 $1-\delta$,我们有 $$\gamma = \sqrt{\frac{1}{2m}\text{log}\frac{2k}{\delta}}$$ 我们可以用这个式子推导出泛化损失最小的模型 $h^*$ 与经验损失最小的模型 $\hat{h}$ 的泛化能力之间的关系:$$\epsilon(\hat{h}) \le \hat{\epsilon}(\hat{h}) + \gamma \\ \le \hat{\epsilon}(h^*) + \gamma \\ \le \epsilon(h^*) + 2\gamma \\ = \epsilon(h^*) + 2\sqrt{\frac{1}{2m}\text{log}\frac{2k}{\delta}}$$
这个式子从理论上说明了:训练样本越多,经验损失最小的模型的泛化能力就越高...
Bias-Variance Tradeoff
上面这个式子还有另外一个意义,可以用于解释欠拟合(underfitting)和过拟合(overfitting)。考虑一个参数较少、较为简单的模型,虽然它的 $k$ 比较小,降低了第二项的值,但是它的 $\epsilon(h^*)$ 比较大,第一项的值上升了,两者失衡就导致了欠拟合;再考虑一个参数较多、较为复杂的模型,虽然它的 $\epsilon(h^*)$ 比较小,第一项的值下降了,但是它的 $k$ 比较大,第二项的值上升了,两者失衡就导致了过拟合。总体来说,模型复杂度与经验损失和泛化损失的关系如下图:
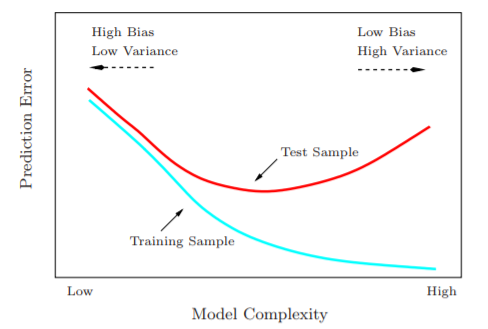
我们希望找到的模型,就是复杂度中等的、泛化损失最低的模型。
当然啦,上面的讨论中我们只描述了模型空间中模型数量有限的情况,对于模型数量无限的情况,式子就和模型空间的 VC dimension 有关。可以简单理解为:模型空间的 VC dimension 越高,模型就越复杂。设模型空间的 VC dimension 为 $d$,那么 $$\epsilon(\hat{h}) \le \epsilon(h^*) + O(\sqrt{\frac{d}{m}\text{log}\frac{m}{d} + \frac{1}{m}\text{log}\frac{1}{\delta}})$$ 据 Andrew 说他读博士的时候为了弄懂这个式子的推导花了一个星期- -
我们也可以从模型泛化损失的表达式中分离出 bias 和 variance。以 K 近邻算法为例,我们使用 L2-norm 作为损失函数。假设数据服从 $Y = f(X) + \epsilon$,其中 $\mathbb{E}(\epsilon) = 0$,$\text{Var}(\epsilon) = \sigma^2$。另外简单起见我们假设所有训练数据的 $X$ 值都已事先确定。用 $\hat{f}_k$ 表示 K 近邻的预测函数,对于一条测试数据 $x_0$,它的期望泛化损失为:$$\text{EPE}(x_0) = \mathbb{E}((y_0-\hat{f}_k(x_0))^2|X) \\ = \mathbb{E}(y_0^2) - 2\mathbb{E}(y_0\hat{f}_k(x_0)) + \mathbb{E}(\hat{f}^2_k(x_0)) \\ = \mathbb{E}(y_0^2) - \mathbb{E}^2(y_0) + \mathbb{E}^2(y_0) - 2\mathbb{E}(y_0\hat{f}_k(x_0)) + \mathbb{E}(\hat{f}^2_k(x_0)) - \mathbb{E}^2(\hat{f}_k(x_0)) + \mathbb{E}^2(\hat{f}_k(x_0)) \\ = \text{Var}(y_0) + \text{Var}(\hat{f}_k(x_0)) + \mathbb{E}^2(y_0) - 2\mathbb{E}(y_0\hat{f}_k(x_0)) + \mathbb{E}^2(\hat{f}_k(x_0))$$ 其中 $\mathbb{E}(y_0) = f(x_0)$,而测试样本与已经用训练样本训练好的模型是无关的,所以 $\mathbb{E}(y_0\hat{f}_k(x_0)) = \mathbb{E}(y_0)\mathbb{E}(\hat{f}_k(x_0))$。那么 $$\text{EPE}(x_0) = \text{Var}(y_0) + \text{Var}(\hat{f}_k(x_0)) + (f(x_0)-\mathbb{E}(\hat{f}_k(x_0)))^2 \\ = \text{Var}(y_0) + \text{Var}(\hat{f}_k(x_0)) + \text{Bias}^2(\hat{f}_k(x_0))$$ 注意到 $\text{Var}(y_0) = \sigma^2$。另外由于 $\hat{f}_k(x_0)$ 是 $k$ 个方差为 $\sigma^2$ 的随机变量的平均数,所以 $\text{Var}(\hat{f}^2_k(x_0)) = \sigma^2/k$。还有 $$\mathbb{E}(\hat{f}_k(x_0)) = \frac{1}{k}\sum_{x \in N_k(x_0)}f(x)$$ 其中 $N_k(x_0)$ 表示 $x_0$ 的 K 近邻。所以式子最终可展开为:$$\text{EPE}(x_0) = \sigma^2 + \frac{\sigma^2}{k} + (f(x_0) - \frac{1}{k}\sum_{x \in N_k(x_0)}f(x))^2$$ 设训练样本有 $m$ 条,我们知道,K 近邻的模型自由度为 $m/k$。这是因为:假如所有邻域都不相交,那么有 $m/k$ 个邻域,而且每个邻域都可以有自己的均值。也就是说,$k$ 越小,模型复杂度越高。
很显然,随着 $k$ 的减小(模型复杂度的提高),期望泛化损失的 variance $\sigma^2/k$ 是在上升的,而如果 $f$ 是一个平滑的函数(在较近的范围内波动不是很大),那么 bias 应该是下降的。通过对期望泛化损失的分解,我们可以形象地看到 bias-variance tradeoff。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号