应用运筹学基础:组合优化 (3) - 近似算法选讲 (1)
这一节课讲解了 vertex cover 的 2 - 近似算法与 unrelated parallel machine scheduling 的 2 - 近似算法。
Vertex Cover
来看一些 vertex cover 的近似算法。
近似算法 1
算法描述:将度数最大的点 $u$ 选入答案集合,并将 $u$ 与端点包含 $u$ 的边都删去。重复这个过程,直到所有边都被删去为止。
这是一个思路非常自然的贪心算法,但是它的近似比非常差。我们来看下面这张图:
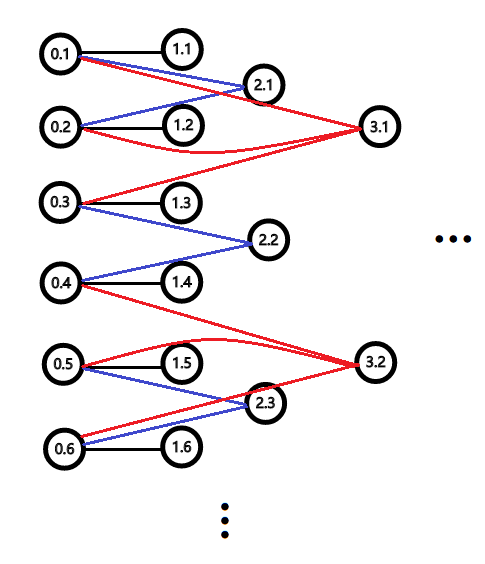
设第一列共有 $n$ 个点,那么这张图一共有 $n + n(1 + \frac{1}{2} + \frac{1}{3} + \dots + \frac{1}{n}) = n + n\ln n$ 个点。
显然,只要将第一列的 $n$ 个点加入答案集合中,就能获得最小的 vertex cover。虽然第一列的 $n$ 个点度数均为 $n$,可是最后一列的点度数也为 $n$。如果我们按照上述的贪心算法选择了最后一列的点,第一列的点度数就会减小至 $n-1$。可是倒数第二列的点度数也为 $n-1$,如果我们选择了倒数第二列的点,那么... 这样下去,我们会把从第二列到最后一列的所有点都选入答案集合,才能获得一个 vertex cover。所以,近似算法 1 的近似比至少为 $\frac{n\ln n}{n} = \ln n$,是一个比较差的算法。
近似算法 2
算法描述:随机选择图中的一条边 $(u, v)$,将 $u$ 与 $v$ 都加入答案集合,并删去 $u$、$v$ 以及所有端点包含 $u$ 或 $v$ 的边。重复这个过程,直到所有边都被删去为止。
这是一个听起来很不自然的算法- -然而该算法的近似比为 2:假设该算法选中了 $k$ 条边,那么这 $k$ 条边是原图中的一个匹配(因为这 $k$ 条边没有相同的端点)。为了覆盖这 $k$ 条边形成的匹配,每条边至少要有一个端点被选中。也就是说,最优解至少为 $k/2$,那么近似比为 2。
近似算法 3
近似算法 2 对于无权的 vertex cover 问题近似比为 2,而带权的 vertex cover 问题需要使用下面这个算法。
设共有 $n$ 个点。用 $x_i$ 表示第 $i$ 个点是否在答案集合中,$w_i$ 表示第 $i$ 个点的权重。用 $E$ 表示边集,$(u, v)$ 表示连接点 $u$ 与点 $v$ 的一条边。写出 vertex cover 要优化的模型。$$\begin{matrix} \min\limits_x & \sum\limits_{i=1}^n w_ix_i \\ \text{s.t.} & x_i + x_j \ge 1 & \forall (i, j) \in E \\ & x \in \{0, 1\} \end{matrix}$$ 这是一个整数规划问题,设该问题的最优目标函数值为 $\text{OPT}$。
对该问题进行 LP 松弛,将 $x \in \{0, 1\}$ 改为 $x \ge 0$。设松弛后的线性规划问题最优解为 $x^*$,最优目标函数值为 $\text{OPT}_{LP}$,显然有 $\text{OPT}_{LP} \le \text{OPT}$。
我们构造原问题的可行解 $x$ 如下:$$x_i = \begin{cases} 1 & x^*_i \ge 0.5 \\ 0 & x^*_i < 0.5 \end{cases}$$ 由于对于每条边 $(i, j)$ 存在 $x^*_i + x^*_j \ge 1$ 的限制,则 $\max(x^*_i, x^*_j) \ge 0.5$,所以 $x_i + x_j \ge 1$ 仍然成立。我们构造的解是可行的。
容易看出,$x_i \le 2x^*_i$。将我们构造的解代入目标函数,有 $$\sum\limits_{i=1}^n w_ix_i \le 2\sum\limits_{i=1}^n w_ix^*_i \\ \le 2\text{OPT}_{LP} \le 2\text{OPT}$$ 这就证明了算法的近似比为 2。
这种“四舍五入”的构造方法在两个东西加起来至少为 1 的限制下似乎挺好用的,可以证明很多近似算法的近似比为 2。
Unrelated Parallel Machine Scheduling
UPMS 问题是说:有 $m$ 台机器和 $n$ 件物品,每件物品都要在一台机器上加工,第 $i$ 台机器加工第 $j$ 件物品的时间为 $a_{i, j}$。求一种把物品分配给机器的方案,使得加工总时长最长的机器,加工总时长最短。
我们很容易写出该问题的优化模型:$$\begin{matrix} \min\limits_{x, t} & t \\ \text{s.t.} & \sum\limits_{i=1}^m x_{i, j} = 1 & \forall j \in \{1, 2, \dots, n\} \\ & \sum\limits_{j=1}^n a_{i, j}x_{i, j} \le t & \forall i \in \{1, 2, \dots, m\} \\ & x_{i, j} \in \{0, 1\} \end{matrix}$$
对这个模型进行 LP 松弛不是一个好主意。假设只有一件物品需要加工,而且该物品在所有机器上的加工时间都为 1。那么原问题的最优目标函数值显然为 1,然而 LP 松弛后的最优目标函数值为 $1/m$(LP 松弛求出的最优解为 $x_{i, 1} = 1/m$),下界太松了,很难进行近似比分析。
但是聪明的数学家们对优化模型进行了一个改动:先二分 $t$ 的值,如果 $a_{i, j} > t$,那么加上 $x_{i, j} = 0$ 的限制(或者直接把这个变量从 LP 中拿走)。很显然,让改动后的 LP 问题存在可行解的最小的 $t$,就是原问题最优目标函数值的下界(用两阶段法的第一阶段判断是否存在可行解即可)。
现在我们通过二分找到了这个最小的 $t$,设改动后的 LP 问题最优解为 $x^*$。对于第 $j$ 件物品,若 $\exists i, x^*_{i, j} = 1$ 那么称该物品为“整数物品”,设共有 $n_1$ 个“整数物品”;否则称该物品为“分数物品”,设共有 $n_2$ 个“分数物品”。显然有 $n_1 + n_2 = n$
容易发现,若第 $j$ 件物品为“分数物品”,那么 $x_{i, j}$ 中至少有两个非零值。由于原问题有 $n+m$ 条限制,根据单纯形法,非零的变量至多有 $n+m$ 个,那么 $n_1 + 2n_2 \le n + m$,得到 $n_2 \le m$。
下面我们给每台机器分配物品,使得每台机器的加工总时长都不超过 $2t$,以此设计一个近似比为 2 的算法。
先进行两个定义:若连通图中边数小等于点数,那么称该连通图为伪树;若一张图的所有连通块都是伪树,那么称该图为伪森林。
构造一张二分图:左边有 $m$ 个点,每个点表示一台机器;右边有 $n$ 个点,每个点表示一件物品。若 $x_{i, j} > 0$ 则连接第 $i$ 台机器和第 $j$ 件物品。如果这个二分图不连通,那么对每个连通块分别求解,最后把解合并起来就是答案,所以我们假设该二分图连通。由于非零变量至多有 $n+m$ 个,所以该连通图的边数不超过点数,是一个伪树。
首先考虑“整数物品”。很显然,每个“整数物品” $j$ 都只和一台机器 $i$ 有连边 $(i, j)$,那就把“整数物品” $j$ 放在机器 $i$ 中加工,并去掉物品 $j$ 和边 $(i, j)$。由于每次恰好去除一个点和一条边,这张图仍然是伪树。显然,此时每台机器的加工总时长至多为 $t$(不然 LP 的最优目标函数值就不只有 $t$ 了)。
这样,图中就只剩机器和“分数物品”了。我们来考虑所有度数为 1 的机器 $i$。假设唯一连接机器 $i$ 的边是 $(i, j)$,那么我们把“分数物品” $j$ 放在机器 $i$ 中加工,并去掉机器 $i$、物品 $j$ 和物品 $j$ 的所有连边。由于每件“分数物品”都有至少两条连边(度数至少为 2),所以我们每次都会去掉两个点以及至少两条边,容易说明剩下的图是伪森林。
反复考虑度数为 1 的机器并进行删除操作,直到最后不存在度数为 1 的机器为止。由于剩下的图是伪森林也是二分图,那么剩下的图中只能包含若干偶环。在偶环上随便给每台机器分配一件物品即可。
这样,每台机器至多分配到一个“分数物品”(别忘了一件物品的加工时间至多为 $t$),再加上原来分配给它的“整数物品”,每台机器的总加工时长至多为 $2t$,这就是一个近似比为 2 的算法。
参考资料
[1] UPMS 的 2 - 近似算法:https://courses.engr.illinois.edu/cs598csc/sp2011/Lectures/lectures_10-11.pdf,第 1 页到第 4 页说得非常明白,应该比我说得要更好...



 浙公网安备 33010602011771号
浙公网安备 33010602011771号