应用运筹学基础:组合优化 (1) - 线性整数规划、割平面法与分枝定界法
这一节课开始了整数规划,并讲解了 Gomory 割平面法与分枝定界法(branch and bound)。
线性整数规划
先从最简单的线性整数规划开始。线性整数规划其实就是线性规划加上解必须为整数的限制,其基本形式为 $$\begin{matrix} \max\limits_x & c^Tx \\ \text{s.t.} & Ax \le b \\ & x \in \mathbb{N} \end{matrix}$$ 我们之前见过的很多算法问题都能写成线性整数规划的形式,特别是能写成整数规划的一种特殊形式:0-1 规划。
0-1 背包问题
设共有 $n$ 件物品,$v_i$ 表示第 $i$ 件物品的价值,$w_i$ 表示第 $i$ 件物品的重量,$c$ 表示背包的最大承重,$x_i \in \{0, 1\}$ 表示是否选择第 $i$ 件物品。那么 0-1 背包问题可以写为 $$\begin{matrix} \max\limits_x & \sum\limits_{i=1}^n v_ix_i \\ \text{s.t.} & \sum\limits_{i=1}^n w_ix_i \le c \\ & x_i \in \{0, 1\} \end{matrix}$$
最小生成树
设共有 $n$ 个点,点集为 $V$,$(i, j) \in E$ 表示从第 $i$ 个点连到第 $j$ 个点的一条有向边(一条无向边就相当于两条有向边),$w_{i, j}$ 表示边权,$x_{i, j} \in \{0, 1\}$ 表示这一条边是否在最小生成树内。那么最小生成树问题可以写为 $$\begin{matrix} \min\limits_x & \sum\limits_{(i, j) \in E} w_{i, j}x_{i, j} \\ \text{s.t.} & \sum\limits_{(i, j) \in E} x_{i, j} = n-1 \\ & \sum\limits_{i \in S, j \not\in S} x_{i, j} \ge 1 & \forall S \;\unicode{x2acb}\; V \\ & x_{i, j} \in \{0, 1\} \end{matrix}$$ 第一项限制保证了生成树中有且仅有 $n-1$ 条边,第二项限制保证了生成树的连通性。因为树是无向图,所以每条边都会被算两次,最后答案除以 2 即可。
虽然这个表述使用了指数级的限制,但我们知道,最小生成树是有多项式算法的。也可以用椭球法在多项式时间内解最小生成树问题。
装箱问题
设共有 $n$ 个物品,$w_i$ 表示第 $i$ 个物品的重量,$c$ 表示每个箱子的承重,$x_{i, j} \in \{0, 1\}$ 表示是否将第 $i$ 个物品放入第 $j$ 个箱子,$y_i$ 表示是否使用第 $i$ 个箱子。那么装箱问题可以写为 $$\begin{matrix} \min\limits_{x, y} & \sum\limits_{i=1}^n y_i \\ \text{s.t.} & \sum\limits_{i=1}^n w_ix_{i, j} \le cy_j & \forall j \in \{1, 2, \dots, n\} \\ & \sum\limits_{j=1}^n x_{i, j} = 1 & \forall i \in \{1, 2, \dots, n\} \\ & x_{i, j} \in \{0, 1\} \\ & y_{i, j} \in \{0, 1\} \end{matrix}$$ 第一项限制保证了每个箱子装的物品不会超过承重,第二项限制保证了每个物品一定会被装入箱子,且每个物品只装入一个箱子。
匹配问题
设图的点集为 $V$,边集为 $E$。设 $(i, j) \in E$ 表示从第 $i$ 个点连到第 $j$ 个点的一条有向边,$x_{i, j}$ 表示这条边是否为匹配边。那么一般无向图的最大匹配问题可以写为 $$\begin{matrix} \max\limits_x & \sum\limits_{(i, j) \in E} x_{i, j} \\ \text{s.t.} & \sum\limits_{(i, j) \in E} x_{i, j} \le 1 & \forall i \in V \\ & \sum\limits_{(i, j) \in E} x_{i, j} \le 1 & \forall j \in V \\ & x_{i, j} \in \{0, 1\} \end{matrix}$$ 我们也可以用图的点 - 边关联矩阵来描述匹配问题。设图中有 $n$ 个顶点,$m$ 条边,那么图的点 - 边关联矩阵是一个 $n \times m$ 的矩阵。该矩阵每列对应一条边,每行对应一个顶点。若第 $i$ 个顶点是第 $j$ 条边的端点,那么矩阵第 $i$ 行第 $j$ 列为 1,否则为 0(可以看出,这个矩阵描绘的是无向边)。
用图的点 - 边关联矩阵将一般无向图的最大匹配问题写为 $$\begin{matrix} \max\limits_{(i, j) \in E} & x_{i, j} \\ \text{s.t.} & Ax \le b \\ & x_{i, j} \in \{0, 1\} \end{matrix}$$ 其中 $A$ 为图的点 - 边关联矩阵,$y$ 是一个全为 1 的向量。
匹配问题中,二分图的最大匹配最为特殊。如果把 $x_{i, j} \in \{0, 1\}$ 这项条件改成 $x \ge 0$,用线性规划求解二分图的最大匹配问题,最优解仍然非 0 即 1。和上一节课讲解的最短路问题一样,这也是因为二分图的点 - 边关联矩阵是全幺模矩阵。
以下对方阵的边长 $n$ 使用数学归纳法,证明任意一个无向二分图的点 - 边关联矩阵的子方阵行列式取值为 0,1 或 -1。
起始步骤:对于任意二分图 $n = 1$ 的子方阵,根据点 - 边关联矩阵的定义,子方阵的行列式取值为 0 或 1。
推递步骤:假设对于任意二分图 $n \le k$ 的子方阵,都有行列式取值为 0,1 或 -1。
对于任意二分图 $n = k + 1$ 的子方阵,根据点 - 边关联矩阵的定义,每一列至多有两个非 0 元素,且这些元素均为 1。
如果该子方阵存在一列没有非 0 元素,那么该子方阵的行列式取值为 0;
如果该子方阵存在一列只有一个非 0 元素,由于该元素为 1,那么该子方阵行列式的绝对值等于该元素余子式的绝对值。将原二分图去掉该元素对应的点和边后,这个余子阵可以看作是新二分图的子方阵(因为二分图的子图仍然是二分图)。根据归纳法假设,该元素余子式的绝对值为 0 或 1,那么该子方阵的行列式取值为 0,1 或 -1。
如果该子方阵的每一列都有两个非 0 元素,设二分图可以被分为 $A$ 和 $B$ 两个集合,根据点 - 边关联矩阵的定义与二分图的定义,将集合 $A$ 中的点对应的行相加,再减去集合 $B$ 中的点对应的行,将会得到一个元素都是 0 的行向量,所以该子方阵的行列式取值为 0。
综上所述,对于 $n = k + 1$ 的子方阵,其行列式的取值仍为 0,1 或 -1。
根据上述数学归纳法,无向二分图的点 - 边关联矩阵是全幺模矩阵。
将二分图的最大匹配问题放松成线性规划后,写出它的对偶问题 $$\begin{matrix} \min\limits_y & \sum\limits_{i=1}^n y_i \\ \text{s.t.} & y_i + y_j \ge 1 & (i, j) \in E \\ & y \ge 0 \end{matrix}$$ 由于全幺模矩阵的转置也是全幺模矩阵,所以这个问题也可以加上 $y \in \{0, 1\}$ 的限制而答案不变。
如果我们把 $y_i$ 看作是否选择第 $i$ 个点,这就是二分图的最小覆盖问题。这就是二分图的最大匹配和最小覆盖可以互相转化的原因。而一般图的最大匹配问题将 0-1 限制放松后最优解会改变,所以无法这样转化。
Gomory 割平面法
接下来介绍两种解线性整数规划问题的方法,首先介绍 Gomory 割平面法。
Gomory 割平面法的思想就是一直去除非整数的最优解,直到某一次求得的最优解为整数。考虑一个线性规划问题,假设我们使用单纯形表求解后获得的不是整数解,我们选择一个非整数的变量 $x_i$,根据单纯形表有 $$x_i + \sum\limits_{j=m+1}^n \bar{a_{i,j}}x_j = \bar{b_i} \qquad \qquad \text{①} $$ 既然 $x_i$ 不是整数,说明 $\bar{b_i}$ 一定不是整数,当然 $\bar{a_{i,j}}$ 也可能不是整数。
将式 ① 调整一下,变为 $$x_i + \sum\limits_{j=m+1}^n \left\lfloor \bar{a_{i,j}} \right\rfloor x_j \le \bar{b_i} \qquad \qquad \text{②} $$ 显然,式 ① 的解一定是式 ② 的解。
再次调整式 ②,变为 $$x_i + \sum\limits_{j=m+1}^n \left\lfloor \bar{a_{i,j}} \right\rfloor x_j \le \left\lfloor\bar{b_i}\right\rfloor \qquad \qquad \text{③}$$ 容易看出,式 ② 的整数解一定符合式 ③,而原来用单纯形表求出的非整数解就不符合式 ③ 了(因为原来求出的非整数解中,有 $x_i = \bar{b_i} > \left\lfloor \bar{b_i } \right\rfloor$ 以及 $x_j = 0$)。我们只要把式 ③ 加入原来的线性规划问题,重新求解多出一个限制的线性规划问题。如果求出来的是整数解就停止,否则继续加入限制并求解,直到获得整数解为止。
顺便一提,大部分参考资料不会直接加入式 ③,而是加入 ① - ③,即 $$\sum\limits_{j=m+1}^n(\bar{a_{i,j}} - \left\lfloor \bar{a_{i,j}} \right\rfloor) x_j \ge \bar{b_i} - \left\lfloor \bar{b_i} \right\rfloor$$ 当然效果是一样的。
来举个例子,考虑以下线性整数规划问题 $$\begin{matrix} \max\limits_x & 3x_1 + 2x_2 \\ \text{s.t.} & 2x_1 + 3x_2 + x_3 = 14 \\ & 2x_1 + x_2 + x_4 = 9 \\ & x \ge 0 \end{matrix}$$ 用单纯形表解该问题,结果为 $$\begin{array}{c|cccc|c} & 0 & 0 & -1/4 & -5/4 & -59/4 \\ \hline x_2 & 0 & 1 & 1/2 & -1/2 & 5/2 \\ x_1 & 1 & 0 & -1/4 & 3/4 & 13/4 \end{array}$$ 选择 $x_2$,加入限制:$x_2 - x_4 \le 2$,即 $x_2 - x_4 + x_5 = 2$。用单纯形表求解加入限制后的问题,结果为 $$\begin{array}{c|ccccc|c} & 0 & 0 & 0 & -1 & -1/2 & -29/2 \\ \hline x_3 & 0 & 0 & 1 & 1 & -2 & 1 \\ x_1 & 1 & 0 & 0 & 1 & -1/2 & 7/2 \\ x_2 & 0 & 1 & 0 & -1 & 1 & 2 \end{array}$$ 选择 $x_1$,加入限制:$x_1 + x_4 - x_5 \le 3$,即 $x_1 + x_4 - x_5 + x_6 = 3$. 用单纯形表求解加入限制后的问题,结果为 $$\begin{array}{c|cccccc|c} & 0 & 0 & 0 & -1 & 0 & -1 & -14 \\ \hline x_3 & 0 & 0 & 1 & 1 & 0 & -4 & 3 \\ x_1 & 1 & 0 & 0 & 1 & 0 & -1 & 4 \\ x_5 & 0 & 0 & 0 & 0 & 1 & -2 & 1 \\ x_2 & 0 & 1 & 0 & -1 & 0 & 2 & 1 \end{array}$$ 所以原问题的最优解为 $x_1 = 4, x_2 = 1$,目标函数值为 $14$。
分枝定界法
(其实我觉得应该写作分支定界法,不过上课的老师坚持认为是分枝- -)
分枝定界法的思想和最优性剪枝或者 min-max 搜索树什么的差不多。我们先将原问题放松成线性规划问题,解这个线性规划,就得到了整数规划最优解的上界。假设最优解中 $N < x_i < N+1$ 不是整数,就会有两种可能:$x_i \le N$ 或 $x_i \ge N+1$,对两种情况分别进行搜索。如果在某一枝内算出了一个整数解,我们就得到了原整数规划最优解的下界;如果另一枝内线性规划问题的解还没有这个下界来得优,那么那一枝就可以直接不考虑了(因为线性规划问题的解是那一枝能找到的最优解的上界)。总而言之就是带着最优性剪枝的暴搜。
用一张 youtube 视频里的图作为例子
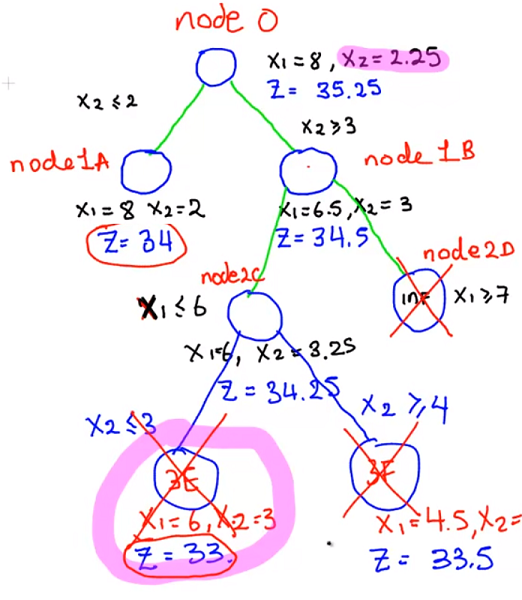
对于放松后的线性规划问题,最优解为 $x_1 = 8, x_2 = 2.25$,目标函数值为 35.25;
首先考虑 $x_2 \le 2$,也就是 node1A,算得该情况下最优解为 $x_1 = 8, x_2 = 2$,目标函数值为 34。这是一个整数解,记录并回溯;
考虑 $x_2 \ge 3$,也就是 node1B,算得该情况下的最优解为 $x_1 = 6.5, x_2 = 3$,目标函数值为 34.5。它还优于我们已知的下界 34,继续搜索;
考虑 $x_1 \le 6$,也就是 node2C,算得该情况下的最优解为 $x_1 = 6, x_2 = 3.25$,目标函数值为 34.25。它还优于我们已知的下界 34,继续搜索;
考虑 $x_2 \le 3$,也就是 node3E,算得该情况下的最优解为 $x_1 = 6, x_2 = 3$,目标函数值为 33。它劣于我们已知的下界 34,回溯;
考虑 $x_2 \ge 4$,也就是 node3F,算得该情况下的目标函数值为 33.5。它劣于我们已知的下界 34,回溯;
考虑 $x_1 \ge 7$,也就是 node2D,该情况下无可行解,回溯;
搜索得最优解为 $x_1 = 8, x_2 = 2$,目标函数值为 34。
(事实上我觉得这个例子不太好,其实在 node1B就可以直接回溯了。因为 node1B 那一枝的上界是 34.5,那么最优整数解最多只有 34 了。)
再试一试 Gomory 单纯形法的那个例子。将原问题松弛为线性规划问题后,得到的最优解为 $x_2 = 5/2, x_1 = 13/4$,目标函数值为 $59/4$。
先探索 $x_2 \le 2$ 的情况,用单纯形表求解得 $$\begin{array}{c|ccccc|c} & 0 & 0 & 0 & -1 & -1/2 & -29/2 \\ \hline x_3 & 0 & 0 & 1 & 1 & -2 & 1 \\ x_1 & 1 & 0 & 0 & 1 & -1/2 & 7/2 \\ x_2 & 0 & 1 & 0 & -1 & 1 & 2 \end{array}$$ 探索 $x_1 \le 3$ 的情况,用单纯形表求解得 $$\begin{array}{c|cccccc|c} & 0 & 0 & 0 & 0 & -2 & -3 & -13 \\ \hline x_3 & 0 & 0 & 1 & 0 & 0 & -2 & 2 \\ x_4 & 0 & 0 & 0 & 1 & 0 & -2 & 1 \\ x_2 & 0 & 1 & 0 & 0 & 1 & 0 & 2 \\ x_1 & 1 & 0 & 0 & 0 & 0 & 1 & 3 \end{array}$$ 得到候选的解 $x_1 = 3, x_2 = 2$,目标函数值为 $13$。
接下来探索 $x_1 \ge 4$,用单纯形表解得 $$\begin{array}{c|ccccc|c} & 0 & 0 & 0 & -2 & -1 & -14 \\ \hline x_1 & 1 & 0 & 0 & 0 & -1 & 4 \\ x_3 & 0 & 0 & 1 & -2 & -4 & 3 \\ x_2 & 0 & 1 & 0 & 1 & 2 & 1 \\ x_5 & 0 & 0 & 0 & 0 & 1 & 1 \end{array}$$ 得到候选的解 $x_1 = 4, x_2 = 1$,目标函数值为 $14$。
注意到原问题目标函数值的上界为 $59/4$,而 $14 < 59/4 < 15$,所以目标函数值的整数上界为 $14$,$x_1 = 4, x_2 = 1$ 必然为整数最优解. 所以原问题的最优解为 $x_1 = 4, x_2 = 1$,目标函数值为 $14$。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号