应用运筹学基础：线性规划 (5) - 原始对偶方法

这一节课讲解了线性规划中的原始对偶方法（primal-dual method），并以最短路问题为例说明该方法的应用。

 

原始对偶方法

原始对偶方法利用的就是上一节课中讲到的互补松弛定理。我们首先找到对偶问题的一个可行解 $y$，并尝试找到一个原问题的可行解 $x$，使得 $x$ 和 $y$ 满足互补松弛定理。如果我们找到了这样的 $x$，那么 $x$ 和 $y$ 就分别是原问题和对偶问题的最优解；否则我们就需要调整 $y$，让它变得更好，继续尝试，直到找到最优解为止。

寻找对偶可行解

考虑以下线性规划问题作为原问题 $$\begin{matrix} \min\limits_x & c^Tx \\ \text{s.t.} & Ax = b \ge 0 \\ & x \ge 0 \end{matrix}$$ 它的对偶问题为 $$\begin{matrix} \max\limits_x & b^Ty \\ \text{s.t.} & A^Ty \le c \end{matrix}$$ 我们首先需要获得一个对偶问题的可行解。如果 $c \ge 0$，显然 $y = 0$ 就是对偶问题的一个可行解，否则我们可以使用如下方法寻找可行解。

给原问题增加一个变量与一条约束 $x_1 + x_2 + \dots + x_n + x_{n+1} = b_{m+1}$，其中 $b_{m+1}$ 需要足够大，至少要大等于 $x_1 + x_2 + \dots + x_n$ 可能的最大值。这样的约束就不会改变原问题。

加入新约束后，我们写出新的对偶问题 $$\begin{matrix} \max\limits_y & b^Ty + b_{m+1}y_{m+1} \\ \text{s.t.} & A^Ty + y_{m+1}\begin{bmatrix} 1 & 1 & \dots & 1 \end{bmatrix}^T \le c \\ & y_{m+1} \le 0 \end{matrix}$$ 我们很容易看出这个新对偶问题的可行解为 $y_i = 0 \quad \forall i \in \{1, 2, \dots, m\}$ 以及 $y_{m+1} = \min\limits_i \quad c_i$。

限制的原问题 (RP) 与限制的对偶问题 (DRP)

假设我们找到了对偶问题的可行解 $y$，现在我们需要寻找一个原问题的可行解 $x$ 满足互补松弛定理。

设 $A_j$ 表示矩阵 $A$ 的第 $j$ 列，定义 $J = \{ j | A_j^Ty = c_j \}$（称 $J$ 为允许指标集，简单来说 $J$ 就是以 $y$ 作为对偶可行解时，对偶问题中较紧的那些限制的编号）。根据原问题的定义和互补松弛定理，我们有 $$Ax = b \\ x_j = 0 \quad \forall j \not\in J \\ x_j \ge 0 \quad \forall j \in J$$ 如果我们能找到一个 $x$ 满足上面三个条件，$x$ 和 $y$ 就能满足互补松弛定理。

为了获得一个可行的 $x$，我们使用一个类似于两阶段法的思想（虽然两阶段法和原始对偶方法可能没啥联系- -），构造一个优化问题，称为限制的原问题（restricted primal，RP）$$\begin{matrix} \max\limits_x & \sum\limits_{i=1}^m \bar{x}_i \\ \text{s.t.} & \sum\limits_{j\in J} a_{i,j}x_j + \bar{x}_i = b_i \\ & x_j \ge 0, \bar{x}_i \ge 0 \end{matrix}$$ 很显然，若目标函数值取 0，那么我们就找到了满足互补松弛定理的 $x$。

我们再来写出 RP 的对偶问题，称为限制的对偶问题（DRP）$$\begin{matrix} \max\limits_x & b^Ty \\ \text{s.t.} & A^T_jy \le 0 & \forall j \in J \\ & y_i \le 1 & \forall i \in \{1, 2, \dots, m\} \end{matrix}$$ 设 $\bar{y}$ 为 DRP 的最优解，根据强对偶定理，若 $b^T\bar{y} = 0$ 则 RP 的目标函数值也可以取到 0，那么当前对偶可行的 $y$ 就是对偶问题的最优解；否则我们有 $b^T\bar{y} \ge 0$，因为至少 $\bar{y} = 0$ 是 DRP 的可行解。

一开始要求原问题的 $b \ge 0$ 可能是为了保证 RP 问题有可行解（如果 $b \ge 0$ 那么 RP 问题至少有可行解 $x = 0$ 和 $\bar{x} = b$）。不过这可能也不是很有必要，如果发现 RP 问题无可行解，或者 DRP 问题无有限最优解，那就说明了原问题无可行解。

改进当前的对偶可行解

如果 DRP 的最优解让 DRP 的目标函数值超过 0，说明当前的 $y$ 还不是最优的。我们来想办法用 $\bar{y}$ 改进 $y$。我们让新的对偶可行解 $\hat{y} = y + \theta\bar{y}$（其中 $\theta \ge 0$），显然有 $b^T\hat{y} = b^Ty + \theta b^T\bar{y} > b^Ty$，说明对偶问题的目标函数值的确改进了。但别忘了，$\hat{y}$ 仍然需要是对偶可行的，也就是说，$A^T\hat{y} = A^Ty + \theta A^T\hat{y} \le c$ 仍要满足。

我们来考虑 $\theta$ 的取值范围。对于 $j \in J$，因为 $A^T_j\bar{y} \le 0$，无论 $\theta$ 取多大，都不会超过 $c$ 的限制，所以这些项不会限制 $\theta$ 的取值；对于 $j \not\in J$，我们选择 $$\theta = \min_{j \not\in J, A^T_j\bar{y} > 0} \quad \frac{c_j - A^T_jy}{A^T_j\bar{y}}$$ 这样就会让 $j \not\in J$ 中的一条限制变紧，其它限制则不会超过，仍然是对偶可行的。当然啦，如果 $\theta$ 可以无限增大，说明对偶问题没有有限最优解，那么原问题无可行解。

将 $y$ 调整为 $\hat{y}$ 之后，就进入下一轮迭代继续调整（当然我们不需要再从原问题开始，慢慢写出 RP 和 DRP 了，直接确定新的 $J$ 和新的 DRP 即可），直到 DRP 的最优解让目标函数值为 0，此时的 $y$ 就是对偶问题的最优解。

算法的时间复杂度

事实上，原始对偶问题就是通过枚举 $J$ 来获得对偶问题的最优解。由于 $J$ 至多有 $2^n$ 个，所以这个方法是一定会终止的。当然，这个方法的最差复杂度也是指数级的。如果限制条件在进入 $J$ 后不会出来，那么算法就能在线性步数内结束。

这个方法看起来比单纯形法麻烦多了。单纯形法只要解一个优化问题就能得到最优解，这个方法一下子变出来四个优化问题。但是这个方法对特定问题是非常有效的，对于一些特定问题来说，我们可以一下子看出（或者在很短的时间内方便地算出）DRP 的最优解。下面就来举例说明原始对偶方法的应用。

 

应用：最短路问题

用线性规划表示最短路问题

我们来考虑有向图上的最短路问题，起点为 $s$，终点为 $t$。对有向图定义点 - 弧关联矩阵，这个矩阵中每列对应一条边，每行对应一个顶点。若一条边是一个顶点的出边，那么矩阵对应元素为 1；若一条边是一个顶点的入边，那么矩阵对应元素为 -1。设 $w_i$ 表示第 $i$ 条边的长度，$x_i$ 表示第 $i$ 条边是否在最短路上，那么最短路问题就是解如下线性规划问题 $$\begin{matrix} \min\limits_x & w^Tx \\ \text{s.t.} & Ax = v \\ & x \ge 0 \end{matrix}$$ 其中 $$v_i = \begin{cases} 1 & i = s \\ -1 & i = t \\ 0 & \text{otherwise} \end{cases}$$ 虽然这个问题是一个线性规划问题，但是最优解中每个变量的值不是 0 就是 1（最短路问题中不会有半条边在最短路上吧- -）。最优解中每个变量的取值范围在 0~1 之间还好理解（如果有一个变量大于 1，就必须有变量取负值，这样不满足 $x \ge 0$ 的条件），为什么每个变量的取值还是整数呢？

我们使用单纯形法求解时，得到的解是 $x_B = A_B^{-1}b$。如果 $A_B^{-1}$ 和 $b$ 的元素都是整数，得到的解自然是整数。我们引入全幺模矩阵（total unimodular matrix）的定义：一个整数矩阵 $A$ 称为全幺模矩阵，如果 $A$ 的任何一个子方阵的行列式取值为 0，1 或 -1。如果我们能证明有向图的点 - 弧关联矩阵是全幺模矩阵，那么 $A_B$ 的行列式取值就为 0，1 或 -1。由于 $A_B^{-1} = A_B^* / |A_B|$，而由于 $A_B$ 的元素均为整数，伴随矩阵 $A_B^*$ 的元素也为整数，那么 $A_B^{-1}$ 的元素自然也都是整数了。

 

以下对方阵的边长 $n$ 使用数学归纳法，证明任意一个有向图的点 - 弧关联矩阵的子方阵行列式取值为 0，1 或 -1。

起始步骤：对于任意有向图 $n = 1$ 的子方阵，根据点 - 弧关联矩阵的定义，子方阵的行列式取值为 0，1 或 -1。

推递步骤：假设对于任意有向图 $n \le k$ 的子方阵，都有行列式取值为 0，1 或 -1。

对于任意有向图 $n = k + 1$ 的子方阵，根据点 - 弧关联矩阵的定义，每一列至多有两个非 0 元素，且这些元素中至多一个为 1，至多一个为 -1。

如果该子方阵存在一列没有非 0 元素，那么该子方阵的行列式取值为 0；

如果该子方阵存在一列只有一个非 0 元素，由于该元素为 1 或 -1，那么该子方阵行列式的绝对值等于该元素余子式的绝对值。将原有向图去掉该元素对应的点和边后，这个余子阵可以看作是新有向图的子方阵. 根据归纳法假设，该元素余子式的绝对值为 0 或 1，那么该子方阵的行列式取值为 0，1 或 -1；

如果该子方阵的每一列都有两个非 0 元素，那么根据点 - 弧关联矩阵的定义，对该子方阵的每一行求和，将会得到一个元素都是 0 的行向量，所以该子方阵的行列式取值为 0。

综上所述，对于 $n = k + 1$ 的子方阵，其行列式的取值仍为 0，1 或 -1。

根据上述数学归纳法，有向图的点 - 弧关联矩阵是全幺模矩阵。

最短路问题的对偶问题和 DRP

根据点 - 弧关联矩阵的定义很容易发现，把 $A$ 的每一行加起来，最后会获得都是 0 的一行，也就是说 $A$ 中的行向量是线性相关的。那么不妨从 $A$ 中去掉代表终点 $t$ 的那一行，得到新矩阵 $\bar{A}$。这样，最短路问题就变为 $$\begin{matrix} \min\limits_x & w^Tx \\ \text{s.t.} & \bar{A}x = v \\ & x \ge 0 \end{matrix}$$ 其中 $$v_i = \begin{cases} 1 & i = s \\ 0 & \text{otherwise} \end{cases}$$ 我们写出这个问题的对偶问题 $$\begin{matrix} \max\limits_{\pi} & \pi_s \\ \text{s.t.} & \pi_i - \pi_j \le w_e & \forall e = (i, j) \in E \\ & \pi_t = 0 \end{matrix}$$ 其中 $(i, j)$ 代表一条从 $i$ 连到 $j$ 的边，$E$ 是有向图的边集。这个对偶问题的可行解很容易得到，只要令$\pi = 0$ 即可。另外，虽然 $\bar{A}$ 矩阵比 $A$ 矩阵少了代表 $t$ 的那一行，但是只要我们定义 $\pi_t = 0$，就又能把对偶问题写成上面的形式了。这个形式就是差分约束系统，以前做算法竞赛的时候一直不能理解为什么差分约束求最大值反而要跑一个最短路，现在终于明白了，原来差分约束是最短路问题的对偶问题...

我们再来写出最短路问题的 DRP $$\begin{matrix} \max\limits_{\pi} & \pi_s \\ \text{s.t.} & \pi_i - \pi_j \le 0 & \forall (i, j) \in J \\ & \pi_i \le 1 \\ & \pi_t = 0 \end{matrix}$$ 这个 DRP 问题的解是非常容易看出的。如果从点 $s$ 到某个点 $p$ 的最短路已经算出来了，而边 $j$ 就在这条最短路上，根据最短路的三角不等式，这条边一定在 $j$ 中。我们把所有已知最短路的点构成的连通块称为 $C$，为了让 $\pi_s$ 的取值最大并满足 DRP 的限制条件，$C$ 中所有点的变量值都必须和 $\pi_s$ 相同。显然，若 $t \not\in C$，那么 $\pi_s = 1$；若 $t \in C$，那么由于 $\pi_t = 0$ 的条件，$\pi_s = 0$，说明我们找到了从 $s$ 到 $t$ 的最短路。

我们用一张有向图来模拟一下最短路的原始对偶算法。

 

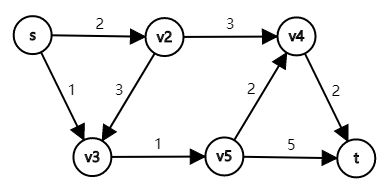
$$\begin{array}{c|cccccc} \text{iter}. & \pi_s & \pi_{v2} & \pi_{v3} & \pi_{v4} & \pi_{v5} & \pi_t \\ \hline 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 & 0 & 0 & 0 \\ 2 & 2 & 0 & 1 & 0 & 0 & 0 \\ 3 & 4 & 2 & 3 & 0 & 2 & 0 \\ 4 & 6 & 5 & 4 & 2 & 4 & 0 \end{array}$$ 其实这就是我们熟悉的 Dijkstra 算法的过程。