导数最终章

思考

以前总是分不清，导数和导函数，
首先明白什么是导数，

• 导数

  • 描述某点的领域的变换

  • \[\lim_{x->x_0}\frac{\Delta y }{\Delta x} =\lim \frac{f(x_0+\Delta x)-f(x_0)}{\Delta x} \]

• 导函数，其实也相当于函数，只是由无数个导数组成的函数

题型

题型1

对应求某点的值，一般就是用定义来做，如果是一段区间，直接用对函数求导法则

这题感觉很奇妙，B连续性质，就是左右极限相等且等于\(f(x_0)\),

D,在某点可导，用定义做，看定义的左右极限存在且相等否，

题型2

题型3

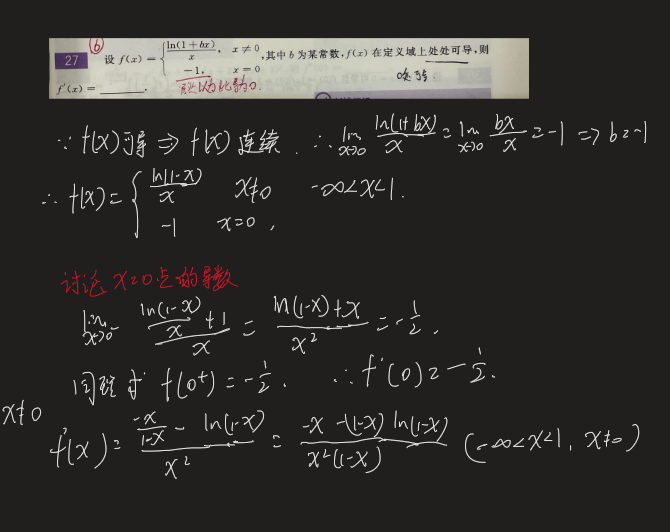
理解

\(\lim_{x->x_0^+}f'(x) =\lim_{x->x_0^-}f'(x) = a\)

这里的是先对导函数求导，在极限，只能判断导函数趋于\(x_0\)的点极限存在，和\(f'(x_0)\)是没有关系的，\(f'(x_0)\)是用定义求出导函数存在性质