夹逼准则和可爱因子

夹逼准则

对于$x_n \leq y_n \leq z_n$,且

$$\lim_{n->\infty} x_n = \lim_{n->\infty} z_n =a$$

则$\lim_{n->\infty} y_n = a$

通俗意义

大概就是我被夹杂在中间，那么我两边的都为a,那么我也必定为a

夹逼实例

对于多种分式相加，方法

• 1，夹逼
• 2，可爱因子

如$\lim_{n->\infty}{\frac{n}{n^2 + 1} + \frac{n}{n^2 + 3} +\frac{n}{n^2 + 2} + ...+\frac{n}{n^2 + n}}$,对于这种式子，首先想到的是夹逼，

• 找通项$\frac{n}{n^2 +i}$
• 令上面的式子为f(x)
• $\frac{n^2}{n^2+n} \leq f(x) \leq \frac{n^2}{n^2+1}$
• $\lim_{n->\infty}\frac{n^2}{n^2 + n} = \lim_{n->\infty}\frac{n^2}{n^2+1} = 1$
• 那么f(x) = 1
• 以后看到这种直接化分母，因为分子化相同了，后面就没办法相加减

可爱因子

$\lim_{n->\infty}(\frac{1}{n+1} + \frac{1}{n+2} +...+\frac{1}{n+n}) =$

$$\int_0^1f(x)dx = \lim_{\lambda->0}\sum_{i=1}^{n}f(\xi_i)\Delta x_i = \lim_{n->\infty}\frac{1}{n}\sum_{i=1}^{n}f(\frac{i}{n})$$

可爱因子大概意思就是，将[0,1]区间分成n分，求图形面积，每段的函数值就是高是变换的$f(\frac{i}{n})$,那么走面积就是求和，也可以直接定积分$\int_0^1f(x)dx$

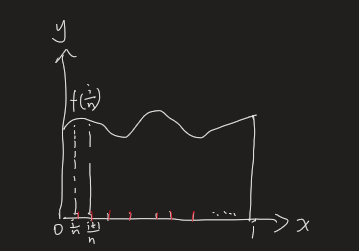
区分积分可爱因子和夹逼

• 式子都是很长的分式相加减
• 首先是同一夹逼做，不行就积分
• 当然其实可爱因子有和很显著的特征就是能提一个$\frac{1}{n}$，且很长的分式的变量范围是从[0,1]，