泰勒

泰勒的来历

前置知识：微分（知道微分是一个近似的估计 \(dy \approx \Delta y\)就差不多微分推导）

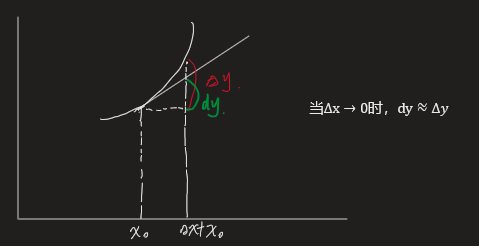
• 推导：
  当|x|很小，那么\(e^x \approx x + 1, \ln (x + 1) \approx x\)，这种精确并不高，主要是由于由o(x)的高阶无穷小，这里有个知识\(\lim_{x->x_0} f(x)= A\),那么当\(x->x_0的时候f(x) = A + o(x)\)，一个道理，那么为了无限接近图像，这里猜想更多的高次来无限逼近函数(所以说泰勒是对函数图像的无限拟合),
  • 下面是对公式的猜想，数学基本上都是靠推理，猜想出来，条件f(x)在\(x_0\)处有n阶导数
  • \(P(x) = a_0 + a_1(x - x_0) + a_2(x - x_0)^2+....+a_n(x - x_0)^n\)(此处全靠猜想)
  • 上面用\(p_n(x)模拟了f(x)\)那么\(f(x) - p_n(x)那么久等于一个(x-x_0)的一个高阶无穷小\),也许会有疑问，为什么\(f(x) - p_n(x)\)还是有差值，不为零，那么即使是双胞胎太也有不同，这只是无限的图像逼近，只是项数越多，图像越接近，但是两者始终不完全相等，因为这是无穷项，这是对于现实生活可能满足条件了
  • 那么又来假设了，假设\(p_n(x)\)在\(x_0\)处的函数值及他的的n阶导数在\(x_0\)处的值依次与\(f(x_0),f'(x_0)...f^{(n)}(x)\)相同，即满足
  • \(p_n(x_0) = f(x_0)\)
  • \(p_n'(x_0) = f'(x_0)\)
  • \(p_n''(x_0) = f''(x_0)\)
  • \(p_{n}^{(n)}(x_0) = f^{(n)}(x)\)
  • 上面公式这是一种粗糙的假设
  • 上面这些式子主要是为了求a
  • 那么\(a_0 = f(x_0), 1* a_1 = f'(x_0), 2!a_2 = f''(x), .... n!a_n = f^{(n)}(x_0)\)这给
  • 求得\(a_0 = f(x_0), a_1 = f'(x_0), a_2=\frac{f''(x_0)}{2!}\),这么求比如2阶导数，那么前面因为小于二阶，最后都为零了，二次后面直接看出无穷小，那么\((x - x_0)^2最后变成2*多少\)
  • 由于\(f(x) 近似p_n(x)\)带入a

  • \[f(x) = f(x_0) + f'(x_0)(x-x_0) + \frac{f''(x_0)}{2!}(x-x_0)^2+...+\frac{f^{(n)}(x_0)}{n!}(x-x_0)^n + R_n(x) \]

  • 推导结束

概念：

泰勒是对函数图像的逼近，无限拟合函数，当泰勒展开式越长那么泰勒公式有越接近函数图像

• 拓展泰勒低阶与高阶
  • 泰勒的低阶项，也就是泰勒公式前面的项，是一种粗糙的图像模拟，
  • 后面高阶项可以直接包含到\(o(x^n)\)中，
  • 具体参考极限与函数的关系 \(\lim_{x->x_0}f(x) = A\) =>当\(x->x->x_0,f(x) = A + o(x)\),这也说明了函数与极限的关系，区间在\(x_0\)的去心领域，只是无限逼近

求极限何时等价代换

在一些书上说的，等价代换一般有条件，说的是只有乘除能等价，后面又拓展了加减部分能直接用等价，讨论何时用等价

等价前提

首先知道为什么一些能等价，一些不能等价，这里面其实就包含了无穷小的思想

加减等价

• 虽热有无穷小，但是无穷下也是有大小的，即在微观的世界，也能区分处大小，就引申处了高阶无穷小，低阶无穷小，等价无穷下，......

• 这里相当于你又1亿1分钱，那么完全可以忽略一分，但是当用了一亿后，那么一份对于自己又显示的很重要，那么加减同理 如果x->0时sinx - x 为什么不直接等于零，按理说当x -> 0 时sinx ~ x所以这里sinx - x就为零，那么答案是否正确？首先我们用泰勒展示

• 推理：x->0时 sinx - x是否为零

  • 泰勒公式得\(x_0 = 0\)
  • \(\sin x= 0 + \frac{cosx_0}{1!}x + o(x) = x\)
  • \(x + o(x)的高阶无穷下类别上面钱的例子，我加上高阶无穷下也没有多大的意义\)
  • 所以x->0时sinx ~ x
  • 那么sinx - x可以用刚才的式子看到，减后就为高阶无穷小，后面分别是
  • \(- \frac{1}{6}x^3 + o(x^3)\),高阶无穷小无意义，那么久近似\(- \frac{1}{6}x^3\)

• 总结：当常用公式在两个多项式式子相减为零的时候，如果其中式子存在泰勒公式，那么这样的等价就存在错误，

乘除等价

我们是书上说乘除能等价x->0

• 还是看sinx*x,sinx泰勒
• sinx = x + o(x),那么当sinx的泰勒展开时，乘以x后面还是x的高阶无穷下，所以没影响
• 又举例：
• \(\sin x * \ln(1+x)\)为什么能直接等价\(x^2\),sinx泰勒展开就不讨论了，这里看\(\ln (1+x)\)
• \(\ln(1+x) = x + o(x)\),结果就是 \((x + o(x)) * (x + o(x))\),式子为
• \(x^2 + 2*x*o(x) + {o(x)}^2\),又泰勒公式可得，\(x*o(x)\)其实应该小于x反正变小了，具体为多少要将泰勒展开，其实是为\(a(x*x^2)\),a是系数，不用关，反正小于x就行,最后还是\(x^2\)
• 那么经历了上面的乘除法，意思就是所有的乘除法等能直接代换？，这里给出的答案是否定的，

乘法等价不是万能换

首先这里说的乘法等价的乘法说的是乘以整个式子，对于局部乘法，一般是不能换的，如AB-C这种式子，假如A能等价，有时候就不能直接等价，看情况（这里可能晕了，一会能等价，一会不能等价，那么什么时候能等价，什么时候不能等价？，其实很简单，不要急）

• 先讨论直接等价
  • 直接等价首先是乘以整个式子如A(B-C),这里A如果能换，就能直接换 \(\frac{B-C}{A}\)这种不在局部乘除，而是乘以整个式子,这种随便换，就相当于AB这种形式，不用记忆，反正逻辑很简单，推一下就行，如：\(\frac {\sin x (x - 1)}{x}\)可写成泰勒\(\frac{(x + o(x)) * (x - 1)}{x}\) = \(\frac{x^2 - x + x*o(x) - o(x)}{x}\),泰勒可得\(o(x) = -\frac{x^3}{6} + o(x^3)+ ...\)那么乘以x还是为零，所以最终\(x - 1\)与直接将sinx ~ x一样
• 那么不能直接等价
  • \(\lim_{x->0}\frac{e^xsinx - x(1 + x)}{x^3}\)
  • 所以这里直接sinx ~ x对否？ 然后就为\(\frac {e^x-(1 + x)}{x^2}\)最后就为0，当你还在沾沾自喜，感觉好简单，但是此时你已经进入了一个圈套局部等价不能化
  • 正确方法，可能这道题难度不太适合举此例
  • 分析：对于这种题，如果用泰勒，那么首先想到的是将分子也写称\(x^3\)形式，和分母抵消，为什么，首先你这样想如果分子小于三次，那么就为无穷，极限都不存在，如果大于三次，其实是o(x^3)所以为什么要三次不用我说了把，大于三次就是三次的高阶无穷小，除以\(x^3\)为零，最后还是算小于等于三次的
  • 读者可能迷惑，分子泰勒展开能无限项，那么展开到那种地步，如前面所说，既然都讲到这了，那么说明下，就这题找\(x^3\)那么就要找所有x的三次，
  • 因为\(e^x\)从一开始，那么相当于sinx就要走到\(x^3\)的三次这种，因为sinx从x开始，那么\(e^x\)就展开到x的二次,即：
  • \(sinx = x - \frac{x^3}{6} + o(x^3)\)
  • \(e^x = 1 + x + \frac{x^2}{2!} + o(x^2)\)
  • 

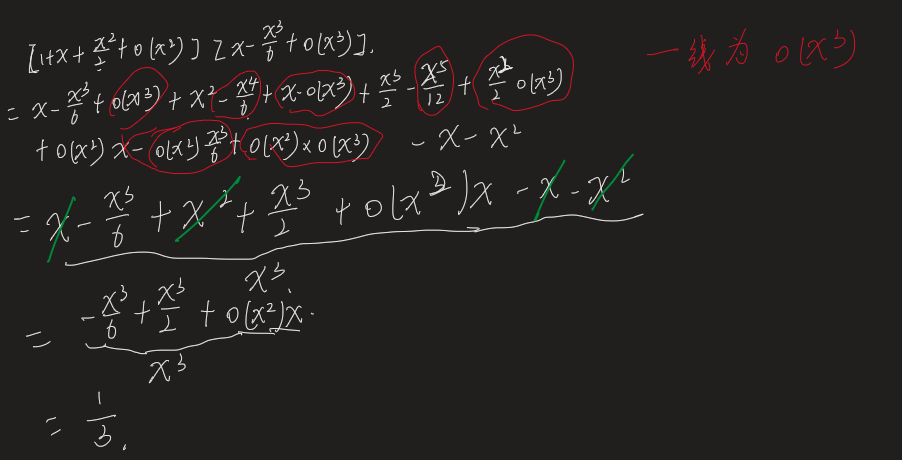
实例：

一般是分式，关于展开到第几项，看分母项数，分母是多少项就展开到多少项，

对于极限做题，一般就泰勒，和洛必达，而用泰勒的情况，一般就是分式，然就是两个变量相减这种情况，

实例一：理解高阶n次和n次

• 题
  

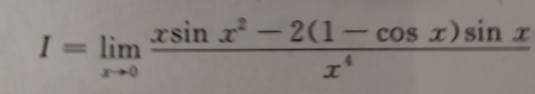
• answer：
  

• 分析
  方法洛必达（麻烦）/泰勒

泰勒
分母是4次，所以要使得分子展开为4次

原式

为什么\(xsinx^2\)中\(- \frac{1}{6} x^7\)省略了写入到\(o(x^4)中了\)

实例二 分式分母未知分子展开：

• 分式：对于不知道分母次数而分子为两个式子相减，\(\frac{A-B}{x^n}\)这种，只需要分母同次幂相减不为零，什么意思，求生你A展开多少项，B展开多少项，比如A的\(ax^n\)次,和B\(bx^n\),如果a-b不为零就停止，后面不要了，如果为零就继续展开，
• 那么问题来了，为什么前面为零就继续展开，有点像《钱的故事》，首先当不为零，后面的都是他的高阶无穷小，也就没必要考虑，那么因为前提条件就是同次相减不为零，那么就表明他前面的没有，后面的太小，那么久只有它，
• 如\(\lim_{x->0}\frac{e^{x^2} - cos{2x}}{ax^b} =1\)
• 泰勒：
  • \(e^x = 1 + x + \frac {x^2}{2!} + o(x^2)\)
  • \(cosx = 1 - \frac {x^2}{2!}+o(x^2)\)
• 这里\(e^{x^2}已经是2次所以只展开两项\)相当于，对于常数如sinx那么就按常规展开，对于\(sin x^2\)要把2次算进去
• 原式 = \(\lim_{x->0} \frac{[1+x^2+o(x^2)] - [1-\frac{4x^2}{2!} + o((2x)^2)]}{ax^b}\)
• = \(\lim_{x->0} \frac{3x^2}{ax^b}\) 因为极限存在
  分子为零，所以b = 2 a = 3

补充

• \(x*o(x)\)其实就是\(o(x^2)\)的无穷下，

  • 证明：
    • \(\frac{x*o(x)}{x^2} = \frac{o(x)}{x} = 0\)

• 总结：就是将\(x^no(x^m) = o(x^{(n+m)})\)

• 对于常数如sinx那么就按常规展开，对于\(sin x^2\)要把2次算进去

参考

泰勒推导参考同济教材(7版本)p138