微分

微分（一元）

这里的微分，是在\(\Delta x - >0\)的情况下 y的变换，近似处理为\(\Delta y \approx dy\)
这里要拓展一个知识点： 极限以无穷下的概念\(\lim_{x->x_0} f(x) = A\) 那么\(f(x_0) = A + o(x)\)为什么会有这样的公式，首先是极限是在一个去心领域（领域就是它附近，无限接近它，但是去心后就不等于它）

那么\(dy = \Delta y+o(x)\) 个人认为o(x)的在左右的无关系，因为本身就是无限靠近零的数字

几何意义：表示函数在切线上都增量

微分的定义

如果函数y = f(x)在\(x_0\)的某一领域有定义，如果函数的增量\(\Delta y = f(x_0 + \Delta x) - f(x_0)\)可以表示

\[\Delta y = A\Delta x + o(\Delta x) \]

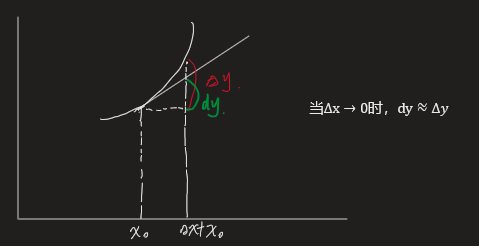
他们之间的关系如上图，可想而知，当\(\Delta x\)无限趋近0时，那么\(\Delta y \approx dy\)

\(dy = f'(x) dx ,其中f(x) = tan \alpha\)

导函原函奇偶性质

1.这里首先给出前置知识：

• 奇函数 X 偶函数为 = 奇函数
• 偶函数 X 偶 = 偶
• 奇函数 X 奇函数 = 偶，
• （总结：奇函数 X 某个函数（有奇偶性质） 性质发生改变）
• 百度百科

证明：奇函数的导数为偶函数

• f(x) = - f(-x);两边同时导数
• f'(x) = f'(-x) * (-1);后面乘以-1是-x的导数

隐函数求导

• 隐函数和多元关系

• 两种方法:

  • 方法1：如y = y(x)函数， \(y^2x + x = 0\) 这种对x求导，\(2yy'x + y^2 + 1 = 0\)，将y做为复合函数
  • 方法2：\(y' = - \frac {F'_x}{F'_y}\) ,将整个式子看为F(x,y),变成多元函数求导，对一个求导，将另一个看出常数
    • \(F(x,y) = y^2x + x\)
    • \(F'_x = y^2 + 1\), \(F'_y = 2yx\)
    • \(y' = - \frac {y^2+1}{2yx}\)

反函数求导

\(y = f(x)\)在某个区间单调可导，且\(f'(x) \neq 0\)其反函数x = \(\varphi(y)\)在对应的区间可导，且

\[\varphi' (y) = \frac {1}{f'(x)} \]

原函数的导数等于反函数导数的倒数

参数方程求导

\(\begin{cases} x = \varphi(t)\\ y = \psi(t)\\ \end{cases}\)
\(\psi\)(t) 与\(\varphi(t)\)都可导
则\(\frac {dy}{dx} = \frac {\psi(t)}{\varphi(t)}\) = \(\frac{dy}{dt} * \frac {dt} {dx}\)

二阶

\(\frac {d^2y}{dx^2} = \frac {d}{dt} (\frac {\psi'(t)}{\phi '(t)})*\frac{1}{\varphi(t)}\)

可导可微，连续的关系

可导可微

可导连续