函数连续推出原函数可导
- 说实话,感觉这个很好笑,我既然都有导函数,那么原函数在区间各点还不可以导么
- 正经推:
设f(x)在区间[a,b]连续,那么原函数可表示(积分上限函数)∫xαf(x)dx,且知道该积分在 x∈[a,b]
时一定存在。
= limh−>0F(x+Δx)−F(x)h
= limh−>0∫x+hαf(x)dx−∫xαf(x)dxh
=limh−>0∫x+hαf(x)dx+∫αxf(x)dxh
=limh−>0∫x+hxf(x)dxh (积分中值定理,此定理有时根据牛顿-莱布尼兹)
=limh−>0f(ξ)∫x+hxdxh (x < ξ < x+h)
=limh−>0f(ξ)hh ()
=limh−>0f(ξ) (f(x)连续 h->0 上面x<ξ<x+h 推出 h->x)
= f(x)

其中微分中值定理
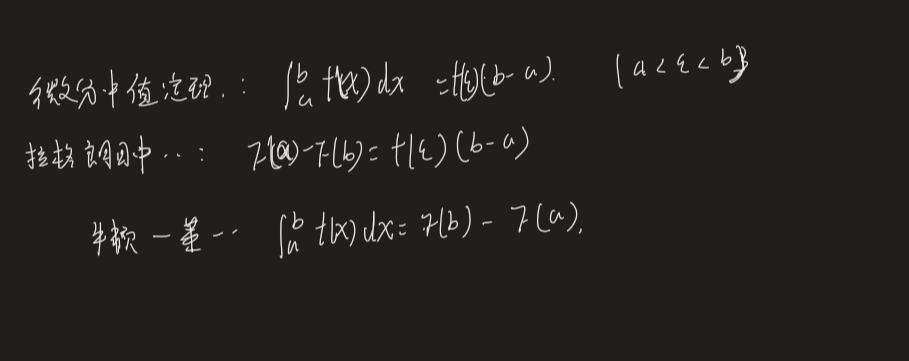
积分上限导数为原函数
首先前置知识:定积分的导数:
(∫q(x)p(x)f(x)dx)′=f(q(x))∗q′(x)−f(p(x))∗p′(x)
那么积分上限函数∫xaf(x)dx 原函数应该是F(x)
牛顿-莱布尼兹推积分中值定理
∫baf(x)dx=F(x)|ba=F(b)−F(a) 拉格朗日中值(这里又要推导连续可导性质了)
原式 = F(ξ)(b−a)=F(ξ)∫badx
还有个
参考
半个冯博士

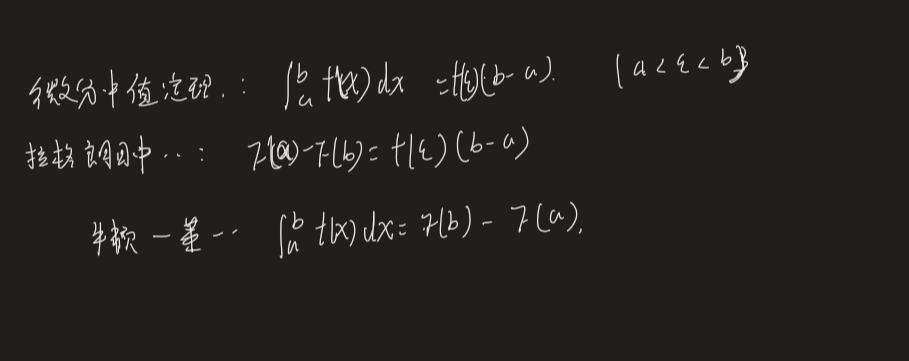



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本
· C#/.NET/.NET Core优秀项目和框架2025年2月简报
· Manus爆火,是硬核还是营销?
· 终于写完轮子一部分:tcp代理 了,记录一下
· 【杭电多校比赛记录】2025“钉耙编程”中国大学生算法设计春季联赛(1)