Dijkstra最短路径算法

概念

是从一个顶点到其余各顶点的最短路径算法，解决的是有权图中最短路径问题。迪杰斯特拉算法主要特点是从起始点开始，采用贪心算法的策略，每次遍历到始点距离最近且未访问过的顶点的邻接节点，直到扩展到终点为止 百度

时间

\(O(N^2)\)

代码实现

思想：对于连通图，先创建访问节点，图转临界矩阵,由源点到目标节点，每次在数组中变量
如果是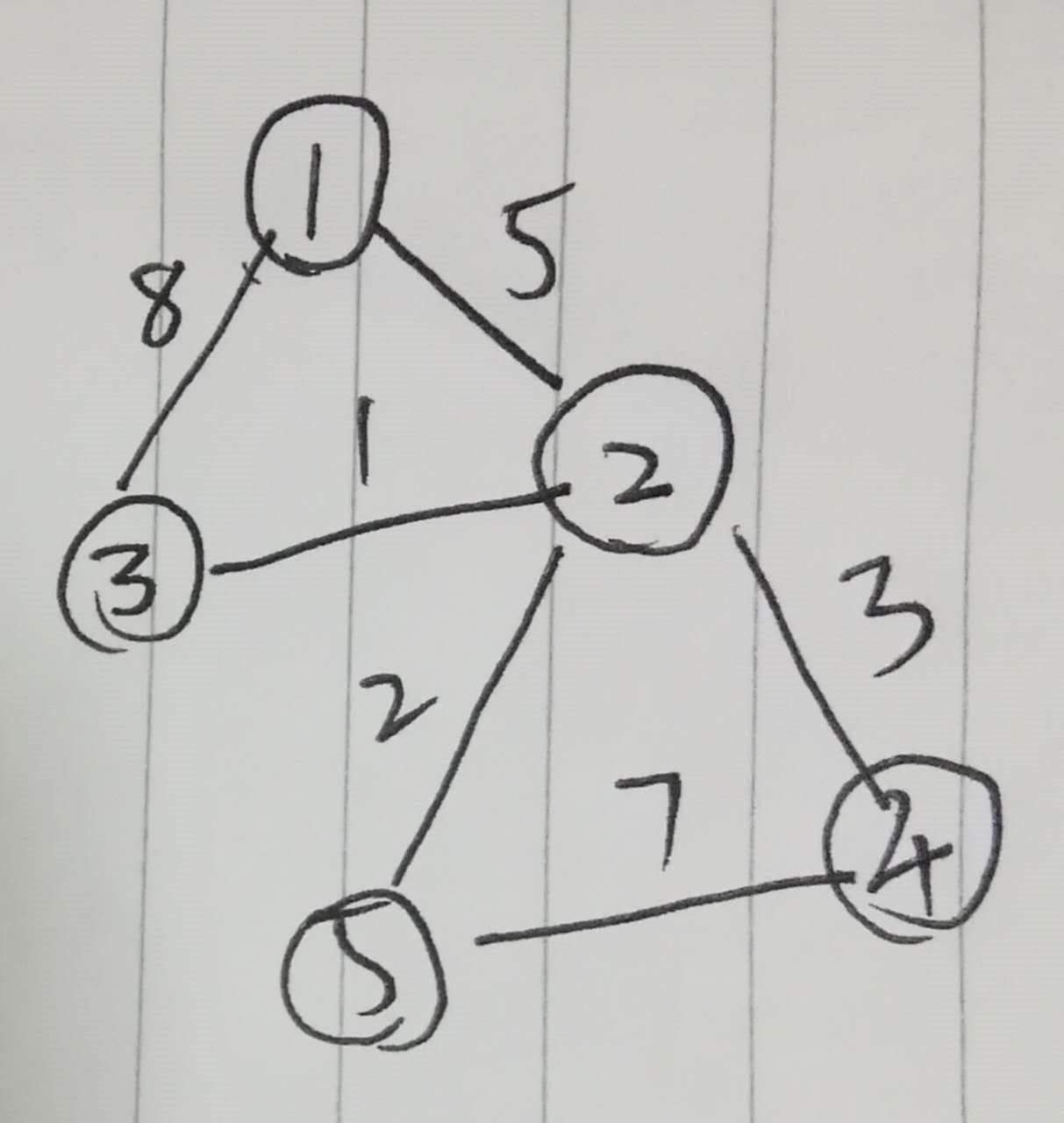

• 源点假设为1号，建立数组{0，5，8，M，M}其中M表示很大，以为和源点不直接联通
• 然后在数组中选出和源点最近的点，这里是2点，在以2为源点，并且标记数组2号为已经 访问更新数组{0，5，6，8，7}...

#include<stdio.h>
#include<stdlib.h>
#define max1 10000000  //原词条这里的值太大，导致溢出，后面比较大小时会出错
int a[1000][1000];
int d[1000];//d表示源节点到该节点的最小距离
int p[1000];//p标记访问过的节点
int i, j, k;
int m;//m代表边数
int n;//n代表点数
int main()
{
    scanf("%d%d",&n,&m);
    int    min1;
    int    x,y,z;
    for(i=1;i<=m;i++)
    {
        scanf("%d%d%d",&x,&y,&z);
        a[x][y]=z;
        a[y][x]=z;
    }
    for( i=1; i<=n; i++)
        d[i]=max1;
    d[1]=0;
    for(i=1;i<=n;i++)
    {
        min1 = max1;
        //下面这个for循环的功能类似冒泡排序，目的是找到未访问节点中d[j]值最小的那个节点，
        //作为下一个访问节点，用k标记
        for(j=1;j<=n;j++)
            if(!p[j]&&d[j]<min1)
            {
                min1=d[j];
                k=j;
            }
        //p[k]=d[k]; // 这是原来的代码，用下一 条代码替代。初始时，执行到这里k=1，而d[1]=0
       //从而p[1]等于0，这样的话，上面的循环在之后的每次执行之后，k还是等于1。
        p[k] = 1; //置1表示第k个节点已经访问过了
        for(j=1;j<=n;j++)
            if(a[k][j]!=0&&!p[j]&&d[j]>d[k]+a[k][j])
                d[j]=d[k]+a[k][j];
    }
    //最终输出从源节点到其他每个节点的最小距离
    for(i=1;i<n;i++)
        printf("%d->",d[i]);
    printf("%d\n",d[n]); 
    return 0;
}

参考

博客园