哈夫曼树

概念

给定N个权值作为N个叶子结点，构造一棵二叉树，若该树的带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近。
百度

什么是带权路径？

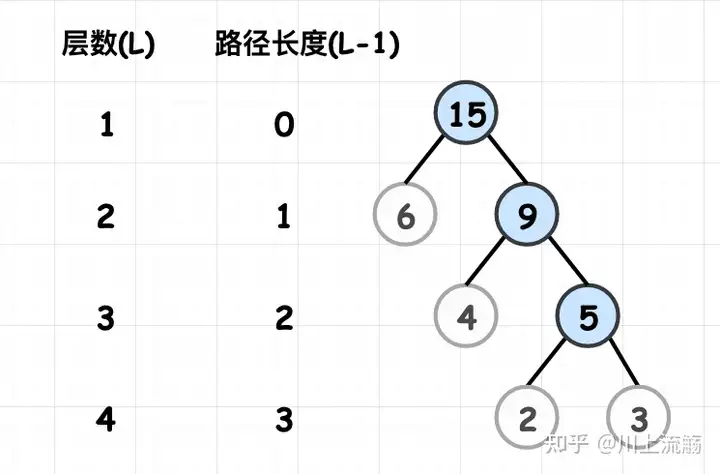
首先权是每个节点的值，路径就是根节点到到下面层的路径
WPL = 路径长度*节点权值 的总和

建立

对于多个节点，选择先选两个权值小的节点，然后建立树，得到父亲节点是（选出的两个子节点的和）将两个子节点移除，将新建立的父亲节点加入，又重复上述

具体代码实现

双指针法

void huffman(int* arrays,int size){
    int n = size;
    //双指针
    int left = 0,right = 1;
    int sum = 0;
    cout<<"n:"<<n<<endl;
    while(right<n){
        sort(arrays+left,arrays+n);
         sum = arrays[left]+arrays[right];//选出两个两个小值
         arrays[right] = sum;//覆盖较小的内存地址，后面又会排序
         left = right;
         right++;
         }
    }
    cout<<"ans: "<<arrays[n-1];
}
int main(){
    int n ;
    
    cin>>n;
    int arrays[n];
    for(int i = 0;i<n;i++){
       cin>>arrays[i];
    }
    huffman(arrays,n);
}

//具体就是每次选出当前数组的两个最小值，也可以用全局变量标记

参考

哈夫曼树

知乎