先验分布：（二）选取先验概率分布

一、结合实际应用

之前讲到，当不知道原因的概率的时候，可以选取一种相对灵活的概率分布表示先验概率的分布。

而选取哪种分布往往取决于实际应用或问题是什么。

 

在继续介绍该如何选取分布类型之前，我们先以一个简单的例子描述一下我们需要解决的问题：

假设有两枚硬币C1和C2，C1硬币抛出正面的概率是0.6，C2硬币抛出正面的概率是0.3。现在，我们做一个实验：

每次取两枚硬币中的一枚，抛出这枚硬币，连抛10次，记录正面和反面出现的次数。此为1次试验。我们做5次。实验结果如下：

试验编号	所用硬币	试验结果
1	？	5+:5-
2	？	6+:4-
3	？	3+:7-
4	？	4+:6-
5	？	6+:4-

先不管所用硬币是哪枚，单单就试验结果而言，试验结果是服从二项分布的，即每一次抛硬币的结果非正即反。

然而，实际的情况是，试验中所用硬币对试验结果是有影响的，因为两枚硬币抛出正面的概率是不一样的。因此，试验结果可以看作是先选取硬币，再抛选到的硬币。也就是说，选硬币是原因，试验结果是这个原因所导致的结果。

 

现在，我们要根据这5次试验结果推断每次试验用的是哪枚硬币。

现在的情况是，我们不知道选到哪枚硬币的概率是多少，即选取硬币的概率未知。

为了推断每次试验用的是哪枚硬币，我们需要根据试验结果倒推，寻找能让这5次试验结果——这一组合出现概率最大的那个选硬币的概率。如此，我们就有充分的信心相信，要使这5次试验结果的组合的出现概率最大，每次试验之前应该选哪枚硬币。

既然是倒推，就需要设定一个初始的选硬币的概率（先验概率），然后再根据倒推的结果（后验概率）调整选硬币的概率，这个过程可表示为：

设选到硬币的事件为θ，每次试验硬币朝上的次数为X。

先假定选硬币的概率（如选到C1的概率为0.7，即p(θ=C1) = 0.7）

　　→ 计算在已经选到硬币的基础上，在一次试验中出现X = 5的概率p(X=5|θ=C1)，此即为似然函数的值

　　　　→ 根据公式：后验概率 = 似然函数 × 先验概率，计算在X = 5的情况下，选到的硬币是C1的概率，

　　　　    表示为p(θ=C1|X=5)，即后验概率

　　　　　　→ 根据这个后验概率调整（或替代）之前的先验概率

 

事实上，在很多情况下，通过上述步骤得到的后验概率并不是最理想的结果，也就是说，如果用这个后验概率作为先验概率，再一次通过上述步骤计算出第二个后验概率，如果通过某些度量，发现第二个后验概率比第一个后验概率更好，则应该用第二个后验概率调整（或替代）第一个后验概率。这个过程一直要持续到新得到的后验概率不再变化（即收敛）。

那么，问题就来了：凭什么后验概率可以调整（或替代）先验概率？事实上，只要后验概率的范围仍然在(0, 1)之间，它就可以作为新的先验概率继续参与新的后验概率的计算。

不过，要注意的是，先验概率和后验概率不一定都在同一个（即分布的参数都相同）分布上。更多的情况是，后验概率在不同的分布上。理想的情况是，先验概率和后验概率有同样形式的分布，只是参数不同（即形状不同）。

很激动的是，就有这么一个分布，定义了(0, 1)之间的连续分布，有两个参数控制分布的形状，它就是Beta分布。

 

Beta分布根据其参数α和β的不同，有各种各样的形状（如下图所示），但符合该分布的变量取值总是在(0, 1)之间。

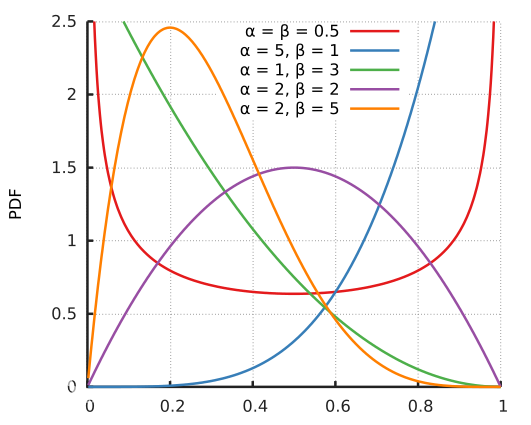
（概率密度函数）

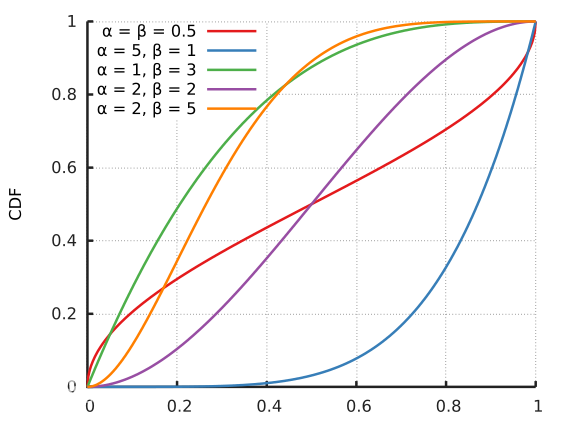
（累积函数）

 

二、从一维到多维

上面说到的Beta分布定义的是1个事件的先验概率的分布，比如抛硬币正面向上的事件概率。

在实际应用中，我们有时候会不清楚多个事件中各个事件的概率，比如掷一枚不均匀6面骰子，分别出现数字1-6的概率。这时候，因为实验结果服从多项分布，就不能用Beta分布了，而需要改用定义多个均位于(0, 1)区间变量的概率分布。

数学上已经证明，可用狄利克雷分布(Dirichlet Distribution)——Beta分布在多维上的扩展来表示多个未知概率事件的概率分布。