WPF制作带明细的环形图表

效果

明细用Popup实现的,录gif时,Popup显示不出来,不知道为什么,所以静态图凑合看吧

大体思路

图表使用Arc+Popup实现

图表分为两部分,一是环形部分,一是标注的明细部分.

环形部分使用Arc图形表示.需要注意这个Arc是Blend里的图形.用Blend建项目的话可以直接用,使用VS建项目需要添加引用 Microsoft.Expression.Drawing 在引用管理器=>程序集=>扩展 下(前提是已经安装了Blend)

明细部分使用Popup控件,IsOpen属性绑定到Arc的IsMouseOver,也就是鼠标进入圆弧的时候,Popup就打开显示.

Popup内部一个椭圆控件当作背景,一个文字显示,一个折线虚线化当作指针

然后就是把Popup定位到对应圆弧合适的位置去显示(这里取的是圆弧的中间)

比较抱歉的是样式比较丑陋,忽略吧,重点看定位.

圆弧部分

Arc有两个重要的属性:StartAngle起始角度和EndAngle终结角度.这两个属性决定了圆弧占所在圆环的比例.

每一个数据项就对应一个圆弧,把所有圆弧都放到一个容器里,首尾相连

数据项的总和为100,那么所有圆弧也就组成一个完整的圆环.

Popup明细部分

明细部分分为四种,见图

椭圆

从图可知,作为背景的椭圆分为两种情况,小于180度,椭圆靠容器的右边对齐,大于180度,靠容器的左边对齐

也就是代码的这部分:

Ellipse ell = new Ellipse() { Fill = brush };
//中间点角度小于180 明细靠右显示 否则靠左显示
Grid detailGrid = new Grid() { Width = _popupHeight, HorizontalAlignment = HorizontalAlignment.Right };
if (middleAngle > 180)
{
    detailGrid.HorizontalAlignment = HorizontalAlignment.Left;
}

折线

折线是分为四种,每一个角度区间都对应一种

private Polyline GetPopupPolyline(double middleAngle)
{
    Polyline pLine = new Polyline() { Stroke = new SolidColorBrush(Color.FromRgb(0, 0, 0)), StrokeDashArray = new DoubleCollection(new double[] { 5, 2 }) };
    double x1 = 0, y1 = 0;
    double x2 = 0, y2 = 0;
    double x3 = 0, y3 = 0;
    if (middleAngle > 0 && middleAngle <= 90)
    {
        x1 = 0; y1 = _popupHeight;
        x2 = _popupWidth / 2; y2 = _popupHeight;
        x3 = _popupWidth * 3 / 4; y3 = _popupHeight / 2;
    }
    if (middleAngle > 90 && middleAngle <= 180)
    {
        x1 = 0; y1 = 0;
        x2 = _popupWidth / 2; y2 = 0;
        x3 = _popupWidth * 3 / 4; y3 = _popupHeight / 2;
    }
    if (middleAngle > 180 && middleAngle <= 270)
    {
        x1 = _popupWidth; y1 = 0;
        x2 = _popupWidth / 2; y2 = 0;
        x3 = _popupWidth / 4; y3 = _popupHeight / 2;
    }
    if (middleAngle > 270 && middleAngle <= 360)
    {
        x1 = _popupWidth; y1 = _popupHeight;
        x2 = _popupWidth / 2; y2 = _popupHeight;
        x3 = _popupWidth / 4; y3 = _popupHeight / 2;
    }
    pLine.Points.Add(new Point(x1, y1));
    pLine.Points.Add(new Point(x2, y2));
    pLine.Points.Add(new Point(x3, y3));
    return pLine;
}

Popup的定位

首先以0-90度为例,说明一些基本的东西,见图

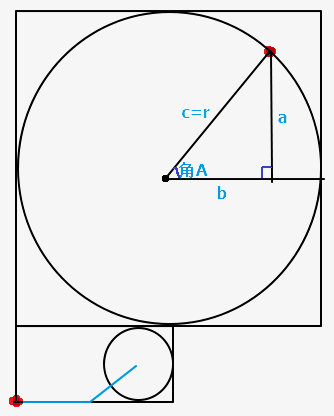
首先Popup默认的位置,都是在它容器的左下方的,Popup的左上角和容器的左下角重合.

现在要做的是Popup标记为红点的位置,和圆环上标记为红点的位置重合.

先来回顾一下小时候学过的公式:

1.直角三角形 a=r*sinA

2.勾股定理 c^2=a^2+b^2 b=Sqrt(c^2-a^2)

上图的直角三角形,角A的对边为a,临边为b,斜边为c.显然c边于圆的半径r相等.注意:因为圆弧是有厚度的,所以取r的时候要减去二分之一的圆弧厚度.

角A是可以通过90度减去圆弧的对应的角度求出来的,也就是sinA的值已知了,那么就可以求出a和b的长度,然后就可以去移动Popup了

一.0-90度

X轴:1.向右移动二分之一个容器的width 2.向右移动一个b的距离

Y轴:1.向上移动二分之一个容器的height 2.向上移动一个Popup的height 3.向上移动一个a的距离

二.90-180度

X轴:1.向右移动二分之一个容器的width 2.向右移动一个a的距离

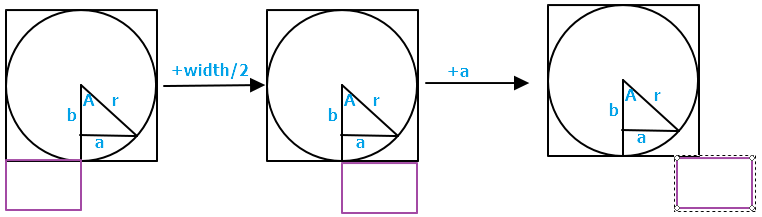
Y轴:1.上移二分之一个圆弧的Thickness,以保证标记的起点在圆弧的中央 2.上移一个(r-b)的距离

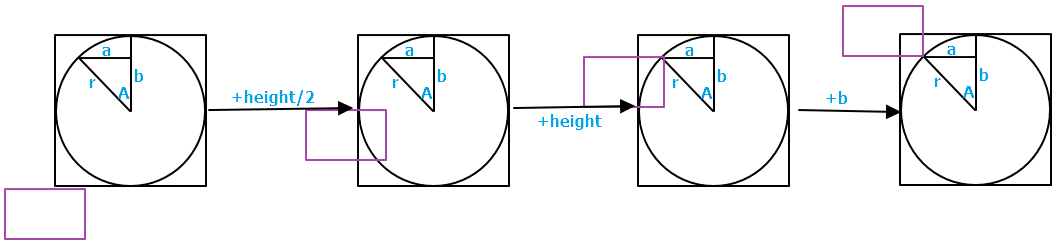
三.180-270度

X轴:1.向左移动一个b的距离

Y轴:1.上移二分之一个圆弧的Thickness,以保证标记的起点在圆弧的中央 2.上移一个(r-a)的距离

四.270-360度

X轴:1.向左移动一个a的距离

Y轴:1.向上移动二分之一个容器的height 2.向上移动一个Popup的height 3.向上移动一个b的距离

代码部分

private Popup GetPopup(double middleAngle)
{
    /*
     * 生成popup
     * 设置popup的offset 让标记线的起点 对应到圆弧的中间点
     */
    Popup popup = new Popup() { Width = _popupWidth, Height = _popupHeight, AllowsTransparency = true, IsHitTestVisible = false };
    //直角三角形 a=r*sinA 勾股定理 c^2=a^2+b^2 b=Sqrt(c^2-a^2)
    double r = _chartSize / 2 - _arcThickness / 2;
    double offsetX = 0, offsetY = 0;
    if (middleAngle > 0 && middleAngle <= 90)
    {
        double sinA = Math.Sin(Math.PI * (90 - middleAngle) / 180);
        double a = r * sinA;
        double c = r;
        double b = Math.Sqrt(c * c - a * a);
        offsetX = _chartSize / 2 + b;
        offsetY = -(_chartSize / 2 + _popupHeight + a);
    }
    if (middleAngle > 90 && middleAngle <= 180)
    {
        double sinA = Math.Sin(Math.PI * (180 - middleAngle) / 180);
        double a = r * sinA;
        double c = r;
        double b = Math.Sqrt(c * c - a * a);
        offsetX = _chartSize / 2 + a;
        offsetY = -(_arcThickness / 2 + (r - b));
    }
    if (middleAngle > 180 && middleAngle <= 270)
    {
        double sinA = Math.Sin(Math.PI * (270 - middleAngle) / 180);
        double a = r * sinA;
        double c = r;
        double b = Math.Sqrt(c * c - a * a);
        offsetX = -_popupWidth + (r - b) + _arcThickness / 2;
        offsetY = -(_arcThickness / 2 + (r - a));
    }
    if (middleAngle > 270 && middleAngle <= 360)
    {
        double sinA = Math.Sin(Math.PI * (360 - middleAngle) / 180);
        double a = r * sinA;
        double c = r;
        double b = Math.Sqrt(c * c - a * a);
        offsetX = -_popupWidth + (r - a) + _arcThickness / 2;
        offsetY = -(_chartSize / 2 + _popupHeight + b);
    }
    popup.HorizontalOffset = offsetX;
    popup.VerticalOffset = offsetY;

    return popup;
}

 

差不多主要的就是这些了.到这.画图有点累.

源码下载:ArcChart.zip

 

2017-07-13更新:

昨天刚发了博客,今天就发现了bug,真尴尬.180-270度和270-360度的算法有问题,由于例子选用尺寸的问题,早时没有发现.

正确的算法:

180-270度:

X轴:1.向左移动一个Popup的Width 2.向右移动一个(r-b)的距离 3.向右移动二分之一个ArcThickness的距离

Y轴不变

270-360度:

X轴:1.向左移动一个Popup的Width 2.向右移动一个(r-a)的距离 3.向右移动二分之一个ArcThickness的距离

Y轴不变

源码已更新,欢迎重新下载