不同智能优化算法如何进行性能分析比较？

 

不同智能优化算法如何进行性能分析比较？

 

智能优化算法一类随机优化算法，算法每次执行结果略有差异， 该类算法通常通过模仿现实生活中的某种行为机制的方式而被提出，不同种类的算法优化机理不同，即使同一算法及其改进算法在搜索机理上也往往存在很大差别。对于搜索性能稳定的算法这种差异相对较小，而对于搜索性能波动较大的算法每次执行结果差异较为明显。如何衡量算法间的优劣呢？为此，学术界提出了多种不同的算法性能评价基准，其中较为典型的就是国际进化计算会议提出的CEC系列基准测试函数，通过重复测试算法寻找函数全局最优值的相关数据统计值实现对算法的性能评估。当前主要的数据统计指标包括：均值，方差，最大值，最小值，中位数值。

在算法实验测试过程中，我们首先假定待评估的算法为A，算法评估测试函数选定为F1,F2,…,F10。

 

首先，对于测试函数F1,算法A重复运行R轮，每一轮循环迭代次数为T，在每轮迭代过程中记录每一代搜索到的全局最优适应度数值，并记录为bf1,bf2,…,bf_t.那么本次迭代过程中全局最优适应度数值等于最后的bf_t(因为搜索迭代的过程就是逐步逼近最优的过程，长江后浪推前浪，一代总比一代强~)。如下图

 

 

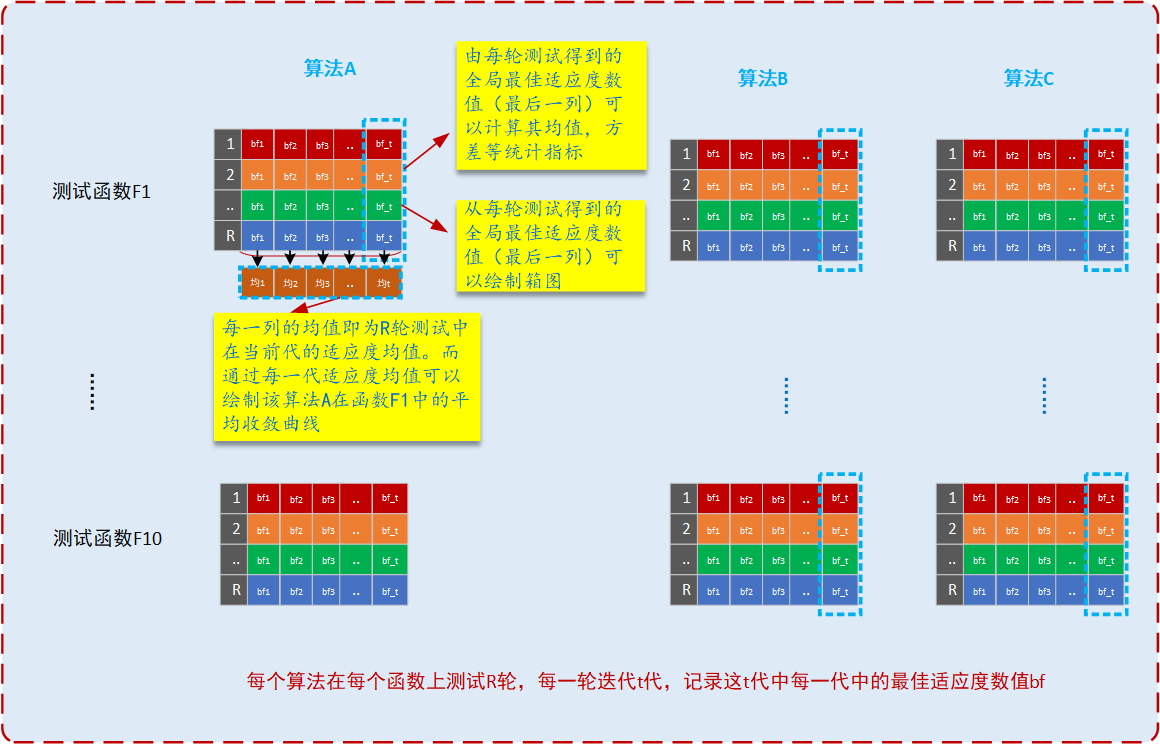
然后，继续重复测试得到类似的数据。同理，对于算法B，记录与算法A相同的数据。基于上述数据我们就可以得到R轮测试中的各种统计指标，其中包括最佳适应度数值的均值mean，标准方差std，最大值Max，最小值Min，绘制各算法的收敛曲线Convergence curve，绘制算法的统计箱图Boxplot（直截了当看出两种或多种算法在某函数上搜索的性能高低）。根据统计数值结果如何判断算法A和算法B的优劣呢？这就需要通过统计的方法进行分析，通过假设检验的方法判断在某个函数上，算法A的搜索性能优于B具有显著性或算法A搜索性能次于B具有显著性，或者A和B搜索性能相当在统计学意义上具有显著性。假设检验的方法有很多(无参的检验，有参的检验)，其中较为典型的统计检验方法包括：t检验方法，wilcoxn秩和检验方法。