神经网络与深度学习（2）：梯度下降算法和随机梯度下降算法
本文总结自《Neural Networks and Deep Learning》第1章的部分内容。
使用梯度下降算法进行学习（Learning with gradient descent）
1. 目标
我们希望有一个算法，能让我们找到权重和偏置，以至于网络的输出y(x) 能够拟合所有的训练输入x。
2. 代价函数（cost function）
定义一个Cost function (loss function, objective function): 目标函数，如下：
C: 被称为二次代价函数；有时也被称为均方误差或者MSE
w: weight 权重
b: bias 偏向
n: 训练数据集实例个数
x: 输入值
a: 输出值 (当x是输入时)
||v||: 向量v的模
C(w,b) 越小越好，输出的预测值和真实值差别越小越好。
那么我们的目标就转为： 最小化C(w,b)。
我们训练神经网络的目的是找到能最小化二次代价函数C(w; b) 的权重和偏置。
3. 梯度下降
最小化问题可以用梯度下降解决（gradient descent)。
C(v) v有两个变量v1, v2，通常可以用微积分解决，如果v包含的变量过多，无法用微积分解决。
梯度下降算法工作的方式就是重复计算梯度∇C，然后沿着相反的方向移动，沿着山谷“滚落”。
即每下降到一个地方，就要计算下一步要往哪个方向下去。
权重和偏置的更新规则：
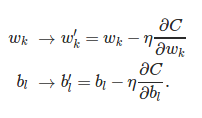
4. 随机梯度下降算法 (stochastic gradient descent)
实际中使用梯度下降算法会使学习变得相当缓慢。这是因为：
对于每个训练实例x, 都要计算梯度向量∇C。如果训练数据集过大，会花费很长时间，学习过程太慢。
所以实际中使用随机梯度下降算法 (stochastic gradient descent)。
基本思想: 从所有训练实例中取一个小的采样(sample): X1,X2,…,Xm (mini-batch)，来估计 ∇C, 大大提高学习速度。
如果样本够大，
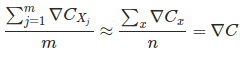
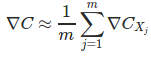
代入更新方程：
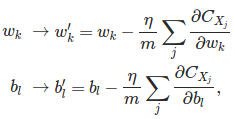
然后，重新选择一个mini-batch用来训练，直到用完所有的训练实例，一轮epoch完成。
作者：tsianlgeo
本文版权归作者和博客园共有，欢迎转载，未经同意须保留此段声明，且在文章页面明显位置给出原文链接。欢迎指正与交流。
