recastnavigation计算三角形离给定点最近位置方法简单注释
三角形
在recastnavigation中，三角形是最基础的元素，很多逻辑都是基于三角形进行的，其中比较常见的一个操作就是计算指定点到某三角形上的最近距离。由于三角形通常代表行走面，而给定点P可能是场景中的任意位置，所以这个操作通常会用来计算可行走面的最近距离。
recastnavigation的计算
主体代码在dtClosestPtPointTriangle函数，代码风格一直简洁明快，但是注释也说明了关键思路和步骤。
void dtClosestPtPointTriangle(float* closest, const float* p,
const float* a, const float* b, const float* c)
{
// Check if P in vertex region outside A
float ab[3], ac[3], ap[3];
dtVsub(ab, b, a);
dtVsub(ac, c, a);
dtVsub(ap, p, a);
float d1 = dtVdot(ab, ap);
float d2 = dtVdot(ac, ap);
if (d1 <= 0.0f && d2 <= 0.0f)
{
// barycentric coordinates (1,0,0)
dtVcopy(closest, a);
return;
}
// Check if P in vertex region outside B
float bp[3];
dtVsub(bp, p, b);
float d3 = dtVdot(ab, bp);
float d4 = dtVdot(ac, bp);
if (d3 >= 0.0f && d4 <= d3)
{
// barycentric coordinates (0,1,0)
dtVcopy(closest, b);
return;
}
// Check if P in edge region of AB, if so return projection of P onto AB
float vc = d1*d4 - d3*d2;
if (vc <= 0.0f && d1 >= 0.0f && d3 <= 0.0f)
{
// barycentric coordinates (1-v,v,0)
float v = d1 / (d1 - d3);
closest[0] = a[0] + v * ab[0];
closest[1] = a[1] + v * ab[1];
closest[2] = a[2] + v * ab[2];
return;
}
// Check if P in vertex region outside C
float cp[3];
dtVsub(cp, p, c);
float d5 = dtVdot(ab, cp);
float d6 = dtVdot(ac, cp);
if (d6 >= 0.0f && d5 <= d6)
{
// barycentric coordinates (0,0,1)
dtVcopy(closest, c);
return;
}
// Check if P in edge region of AC, if so return projection of P onto AC
float vb = d5*d2 - d1*d6;
if (vb <= 0.0f && d2 >= 0.0f && d6 <= 0.0f)
{
// barycentric coordinates (1-w,0,w)
float w = d2 / (d2 - d6);
closest[0] = a[0] + w * ac[0];
closest[1] = a[1] + w * ac[1];
closest[2] = a[2] + w * ac[2];
return;
}
// Check if P in edge region of BC, if so return projection of P onto BC
float va = d3*d6 - d5*d4;
if (va <= 0.0f && (d4 - d3) >= 0.0f && (d5 - d6) >= 0.0f)
{
// barycentric coordinates (0,1-w,w)
float w = (d4 - d3) / ((d4 - d3) + (d5 - d6));
closest[0] = b[0] + w * (c[0] - b[0]);
closest[1] = b[1] + w * (c[1] - b[1]);
closest[2] = b[2] + w * (c[2] - b[2]);
return;
}
// P inside face region. Compute Q through its barycentric coordinates (u,v,w)
float denom = 1.0f / (va + vb + vc);
float v = vb * denom;
float w = vc * denom;
closest[0] = a[0] + ab[0] * v + ac[0] * w;
closest[1] = a[1] + ab[1] * v + ac[1] * w;
closest[2] = a[2] + ab[2] * v + ac[2] * w;
}
为了便于理解，简单画了一个示意图，图中1——6个区域分别对应了函数中的6个返回点(前5个return和最后一个自然退出)。
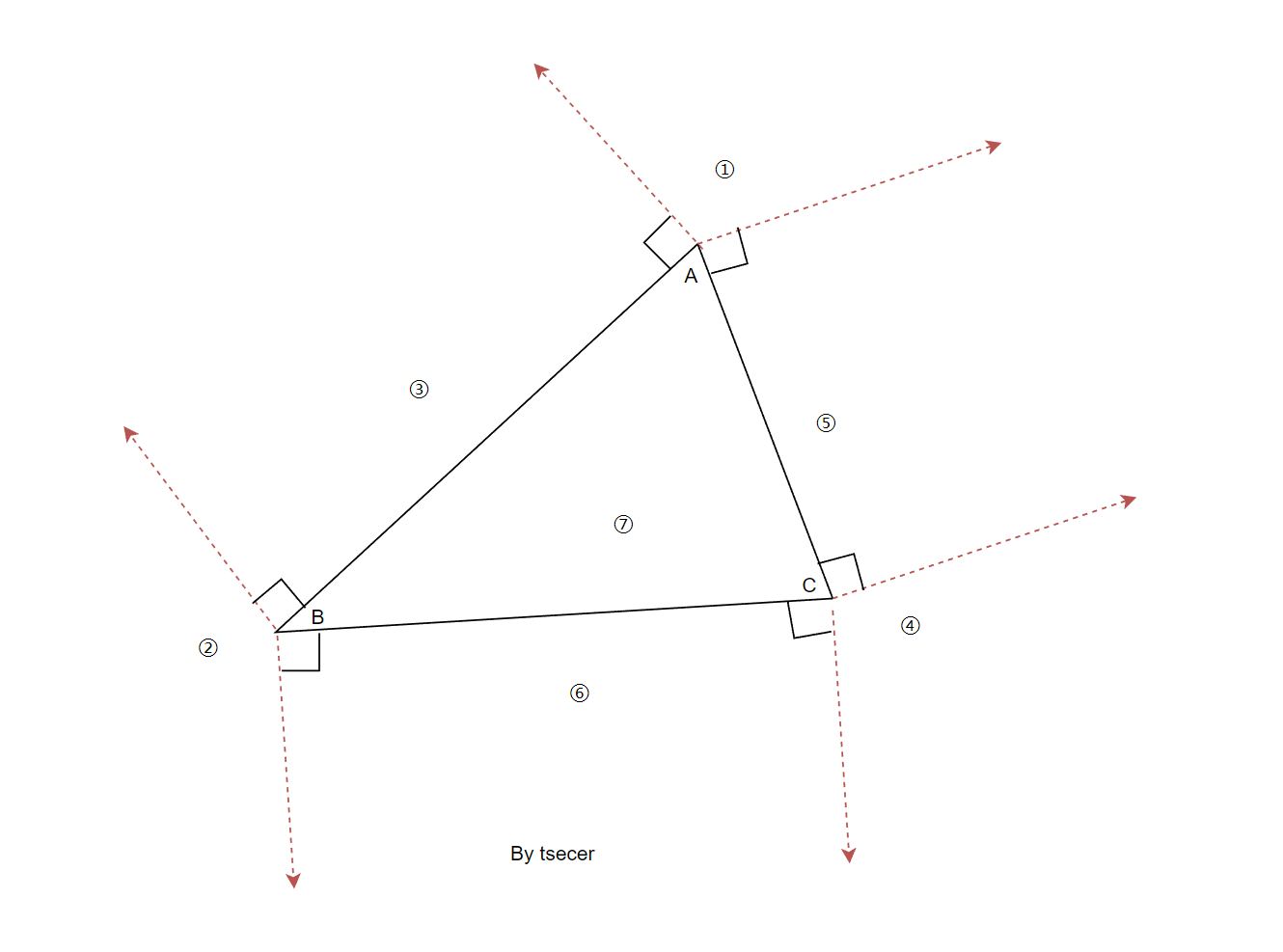
d1 <= 0.0f && d2 <= 0.0f
点乘有一个优良的几何性质，点乘的结果表示了两个向量夹角的cos值，该结果的正负表示了两个向量之间的夹角是否大于90度。如果点乘结果小于0，表示两个向量夹角大于90度。
这里另个判断表示点P在AB向量反方向，并且也在AC向量反方向，所以对应的就是图中的区域①。
d3 >= 0.0f && d4 <= d3
这里的 d4 <= d3 看起来不太直观：这个地方应该是P应该在CB向量的正方向，也就是CB*PB >= 0。
这里只是使用了一个简单的向量等式CB = (AB - AC) ，所以CB * PB >=0 等价于 (AB - AC) * PB >= 0 等价于 AB * PB >= AC * PB。
由于
float d3 = dtVdot(ab, bp);
并且
float d4 = dtVdot(ac, bp);
所以 AB * PB >= AC * PB <==> d3 >= d4。
vc <= 0.0f
一个基于极坐标的解释，由于网站规模比较小，文章数量也不多，恐怕哪天就不见了，所以还是整段全部拷贝过来。同样的问题，还有一个pdf格式的描述，看起来更舒服些。
The advantage of the method above is that it's very simple to understand so that once you read it you should be able to remember it forever and code it up at any time without having to refer back to anything. It's just - hey the point has to be on the same side of each line as the triangle point that's not in the line. Cake.
Well, there's another method that is also as easy conceptually but executes faster. The downside is there's a little more math involved, but once you see it worked out it should be no problem.
So remember that the three points of the triangle define a plane in space. Pick one of the points and we can consider all other locations on the plane as relative to that point. Let's go with A -- it'll be our origin on the plane. Now what we need are basis vectors so we can give coordinate values to all the locations on the plane. We'll pick the two edges of the triangle that touch A, (C - A) and (B - A). Now we can get to any point on the plane just by starting at A and walking some distance along (C - A) and then from there walking some more in the direction (B - A).
With that in mind we can now describe any point on the plane as
P = A + u * (C - A) + v * (B - A)
Notice now that if u or v < 0 then we've walked in the wrong direction and must be outside the triangle. Also if u or v > 1 then we've walked too far in a direction and are outside the triangle. Finally if u + v > 1 then we've crossed the edge BC again leaving the triangle.
Given u and v we can easily calculate the point P with the above equation, but how can we go in the reverse direction and calculate u and v from a given point P? Time for some math!
P = A + u * (C - A) + v * (B - A) // Original equation
(P - A) = u * (C - A) + v * (B - A) // Subtract A from both sides
v2 = u * v0 + v * v1 // Substitute v0, v1, v2 for less writing
// We have two unknowns (u and v) so we need two equations to solve
// for them. Dot both sides by v0 to get one and dot both sides by
// v1 to get a second.
(v2) . v0 = (u * v0 + v * v1) . v0
(v2) . v1 = (u * v0 + v * v1) . v1
// Distribute v0 and v1
v2 . v0 = u * (v0 . v0) + v * (v1 . v0)
v2 . v1 = u * (v0 . v1) + v * (v1 . v1)
// Now we have two equations and two unknowns and can solve one
// equation for one variable and substitute into the other. Or
// if you're lazy like me, fire up Mathematica and save yourself
// some handwriting.
Solve[v2.v0 == {u(v0.v0) + v(v1.v0), v2.v1 == u(v0.v1) + v(v1.v1)}, {u, v}]
u = ((v1.v1)(v2.v0)-(v1.v0)(v2.v1)) / ((v0.v0)(v1.v1) - (v0.v1)(v1.v0))
v = ((v0.v0)(v2.v1)-(v0.v1)(v2.v0)) / ((v0.v0)(v1.v1) - (v0.v1)(v1.v0))
Here's an implementation in Flash that you can play with. :)
// Compute vectors
v0 = C - A
v1 = B - A
v2 = P - A
// Compute dot products
dot00 = dot(v0, v0)
dot01 = dot(v0, v1)
dot02 = dot(v0, v2)
dot11 = dot(v1, v1)
dot12 = dot(v1, v2)
// Compute barycentric coordinates
invDenom = 1 / (dot00 * dot11 - dot01 * dot01)
u = (dot11 * dot02 - dot01 * dot12) * invDenom
v = (dot00 * dot12 - dot01 * dot02) * invDenom
// Check if point is in triangle
return (u >= 0) && (v >= 0) && (u + v < 1)
但是无论如何，两者说明的内容都是和代码中的不完全相同，不过也只是格式不同，本质是一样的，遗憾的是我还是没办法理解这种实现的直观(intuitive)解释:-(。
想让recastnavigation和文档中的内容相同，只需要做简单的向量转换即可，把代码中的BP根据向量减法替换为(AP - AB)，然后带入
const float vc = d1*d4 - d3*d2;
d1d4 - d3d2 = (ABAP) * (ACBP) - (AB * BP) * (AC * AP) = AB * AP (AC * (AP - AB)) - (AB * (AP - AB)) * AC * AP = AB * AP * AC * AP - AB * AP * AC * AB - AB * AP * AC * AP + AB * AB * AC * AP
由于第1项和第3项内容相同，符号相反，所以可以抵消掉，剩余内容为
-AB * AP * AC * AB + AB * AB * AC * AP = AB * AB * AC * AP - AB * AP * AC * AB = dot11 * dot02 - dot12 * dot01
由于点乘双方顺序无关，所以上面值和前面的u值相同。
根据u的定义，P点一定是在AC的反方向分量上(加上另一个ABv分量，无论这个ABv分量是多少，P一定在AB的外侧：因为P点是通过两个基向量AC和AB与U和v标量获得，也就是沿AC移动u然后再沿着AB移动v个距离)，所以在AB的外侧。
另外，embree库的closestPointTriangle函数实现，PhysX库也都使用了相同的方法。
UE的实现
UE的实现比较直观，就是计算垂线，然后判断方向，这个是最直观的实现方法，也最容易理解。
FVector FMath::ClosestPointOnTriangleToPoint(const FVector& Point, const FVector& A, const FVector& B, const FVector& C)
{
//Figure out what region the point is in and compare against that "point" or "edge"
const FVector BA = A - B;
const FVector AC = C - A;
const FVector CB = B - C;
const FVector TriNormal = BA ^ CB;
// Get the planes that define this triangle
// edges BA, AC, BC with normals perpendicular to the edges facing outward
const FPlane Planes[3] = { FPlane(B, TriNormal ^ BA), FPlane(A, TriNormal ^ AC), FPlane(C, TriNormal ^ CB) };
int32 PlaneHalfspaceBitmask = 0;
//Determine which side of each plane the test point exists
for (int32 i=0; i<3; i++)
{
if (Planes[i].PlaneDot(Point) > 0.0f)
{
PlaneHalfspaceBitmask |= (1 << i);
}
}
FVector Result(Point.X, Point.Y, Point.Z);
switch (PlaneHalfspaceBitmask)
{
case 0: //000 Inside
return FVector::PointPlaneProject(Point, A, B, C);
case 1: //001 Segment BA
Result = FMath::ClosestPointOnSegment(Point, B, A);
break;
case 2: //010 Segment AC
Result = FMath::ClosestPointOnSegment(Point, A, C);
break;
case 3: //011 point A
return A;
case 4: //100 Segment BC
Result = FMath::ClosestPointOnSegment(Point, B, C);
break;
case 5: //101 point B
return B;
case 6: //110 point C
return C;
default:
UE_LOG(LogUnrealMath, Log, TEXT("Impossible result in FMath::ClosestPointOnTriangleToPoint"));
break;
}
return Result;
}
