NOI2023春测题解

NOI2023春测题解

目录

更好的阅读体验戳此进入

游记戳此进入

T1 LG-P9117 [春季测试 2023] 涂色游戏

题面

给定矩阵，多次操作整行推平或整列推平，最后查询整个矩形。

Solution

给每行每列维护一个最后的推平并标记时间戳，查询时取行列最晚的推平作为答案即可。

考虑如果行列的区间推平以及随时查询并且强制在线，可以考虑对每行每列共 $ n + m $ 个 ODT，同时记录时间戳，这样复杂度应该也是正确的。

Code

#define _USE_MATH_DEFINES
#include <bits/stdc++.h>

#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW void* Edge::operator new(size_t){static Edge* P = ed; return P++;}
#define ROPNEW_NODE void* Node::operator new(size_t){static Node* P = nd; return P++;}

using namespace std;

mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}

typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;

template < typename T = int >
inline T read(void);

int N, M, Q;
pair < int, int > lstx[110000], lsty[110000];

int main(){
    int T = read();
    while(T--){
        memset(lstx, 0, sizeof lstx), memset(lsty, 0, sizeof lsty);
        N = read(), M = read(), Q = read();
        for(int i = 1; i <= Q; ++i){
            int opt = read(), p = read(), v = read();
            if(opt == 0)lstx[p] = {v, i};
            else lsty[p] = {v, i};
        }
        for(int i = 1; i <= N; ++i)
            for(int j = 1; j <= M; ++j)
                printf("%d%c", lstx[i].second > lsty[j].second ? lstx[i].first : lsty[j].first, j == M ? '\n' : ' ');
    }
    return 0;
}

template < typename T >
inline T read(void){
    T ret(0);
    int flag(1);
    char c = getchar();
    while(c != '-' && !isdigit(c))c = getchar();
    if(c == '-')flag = -1, c = getchar();
    while(isdigit(c)){
        ret *= 10;
        ret += int(c - '0');
        c = getchar();
    }
    ret *= flag;
    return ret;
}

T2 LG-P9118 [春季测试 2023] 幂次

题面

给定 $ n \(，\) k $，求在 $ [1, n] $ 中有多少数可以表示为 $ a^b $，其中 $ b \ge k $。

Solution

感觉差不多是绿题的难度，不卡精度的话应该算黄题难度，赛时的阴间思路在游记里了，这里说一下正解。

不难发现对于任意的合法的 $ b $，一定满足 $ a \le {^k\sqrt{n}} $，则对于 $ k \ge 3 $ 的情况，$ a $ 最大也是在 $ 10^6 $ 的范围，那么我们直接枚举所有的 $ a $，并枚举其所有合法的 $ a^b $，然后将其全部丢到 unordered_set 里，最后直接输出其 size() 即可，考虑这样的复杂度，显然枚举 $ a $ 是 $ O(n^{\frac{1}{k}}) $ 的，枚举幂次是 $ O(\log n) $ 的，则复杂度 $ O(n^{\frac{1}{k}} \log n) $，对于 $ k \ge 3 $ 的情况是随便过的。

考虑对于 $ k = 2 $ 的情况，不难发现这东西也是很显然的，枚举一下 unordered_set 中的所有数，若其为完全平方数的话贡献 $ -1 $，然后最后在答案中加上 $ \lfloor \sqrt{n} \rfloor $ 即可。不难发现此时复杂度为 $ O(n^{\frac{1}{3}} \log n) $，可以通过。

同时不难发现对于 $ \sqrt{n} $，这个东西如果直接朴素的用 double 的 sqrt() 函数的话会丢失精度，所以此时需考虑使用二分或 long double 或 __float128，前者会多一个 $ \log $，对于上述 $ k = 2 $ 的理论复杂度也是正确的。而用 __float128 会多一个十分巨大的甚至高于 $ \log $ 的常数，不建议使用。当然我们也可以朴素地使用 sqrt() 然后取其返回值一段较小的邻域进行验证，一般 $ \pm 1 $ 就够用了。

Code

#define _USE_MATH_DEFINES
#include <bits/stdc++.h>

#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW void* Edge::operator new(size_t){static Edge* P = ed; return P++;}
#define ROPNEW_NODE void* Node::operator new(size_t){static Node* P = nd; return P++;}

using namespace std;

mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}

typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;

template < typename T = int >
inline T read(void);

ll N, K;
unordered_set < ll > legal;
ll ans(0);

int main(){
    auto qpow_with_lim = [](ll a, ll b)->ll{
        ll ret(1), mul(a);
        while(b){
            if(b & 1)
                ret = (__int128_t)ret * mul > N ? N + 1 : ret * mul;
            b >>= 1;
            mul = (__int128_t)mul * mul > N ? N + 1 : mul * mul;
        }return ret;
    };

    N = read < ll >(), K = read();
    if(K == 1)printf("%lld\n", N), exit(0);
    legal.insert(1);
    for(ll i = 2; i <= (ll)1e6; ++i){
        auto cur = (__int128_t)qpow_with_lim(i, K == 2 ? 3 : K);
        while(cur <= N)
            legal.insert(cur), cur *= i;
    }ans += legal.size();
    if(K == 2){
        for(auto v : legal)
            if((ll)sqrt((ld)v) * (ll)sqrt((ld)v) == v)--ans;
        ans += (ll)floor(sqrt((ld)N));
    }printf("%lld\n", ans);
    fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
    return 0;
}

template < typename T >
inline T read(void){
    T ret(0);
    int flag(1);
    char c = getchar();
    while(c != '-' && !isdigit(c))c = getchar();
    if(c == '-')flag = -1, c = getchar();
    while(isdigit(c)){
        ret *= 10;
        ret += int(c - '0');
        c = getchar();
    }
    ret *= flag;
    return ret;
}

T3 LG-P9119 [春季测试 2023] 圣诞树

题面

给定平面内凸包，最小化从其最高点开始的任意哈密尔顿路径（认为任意两点之间均可到达）的欧几里得距离，输出最小化的方案。存在 SPJ。

Solution

首先对于 $ n \le 18 $，不难发现其为经典的 TSP 问题，状压后简单转移一下即可。对于性质 B，顺序输出即可。对于性质 A，目前没想到什么正确的思路。

考虑正解，发现对于任意两条路径一定不相交，证明是显然的，考虑任意四个点：

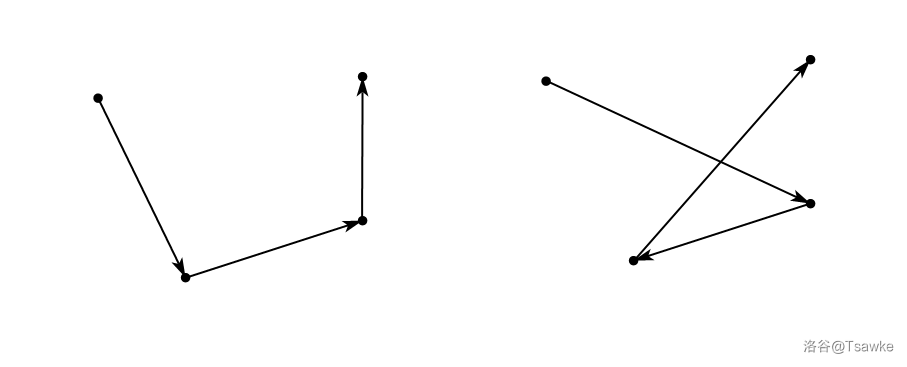
2023_03_06_1

显然由于三角形两边之和大于第三边，前者一定优于后者。

所以对于逆时针给定的若干个点，当处于 $ i $ 时，最优决策一定只能是下一步到 $ i - 1 $ 或 $ i + 1 $，否则将会存在一个点被隔离，导致最终去往该点时一定形成交叉路径。

于是此时问题显然地转化为了区间 DP，考虑将原序列倍长，设状态 $ dp(l, r, 0/1) $ 表示当前已经走过了 $ [l, r] $ 的点，且最后停在了 $ l $ 或 $ r $ 的最小的总距离，则显然对于起点 $ s $ 有 $ dp(s, s, 0) = 0, dp(s, s, 1) = 0 $。

转移也十分显然，与 [ABC273F] Hammer 2 类似，即：

\[dp(l, r, 0) = \min(dp(l + 1, r, 0) + dis(l + 1, l), dp(l + 1, r, 1) + dis(r, l) \]

\[dp(l, r, 1) = \min(dp(l, r - 1, 0) + dis(l, r), dp(l, r - 1, 1) + dis(r - 1, r)) \]

Code

#define _USE_MATH_DEFINES
#include <bits/stdc++.h>

#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW void* Edge::operator new(size_t){static Edge* P = ed; return P++;}
#define ROPNEW_NODE void* Node::operator new(size_t){static Node* P = nd; return P++;}

using namespace std;

mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}

typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;

template < typename T = int >
inline T read(void);

int N;
pair < ld, ld > pts[2100];
ld dis[2100][2100];
ld dp[2100][2100][2];
tuple < int, int, int > frm[2100][2100][2];
int top(-1); ld topy(-1e8);

int main(){
    auto CalDis = [](pair < ld, ld > a, pair < ld, ld > b)->ld{
        return sqrt((a.first - b.first) * (a.first - b.first) + (a.second - b.second) * (a.second - b.second));
    };
    auto Update = [](int l, int r, int k, int sl, int sr, int sk, int dl, int dr)->void{
        if(dp[sl][sr][sk] >= 1e12)return;
        if(dp[sl][sr][sk] + dis[dl][dr] < dp[l][r][k])
            dp[l][r][k] = dp[sl][sr][sk] + dis[dl][dr], frm[l][r][k] = {sl, sr, sk};
    };

    for(int i = 0; i <= 2010; ++i)for(int j = 0; j <= 2010; ++j)for(int k = 0; k <= 1; ++k)dp[i][j][k] = 1e12;
    N = read();
    for(int i = 1; i <= N; ++i){
        scanf("%Lf%Lf", &pts[i].first, &pts[i].second);
        pts[i + N] = pts[i];
        if(pts[i].second > topy)topy = pts[i].second, top = i;
    }
    for(int i = 1; i <= N; ++i)for(int j = 1; j <= N; ++j)
        dis[i][j] = dis[i + N][j] = dis[i][j + N] = dis[i + N][j + N] = CalDis(pts[i], pts[j]);
    dp[top][top][0] = dp[top][top][1] = dp[top + N][top + N][0] = dp[top + N][top + N][1] = 0.0;
    for(int len = 2; len <= N; ++len)
        for(int l = 1; l <= (N << 1) - len + 1; ++l){
            int r = l + len - 1;
            Update(l, r, 0, l + 1, r, 0, l + 1, l);
            Update(l, r, 0, l + 1, r, 1, r, l);
            Update(l, r, 1, l, r - 1, 0, l, r);
            Update(l, r, 1, l, r - 1, 1, r - 1, r);
        }
    ld ansv(1e12); tuple < int, int, int > curp(0, 0, 0);
    for(int l = 1; l < N; ++l){
        int r = l + N - 1;
        if(dp[l][r][0] < ansv)ansv = dp[l][r][0], curp = {l, r, 0};
        if(dp[l][r][1] < ansv)ansv = dp[l][r][1], curp = {l, r, 1};
    }
    basic_string < int > rans;
    auto [l, r, k] = curp;
    auto lst = curp; curp = frm[l][r][k];
    while(get < 0 >(curp)){
        auto [l, r, k] = lst;
        auto [cl, cr, ck] = curp;
        if(l != cl)rans += l;
        else rans += r;
        lst = curp;
        curp = frm[cl][cr][ck];
    }rans += get < 0 >(lst);
    for_each(rans.rbegin(), rans.rend(), [rans](auto val)->void{printf("%d%c", val > N ? val - N : val, val == *prev(rans.rend()) ? '\n' : ' ');});
    fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
    return 0;
}

template < typename T >
inline T read(void){
    T ret(0);
    int flag(1);
    char c = getchar();
    while(c != '-' && !isdigit(c))c = getchar();
    if(c == '-')flag = -1, c = getchar();
    while(isdigit(c)){
        ret *= 10;
        ret += int(c - '0');
        c = getchar();
    }
    ret *= flag;
    return ret;
}

T4 LG-P9120 [春季测试 2023] 密码锁

$ k = 1, k = 2 $ 十分朴素，$ k = 3 $ 考虑二分答案后钦定全局最大最小值的位置后枚举另外一列的值域解决，$ k = 4 $ 较为复杂略了。

UPD

update-2023_03_06 初稿

posted @ 2023-03-06 19:26  Tsawke  阅读(593)  评论(0)  编辑  收藏  举报