关于一些Trick以及一些定理与小技巧
关于一些Trick以及一些定理与小技巧
更好的阅读体验戳此进入
一个关于数位求和的性质
大概是这样:
\[\overline{a_1 a_2 a_3 \cdots a_n} \equiv \sum_{i = 1}^n a_i \pmod{9}
\]
证明显然,考虑转化一下即可:
\[\iff \sum_{i = 1}^n a_i \times 10^{n - i} \equiv \sum_{i = 1}^n a_i \pmod{9}
\]
两边各减去 $ \texttt{RHS} $ 得到:
\[\sum_{i = 1}^n a_i \times 999 \cdots 999 \equiv 0 \pmod{9}
\]
则显然成立。
同理对于 $ 3 $ 亦成立。
自然数幂次和
\[\sum_{i = 1}^n i^2 = \dfrac{n(n + 1)(2n + 1)}{6}
\]
\[\sum_{i = 1}^n i^3 = \left( \dfrac{n(n + 1)}{2} \right)^2
\]
手撕根号
大概思路先放个图片吧:

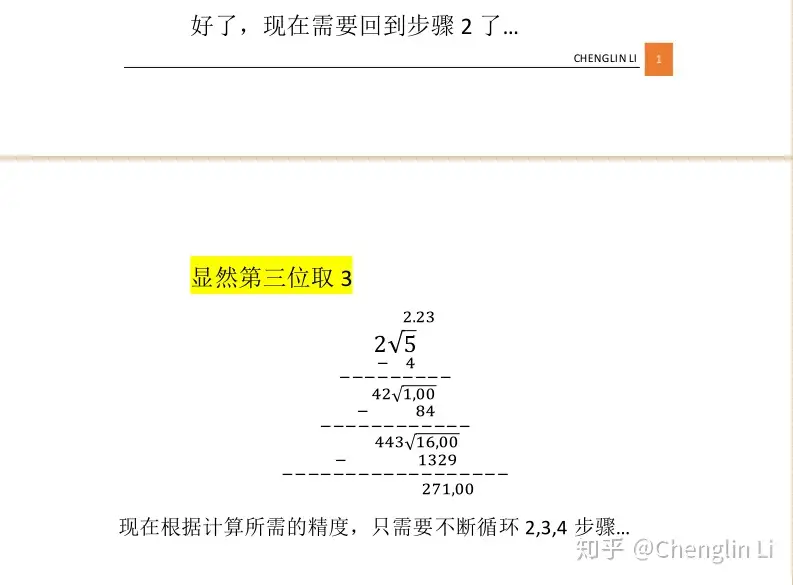
大概就是先除以 $ 2 $,令商为 $ a $,余数为 $ p $,商作为第一位整数位。然后令 $ p \times 100 $ 为新的值,令 $ a \times 20 $ 为基准,记作 $ \overline{(2a)x} $,我们要找到最接近但小于 $ 100 $ 的 $ \overline{(2a)x} \times x $,该 $ x $ 作为结果的第二位,然后不断循环即可。
UPD
update-2023_01_13 添加数位求和 手撕根号
update-2023_03_03 添加自然数幂次和

