浅析群论
Group Theory - 浅析群论
- Group Theory - 浅析群论
- 更好的阅读体验戳此进入
- 群
- 其它群
- 双半群模型
- 阶
- 子群
- 陪集
- 拉格朗日定理
- 置换
- 置换群
- 群作用
- 轨道-稳定子定理
- Burnside定理
- 例题 #1 LG-P4980 【模板】Pólya 定理
- Polya定理
- 例题 #2 LG-P4727 [HNOI2009]图的同构计数
- 例题 #3 LG-P4128 [SHOI2006] 有色图
- 例题 #4 UVA10601 Cubes
- 例题 #5 LG-P2561 [AHOI2002]黑白瓷砖
- 例题 #6 SP419 TRANSP - Transposing is Fun
- 例题 #7 SP422 TRANSP2 - Transposing is Even More Fun
- 例题 #8 LG-P4916 [MtOI2018]魔力环
- UPD
更好的阅读体验戳此进入
Tips：不保证正确性，不保证没锅，部分定理可能只是口糊的证明。
群
称集合 $ G $ 和作用于集合 $ G $ 的二元运算 $ \circ $ 为一个群，记作 $ \left(G, \circ \right) $，这里我们简记为 $ \mathbb{G} $，当且仅当其满足以下 $ 4 $ 个性质：
- 封闭性（closure）
若 $ a, b \in \mathbb{G} $，则 $ a \circ b \in \mathbb{G} $。
- 结合律（associativity）
若 $ a, b, c \in \mathbb{G} $，则 $ (a \circ b) \circ c = a \circ (b \circ c) $。
- 单位元（identity element，亦称幺元）
$ \exists e \in \mathbb{G} $ 满足 $ \forall a \in \mathbb{G}, a \circ e = e \circ a = a $，则 $ e $ 称为单位元，其有且仅有一个。
考虑证明，有两个不同的单位元 $ e_1, e_2 $，显然应有 $ e_1 \circ e_2 = e_1 = e_2 \(，则矛盾，\) \texttt{QED} $。
然后根据这个还有个性质：若有 $ a \circ x = a $ 则 $ x = e $。
大概的证明：
- 逆元（inverse element）
$ \forall a \in \mathbb{G} $，总 $ \exists a^{-1} \in \mathbb{G} $，使得 $ a \circ a^{-1} = a^{-1} \circ a = e $，则 $ a^{-1} $ 为 $ a $ 的逆元，有且仅有一个。
考虑证明，首先需要另一个性质，即：$ (a{-1}) = a $，即 $ a $ 的逆元的逆元为 $ a $。
证明：
则有：
然后考虑证明逆元唯一，如果逆元不唯一，我们可以把刚才的性质换一种叙述，任意元素的任意逆元的任意逆元均为元素本身。首先我们可以把群中每个元素作为一个点，逆元的关系当作边，抽象成一个图，由刚才的性质显然应为无向边。如果一个点有多个逆元，那么其应有多条边，且连接的所有其它点度数应仅为 $ 1 $，否则不满足性质，但是此时其连结的点所连结的点（也就是原来的点）的度数不为 $ 1 $ 了，显然矛盾。或者换句话说，这样的图中所有点度数都应为 $ 1 $，这个很好理解，而度数均为 $ 1 $ 即逆元唯一，$ \texttt{QED} $。
e.g. 如整数集和整数间加法构成群 $ \left( \mathbb{Z}, + \right) $，单位元为 $ 0 $，逆元为其相反数。
在实际应用上可以认为树状数组的元素和运算符必须满足群，如 $ \min $ 和 $ \max $ 就因为没有逆元所以不能用树状数组维护。
其它群
半群
称 $ \mathbb{G} $ 是一个半群，当且仅当其满足封闭性与结合律。
幺半群（亚群、含幺子群、独异点）
称 $ \mathbb{G} $ 是一个幺半群，当且仅当其满足封闭性与结合律，且存在单位元。
交换半群
称 $ \mathbb{G} $ 是一个交换半群，当且仅当其满足封闭性与结合律，且其中的运算 $ \circ $ 满足交换律。
交换幺半群（交换亚群）
称 $ \mathbb{G} $ 是一个幺半群，当且仅当其满足封闭性与结合律，且存在单位元，且其中的运算 $ \circ $ 满足交换律。
双半群模型
首先明确一下，该模型一般适用于对于修改与查询的范围有限制的问题中，如：序列区间，树上简单路径，二维平面矩形，高位正交范围，半平面范围，圆范围。
这里的 $ 2^{I_0} $ 表示 $ I_0 $ 的幂集，即 $ I_0 $ 的所有子集构成的集合。
具体来说，给定初始集合 $ I_0 $，一个有限集合 $ I \subset I_0 $，询问集合 $ Q \subset 2^{I_0}, s.t. I_0 \in Q $，交换半群 $ (D, +) $，半群 $ (M, \ast) $，且二元运算符 $ \ast $ 满足 $ D \ast M \rightarrow D $。
满足结合律，且满足 $ \ast $ 对 $ + $ 的分配律，即：$ (a + b) \ast c = a \ast c + b \ast c $。
存在初始权值 $ d_0 : I \to D $。（个人理解的含义是指 $ I $ 中元素的权值在交换半群 $ (D, +) $ 中）
按序执行 $ m $ 个操作，操作为修改或查询，第 $ t $ 个操作定义为：
- 范围修改，给定 $ q_t \in Q, f_t \in M $，定义若 $ x \in q_t $，则 $ d_t(x) = d_{t - 1}(x) \ast f_t $，反之 $ d_t(x) = d_{t - 1}(x) $。
- 范围查询，给定 $ q_t \in Q $，定义 $ d_t(x) = d_{t - 1}(x) $，对所有 $ x \in I $，答案则为 $ \sum_{x \in q_t} d_t(x) $。
所有操作与初始权值均离线给出，用 $ n = \lvert I \rvert $ 表示初始权重的个数，用 $ m $ 表示操作数。
对于满足上述大量限制的模型，我们称为双半群模型。
而为了能够通过线段树等数据结构维护，一般维护的信息都一定需满足半群性质，且大多为交换半群的性质。
而对于一道具体的题目，我们的目的就是去设计 $ D, M $ 而满足上述的双半群模型。
再具体的我也就不会了，总之这似乎是一个很高妙的东西，已知存在的一个可以用的题 LG-P8868 [NOIP2022] 比赛。
阶
定义群的阶为群中元素的数量，记作 $ \lvert \mathbb{G} \rvert $。
子群
若 $ \mathbb{H} \subseteq \mathbb{G} $，且 $ (\mathbb{H}, \circ) $ 构成群，那么称 $ (\mathbb{H}, \circ) $ 为 $ (\mathbb{G}, \circ) $ 的一个子群，简记为 $ \mathbb{H} \le \mathbb{G} $。
陪集
定义与性质
考虑存在 $ \mathbb{H} \le \mathbb{G} $，且有 $ g \in \mathbb{G} $：
我们称 $ { g \circ h \mid h \in \mathbb{H} } $ 为 $ (\mathbb{H}, \circ) $ 在 $ (\mathbb{G}, \circ) $ 内关于 $ g $ 的左陪集，记作 $ g\mathbb{H} $。
同理对于 $ { h \circ g \mid h \in \mathbb{H} } $ 为右陪集，记作 $ \mathbb{H}g $。
对于右陪集，满足以下 $ 6 $ 个性质（左陪集同理）：
- $ \forall g \in \mathbb{G}, \lvert \mathbb{H} \rvert = \lvert \mathbb{H}g \rvert $。
证明：对于 $ \forall h_1, h_2 \in \mathbb{H} $，如果 $ h_1 \circ g = h_2 \circ g $，那么 $ h_1 = h_2 \(，矛盾，\) \texttt{QED} $。
- $ \forall g \in \mathbb{G}, g \in \mathbb{H}g $。
证明：单位元唯一，子集也成群，则子集一定包含该单位元，则有 $ e \circ g \in \mathbb{H}g \Longleftrightarrow g \in \mathbb{H}g \(，\) \texttt{QED} $。
- $ g \in \mathbb{H} \Longleftrightarrow \mathbb{H}g = \mathbb{H} $。
证明：充分性由封闭性易证。必要性：考虑单位元 $ e $，由题意显然有 $ e \circ g = g \in \mathbb{H} \(，\) \texttt{QED} $。
- $ \mathbb{H}a = \mathbb{H}b \Longleftrightarrow a \circ b^{-1} \in \mathbb{H} $。
证明：充分性：$ \mathbb{H}a = \mathbb{H}b \Longleftrightarrow \mathbb{H} a \circ b^{-1} = \mathbb{H} b \circ b^{-1} \Longleftrightarrow \mathbb{H} a \circ b^{-1} = \mathbb{H} \(，由性质3，\) a \circ b^{-1} \in \mathbb{H} \(，\) \texttt{QED} $。必要性反之亦然。
- $ \mathbb{H}a \cap \mathbb{H}b \neq \varnothing \Longleftrightarrow \mathbb{H}a = \mathbb{H}b $。
换句话说，一个子群的陪集的交集要么为空，要么相等。
证明：假设有 $ c \in \mathbb{H}a \land c \in \mathbb{H}b $，且 $ \mathbb{H}a \neq \mathbb{H}b $，则 $ \exists h_1, h_2 \in \mathbb{H}, h_1 \circ a = h_2 \circ b = c $，同 $ \circ $ 一个 $ h_1^{-1} \circ b^{-1} $ 则有 $ a \circ b^{-1} = h_2 \circ h_1^{-1} $，显然 $ h_2 \circ h_1^{-1} \in \mathbb{H} $，则 $ a \circ b^{-1} \in \mathbb{H} $，由性质4可得 $ \mathbb{H}a = \mathbb{H}b \(，矛盾，\) \texttt{QED} $。
- $ \mathbb{H} $ 的所有右陪集的并为 $ G $。
证明：显然 $ e \in \mathbb{H} $，则对于每个关于 $ g $ 的右陪集都含有 $ e \circ g = g $，所有右陪集则包含了 $ \mathbb{G} $ 中的每一个元素，即为 $ G \(，\) \texttt{QED} $。
常见表述
若满足 $ \mathbb{H} \le \mathbb{G} $，则 $ \mathbb{G} / \mathbb{H} $ 表示 $ { g\mathbb{H} \mid g \in \mathbb{G} } $，即 $ \mathbb{G} $ 中所有 $ \mathbb{H} $ 的左陪集。
若满足 $ \mathbb{H} \le \mathbb{G} $，则 $ [\mathbb{G} : \mathbb{H}] $ 表示 $ \mathbb{G} $ 中 $ \mathbb{H} $ 的不同陪集的数量。
拉格朗日定理
对于有限群 $ \mathbb{G} $ 和 $ \mathbb{H} $，若 $ \mathbb{H} \le \mathbb{G} $，则有 $ \lvert \mathbb{H} \rvert \mid \lvert \mathbb{G} \rvert $，也就是 $ \lvert \mathbb{G} \rvert \equiv 0 \bmod{\lvert \mathbb{H} \rvert} $，即 $ \mathbb{H} $ 的阶整除 $ \mathbb{G} $ 的阶。
还有一种表述 $ \lvert \mathbb{H} \rvert \times [\mathbb{G} : \mathbb{H}] = \lvert \mathbb{G} \rvert $。
证明很显然，考虑性质1，5，6易证。
置换
定义
一般用双行表示法表示一个置换，即如：
比较易于理解，即用第二个元素替换第一个元素，第四个替换第二个，以此类推。
特别地，不失一般性，若前者排列为 $ (1, 2, 3, \cdots, n) $，那么不妨直接简记后者排列为置换，即：
所以不难发现，我们可以认为一个序列，或者更严谨的说，一个排列，既可以是一个序列，也可以是一个置换。
同时可以证明，不论表示为双行亦或单行，长度为 $ n $ 的置换个数均为 $ n! $，对于单行表示证明平凡，对于双行可以从定义的角度理解，对于本质相同的双行表示可以认为是同一种单行表示，故置换个数相同。
同时需要注意一点，对于抽象代数中，或者更具体地说，对于群论中，我们认为置换即为集合（通常为有限集）对自身的双射，所以置换应该认为是严格的排列，而组合数学中只要求无重复，但却是可以有阙漏的。但当然本文中的置换均指严格的双射。
运算
对于置换 $ \sigma $ 和序列 $ a $ 的运算，一般记作 $ \sigma \times a $ 或 $ \sigma(a) $，即 $ \sigma(a) = (a_{\sigma_1}, a_{\sigma_2}, \cdots, a_{\sigma_n}) $。一般称此过程为置换的合成。
当然更严谨地说，实际上应该是对于置换 $ \sigma $ 和置换 $ a $ 之间的运算，上文记作序列仅为更好理解。
具体来说，个人理解该合成运算是可以定义在置换和序列之间的，也就是对于如 $ a = (1, 1, 1, 1, 1) $，这是序列，但不是置换，但也可以与置换进行右乘（不是乘法）操作而生成新的序列，这里在群作用处会用到更多一些。
置换群
定义
称对于集合 $ N = {1, 2, \cdots, n} $ 的若干个排列构成的集合 $ M $，或者更严格地说，应该是这些排列代表的置换，以及置换之间的 “合成” 操作的二元运算符，即上文的 $ \times $ 所构成的群 $ (M, \times) $ 为置换群。
简而言之，置换群即为若干置换和置换之间的合成运算构成的群。
显然置换群存在单位元 $ e = (1, 2, \cdots, n) \(，证明：\) a \times e = e \times a = a \(，\) \texttt{QED} $。
同时显然 $ \times $ 运算满足结合律，证明可以通过将置换抽象成有向边理解，较为显然。
群作用
群对自身的作用
对于群 $ \mathbb{G} $，及 $ \forall g \in \mathbb{G} $，用 $ g $ 左乘 $ \mathbb{G} $ 的所有元素（包括 $ g $），可以看成一种 $ \mathbb{G} $ 到自身的映射：$ f_g: \mathbb{G} \rightarrow \mathbb{G} $，使得对于 $ \forall g \in \mathbb{G} $，有 $ f_g(x) = g \times x $。
如此对于群中每个元素都能形成一个这样的映射，此时我们可以考虑将所有的映射放到一起，定义为一个二元的映射，即 $ f: \mathbb{G} \times \mathbb{G} \rightarrow \mathbb{G} $。也就是说对于 $ \forall g, x \in \mathbb{G} $，有 $ f(g, x) = f_g(x) = g \times x $，对于这样的一个映射即称其为群作用。
然后这个东西一般我们称其为左平移作用，同理也存在右平移作用，这里不再赘述。
群作用
更一般地，对于对于群 $ \mathbb{G} $ 和集合 $ M $，群中每个元素都能代表一个 $ M \rightarrow M $ 的映射，记映射 $ f: \mathbb{G} \times M \rightarrow M $，若该映射满足以下两条公理：
结合律：对于 $ g_1, g_2 \in \mathbb{G}, m \in M $，有 $ f(g_1, f(g_2, m)) = f(g_1 \times g_2, m) $。
单位元恒等映射：对于 $ \mathbb{G} $ 的单位元 $ e $，有 $ f(e, m) = m $。
则称群 $ \mathbb{G} $ 作用于集合 $ M $ 上。
不难想到该映射应为双射，考虑证明：对于 $ \forall m \in M, \forall g \in \mathbb{G} $，存在 $ f(g^{-1}, f(g, m)) = m $，而逆元唯一，若两个不同的 $ m $ 通过同一置换 $ g $ 指向了相同的 $ m' $，但 $ m' $ 通过唯一的 $ g^{-1} $ 应仅能指向唯一的 $ m'' \(，矛盾，\) \texttt{QED} $。
但是注意，不同的 $ m $ 不可能通过相同的 $ g $ 得到相同的 $ m' $，但相同的 $ m $ 可能通过不同的 $ g $ 得到相同的 $ m' $。举个例子如 $ m = (1, 1, 1, 1, 1) $，对于任意的 $ g $ 都可以使得 $ m \rightarrow m $。
轨道-稳定子定理
轨道
对于作用在集合 $ X $ 上的群 $ \mathbb{G} \(。\) X $ 中的一个元素 $ x $ 的轨道即为 $ x $ 通过 $ \mathbb{G} $ 中的元素个可以置换到的元素的集合。记 $ x $ 的轨道为 $ \mathbb{G}(x) $。
稳定子
记 $ g(x) $ 为 $ f(g, x) $，则稳定子为 $ \mathbb{G}^x = {g \mid g \in \mathbb{G}, g(x) = x} $。
简而言之就是群中所有满足 $ g(x) = x $ 的 $ g $ 构成的集合。
轨道-稳定子定理
抽象一点地表述，轨道-稳定子定理即为：
即元素 $ x $ 稳定子大小和轨道的大小的乘积即为群的阶（或者说群的大小）。
证明
首先 $ \mathbb{G}^x \le \mathbb{G} $，且 $ e \in \mathbb{G}^x $，证明显然。
满足结合律，封闭性，以及存在逆元易证，这里不再赘述。
我们可以先考虑一个固定的 $ x $ 以其 $ \forall g \in \mathbb{G} $，考虑将 $ g $ 标号，不难想到一定存在如下映射关系：
显然可能存在 $ n = 1 $，这里记作这样仅为方便举例。当然也可以将上式记作 $ g_1(x) = g_2(x) = \cdots = g_n(x) = x_1, \cdots $。同时这里为什么每一段的长度都是相同的，或者说满足 $ x \rightarrow x_i $ 的 $ g $ 个数相同，我们会在后文提到。
此处我们记 $ g $ 表示固定的任意一个稳定子，记 $ g' $ 为固定的任意一个 $ \mathbb{G} $ 中非稳定子的元素，记 $ g_1 $ 为固定的满足 $ x \rightarrow x_1 $ 的任意一个映射。
换句话说，满足 $ g(x) = x, g'(x) \neq x, g_1(x) = x_1 $。
显然 $ g_1(g(x)) = g_1(x) = x_1 $，而对于 $ g_1(g'(x)) $，因 $ g'(x) \neq x $，所以 $ g_1(g'(x)) \neq x_1 $，这个通过我们在群作用处证明的对于固定的 $ g $ 可变的 $ m \(，\) f(g, m) $ 是双射可显然证明。
此时我们将刚才的结论换种表述方式，即对于 $ g_1(x) = x_1 \(，\) g_1(g(x)) = x_1 $ 当且仅当 $ g(x) = x $。当然由结合律也可以写成 $ g_1 \circ g $ 的形式。所以再换一种方式说的话，就是有且仅有稳定子对 $ g_1 $ 作用之后仍然满足 $ g_1(x) = x_1 $。
同理此结论推导至 $ g_2, g_3, \cdots $ 均成立。
现在我们再继续推导，仍令 $ g_1 $ 满足 $ g_1(x) = x_1 $，并固定 $ g_1 $，此时再令 $ \forall g'' \in \mathbb{G} $，发现如果我们做 $ \mathbb{G} $ 在 $ \mathbb{G} $ 关于 $ g_1 $ 的陪集，其可记作：$ g_1\mathbb{G} = { g_1 \circ g'' \mid g'' \in \mathbb{G} } = \mathbb{G} $，至于最后一步转换为 $ \mathbb{G} $，由陪集性质 $ 3 $ 可得 $ g\mathbb{G} = \mathbb{G} $。也就是说 $ g_1 $ 对任意 $ g'' $ 运算之后结果构成的集合就是原群 $ \mathbb{G} $。
现在我们再把目光放回证明的前半部分，只有稳定子能够使得 $ g_1(x) = x_1 $，那么我们考虑所有的 $ g_1 \circ g'' $，当且仅当 $ g'' \in \mathbb{G}^x $，那么映射不变，而这样的话，不难发现在我们前面记录映射时用的 $ n $，其实满足 $ n = \lvert \mathbb{G}^x \rvert $。当然这里可能会有点小问题，我们刚才已经固定了 $ g_1 $，那么对于 $ g_2 $ 等难道不会对证明造成影响吗？显然不会。从我们之前的证明内容不难发现，我们这里找的稳定子 $ g'' $ 实际上是根据 $ x \rightarrow x_1 $ 找的，与 $ g_1 $ 只是表面上的关系，所以对于 $ g_1, g_2, \cdots g_n $，他们对应的 $ g'' $ 实际上是完全相同的。所以既然满足 $ n = \lvert \mathbb{G}^x \rvert $，而 $ x_1, x_2, \cdots $ 共有轨道数个，即 $ \lvert \mathbb{G}(x) \rvert $ 个，每个长度又相等，自然乘起来就是整个群的阶了，即 $ \lvert \mathbb{G}^x \rvert \times \lvert \mathbb{G}(x) \rvert = \lvert \mathbb{G} \rvert \(，\) \texttt{QED} $。
Tips：这里我们可以在回过头考虑为什么每一段 $ x \rightarrow x_i $ 的 $ g $ 数量相同，从上一段文字则不难理解，能够使 $ g_1(g''(x)) = x_1 $ 的 $ g'' $，共有 $ \lvert \mathbb{G}^x \rvert $ 个，对于同一对应关系的不同映射之间的 $ g'' $ 也是等效的，那么这一段的 $ n $ 显然就是 $ \lvert \mathbb{G}^x \rvert $，所以说每一段长度一定相同且均为 $ \lvert \mathbb{G}^x \rvert $。
证明2
除了上面的方法之外，仍存在一个思路：
根据拉格朗日定理可知 $ \lvert \mathbb{G}^x \rvert \times [\mathbb{G} : \mathbb{G}^x] = \lvert \mathbb{G} \rvert $。
于是问题转化为需要证明 $ \lvert \mathbb{G}(x) \rvert = [\mathbb{G} : \mathbb{G}^x] $。
也就是说稳定子的关于原群的不同陪集数量等于轨道的大小。
可以再次转化为证明每一个 $ g(x) $，或者说对于固定的 $ x $ 的每一个 $ g(x) $，都对应一个陪集。
然后这个地方的证明较为复杂，就不再赘述了。
Burnside定理
不动点
类似于稳定子，对于稳定子中 $ g(x) = x \(，\) g $ 为稳定子，$ x $ 为不动点。
对于集合 $ X $，记 $ X^g $ 表示集合 $ X $ 在 $ g $ 的作用下的不动点的集合。
等价类
对于置换群 $ \mathbb{G} $，定义其作用于集合 $ X $，若对于 $ x, y \in X \(，\) \exists g \in \mathbb{G} $，使得 $ g(x) = y $，那么 $ x, y $ 在同一个等价类中。
定理
同等价类的定义中，不同的等价类的数量，记作 $ \lvert X / \mathbb{G} \rvert $，为：
也就是说等价类的数量等于每一个 $ g $ 作用于 $ X $ 的不动点的数量的算术平均值。
证明
首先考虑把不动点转化为稳定子，较为显然：
然后用轨道-稳定子定理转化一下，即：
然后把分子提出来，再将枚举 $ X $ 的元素转化为枚举 $ X $ 的每个等价类里的每个元素：
显然一个等价类的轨道的大小就是等价类的大小，所以此时 $ \lvert \mathbb{G}(x) \rvert = \lvert Y \rvert $。
不难发现有：$ \sum_{x \in Y} \dfrac{1}{\lvert Y \rvert} = 1 $。
所以最终转化为：
也就是等价类的个数了，所以最终式子化为：
然后把这个带入原定理的 $ \texttt{RHS} $ 即得证。
Tips
对于这个东西有一个例子，十分形象：
例题 #1 LG-P4980 【模板】Pólya 定理
题面
求 $ n $ 个点 $ n $ 条边的环用 $ n $ 种颜色给点染色，有多少种本质不同染色方案。答案对 $ 1e9 + 7 $ 取模。
Solution
原题的问题可以转化为：
在置换群 $ \mathbb{G} = { \texttt{旋转0个}, \texttt{旋转1个}, \texttt{旋转2个}, \cdots, \texttt{旋转n-1个} } $，作用于 $ n^n $ 种染色方案的集合 $ M $ 得到的等价类的数量。
根据 Burnside定理 可知答案即为：
然后考虑一下这个枚举的过程。
显然对于旋转 $ 0 $ 的整个 $ M $ 均为不动点，所以答案的贡献为 $ n^n $。
对于旋转 $ k $ 的，如果一个点是不动点，那么其应该是以 $ a $ 为循环节，且 $ a \mid k $，并且同时亦必须有 $ a \mid n $，所以即为 $ a \mid \gcd(n, k) $，那么也就可以认为只需要满足为任意的长度为 $ \gcd(n, k) $ 的染色方案的循环的染色方案即可。
故最终答案可以转化为：
然后不难发现这东西就是个标准莫反，考虑枚举 $ \gcd $。
然后右边的显然是 $ \varphi(\dfrac{n}{d}) $。
所以最终式子为：
然后大概分析一下这个的复杂度，枚举因数是 $ O(\sqrt{n}) $ 的，快速幂是 $ O(\log n) $ 的，求欧拉函数可以通过 $ O(\sqrt{n}) $ 分解质因数之后直接枚举求得，最后复杂度似乎是 $ O(T\sqrt{n}\log n) $ 的，看起来完全不能通过，但是因为卡不满，这样就可以过这道题了。
然后似乎直接强行枚举 $ n $ 的因数，然后再直接强行求 $ \varphi $，这样大概是 $ O(T(\sqrt{n}\log n + n^{\tfrac{3}{4}})) $，还是看起来不能过，但是可以过。
当然，因为本题题目名就是 Polya定理 模板，那么我们可以再考虑一下 Polya 的推导方式。
Code
#define _USE_MATH_DEFINES
#include <bits/stdc++.h>
#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW(arr) void* Edge::operator new(size_t){static Edge* P = arr; return P++;}
using namespace std;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;
#define MOD (ll)(1e9 + 7)
template < typename T = int >
inline T read(void);
bitset < 110000 > notPrime;
basic_string < ll > Prime;
void Init(void){
for(ll i = 2; i <= 101000; ++i){
if(!notPrime[i])Prime += i;
for(auto p : Prime){
if(p * i > 101000)break;
notPrime[p * i] = true;
if(i % p == 0)break;
}
}
}
ll qpow(ll a, ll b){
ll ret(1), mul(a);
while(b){
if(b & 1)ret = ret * mul % MOD;
b >>= 1;
mul = mul * mul % MOD;
}return ret;
}
ll phi(ll x){
ll ret(x);
basic_string < ll > fact;
for(auto p : Prime){
if(p * p > x)break;
if(x % p == 0)fact += p;
while(x % p == 0)x /= p;
}if(x != 1)fact += x;
for(auto p : fact)ret /= p, ret *= (p - 1);
return ret;
}
int main(){
Init();
int T = read();
while(T--){
ll N = read < ll >();
ll ans(0);
for(ll i = 1; i * i <= N; ++i){
if(N % i != 0)continue;
(ans += qpow(N, i) * phi(N / i) % MOD) %= MOD;
if(i * i != N)(ans += qpow(N, N / i) * phi(i) % MOD) %= MOD;
}(ans *= qpow(N, MOD - 2)) %= MOD;
printf("%lld\n", ans);
}
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
template < typename T >
inline T read(void){
T ret(0);
int flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
Polya定理
这里我们基于刚才的模板题来叙述 Polya定理。
这个东西我认为也可以看作是 Burnside定理 的推论。
考虑一个置换，用 $ (a_1, a_2, \cdots, a_n) $ 单行表示。然后我们在一般 Burnside 的时候求的是不动点的数量，于是我们考虑发现若对于这样一个置换，我们令每个 $ i $ 向 $ a_i $ 连边，不难发现得到的就是若干个环，同时不难想到，我们若要使其为不动点，那么环上所有点的颜色都应相同。
令环的数量为 $ c(g) $ 为置换 $ g $ 能够形成的环数，于是 Burnside定理 的式子就可以转化为：
也就是每个环任意选择一个颜色。
然后推导是类似的，对于旋转 $ 0 $ 个与上文相同，对于旋转 $ k $ 个的 $ g $，显然 $ c(g) = \gcd(n, k) $。然后式子就和刚才用 Burnside 所推导的完全相同了。
例题 #2 LG-P4727 [HNOI2009]图的同构计数
题面
一道 NP 问题，求互不同构的含 $ n $ 个点的图有多少种。
Solution
首先称两个图同构，当且仅当两个图可以通过对顶点的重标号使得两图完全相同。
然后这个东西的答案是一个数列，OEIS 上的编号是 A000088。
然后我们再次回到 Burnside定理，集合 $ X $ 即为 $ n $ 个顶点可能构成的 $ 2^{n \choose 2} = 2^\tfrac{n(n - 1)}{2} $ 个简单无向图。置换群 $ \mathbb{G} $ 即为 $ [1, n] $ 的全排列。
然后我们的难点依然在于求不动点的数量。也就是说对于一个置换 $ g $，有多少图在经过置换 $ g $ 之后与原图同构。
下面将会有一个与上一题，即 Polya定理 模板，或者说群论的标准套路。我们可以考虑先将图认为是完全图，然后用两种颜色对边进行染色，两种颜色表示该边存在或不存在。于是此时我们就会发现对于某一个置换 $ g $，仍然存在一个等价类中，所有边必须均存在或不存在。
举个例子，对于一个标号为 $ 1, 2, 3 $ 的三角形完全图，如果有置换 $ g = (2, 3, 1) $，那么此时不难发现三条边同属一个等价类，因为你要么使三条边均存在，要么均不存在，否则按照这个置换的意义，旋转一下三角形，就会使得图不同构。此时的 $ g $ 对应的不动点即为 $ 2^1 = 2 $ 个。
所以说上面我们说的这一对，就是标准的 Polya定理，即 $ \lvert X^g \rvert = 2^{c(g)} $。
所以现在关键就在于我们如何求这个 $ c(g) $。
首先我们会发现，对于一个置换 $ g $，其是可以被分成多个不相交的部分的，用双行表示法举个例子：
考虑若将置换 $ g $ 拆成 $ k $ 个循环，长度分别为 $ b_1, b_2, \cdots, b_k $。然后不难发现有两种边：
首先考虑对于两个点均在同一段循环内的边：
然后我们考虑对于一种置换中的一个长度为 $ b $ 的循环，有一个结论，这样的循环共有 $ \lfloor \dfrac{b}{2} \rfloor $ 个等价类。
我们可以将对应的点数排成一个正 $ n $ 边形，比如 $ n = 6 $ 的时候，如果有这样一个置换 $ g = \begin{pmatrix}
1 & 2 & 3 & 4 & 5 & 6 \
2 & 3 & 4 & 5 & 6 & 1
\end{pmatrix} $，存在这样的图和边：
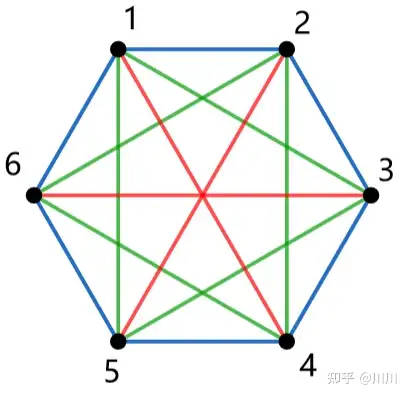
不难发现对于长度相同的边都是等价的，其必须同时染或不染，否则置换后将会不同构。而不难想到，由于正 $ b $ 边形存在对称性，所以线段的长度共有 $ \lfloor \dfrac{b}{2} \rfloor $ 种，所以等价类也就共有这些种。
于是其贡献的等价类数量为：$ \sum_{i = 1}^k \lfloor \dfrac{b_i}{2} \rfloor $。
然后考虑在不同循环中的边：
举个例子：
这个东西的图大概是这样的：
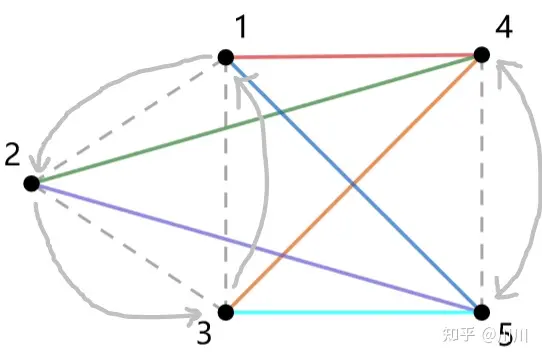
如对于长度为 $ b_1, b_2 $ 的两个循环，那么两者之间共有 $ b_1 \times b_2 $ 条边，所以在这两者之间的边，每次经过 $ \operatorname{lcm}(b_1, b_2) $ 次置换之后就会回到原位，则等价类的大小，或者说环长为 $ \operatorname{lcm}(b_1, b_2) $，那么此时等价类个数，也就是环种类数，即为 $ \dfrac{b_1 \times b_2}{\operatorname{lcm}(b_1, b_2)} $，也就是 $ \gcd(b_1, b_2) $。
所以这些边的贡献的等价类个数即为：
所以最终等价类的个数即为：
答案即为：
不过 $ \mathbb{G} $ 是 $ n! $ 的，复杂度肯定不行，尝试优化；
考虑发现很多置换会被重复计算，如：
这样的 $ b_k $ 都是 $ 1, 2, 3 $，那么 $ c(g) $ 的值是相同的。
也就是说对于相同的 $ n $ 的拆分贡献是相同的，所以可以考虑枚举 $ n $ 的拆分。
考虑对于一种拆分，计算有多少种对应的置换，首先总共有 $ n! $，但是对于每一段长度为 $ b $ 的循环，都需要使其从普通排列转换为圆排列，也就是先去掉重复的 $ b! $，然后再乘上圆排列的 $ (b - 1)! $，并且对于相同长度的多个循环，假设有 $ c $ 个，那么这里又会重复 $ c! $ 个，那么在去重后应该为：
然后这里再枚举每个 $ n $ 的拆分，答案即为：
然后化简一下即为：
这样便可以通过了。然后尝试分析一下复杂度：
枚举 $ n $ 的拆分是 A000041，然后对于拆分长度为 $ k $ 的求解为 $ O(k^2) $ 的，最终应为 A296010，然后这个东西完全不知道怎么分析，总之最后的复杂度大约在 $ O(10^{\sqrt{n}}) $，虽然我也不知道是怎么分析出来的。。。
Code
#define _USE_MATH_DEFINES
#include <bits/stdc++.h>
#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW(arr) void* Edge::operator new(size_t){static Edge* P = arr; return P++;}
using namespace std;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;
#define MOD (997)
template < typename T = int >
inline T read(void);
int N;
ll fact[110], inv[110], inv_d[110];
int cnt[110];
ll ans(0);
basic_string < int > cur;
unordered_set < int > exist;
ll qpow(ll a, ll b){
ll ret(1), mul(a);
while(b){
if(b & 1)ret = ret * mul % MOD;
b >>= 1;
mul = mul * mul % MOD;
}return ret;
}
void Init(void){
for(int i = 1; i <= 100; ++i)inv_d[i] = qpow(i, MOD - 2);
fact[0] = 1;
for(int i = 1; i <= 100; ++i)fact[i] = fact[i - 1] * i % MOD;
inv[100] = qpow(fact[100], MOD - 2);
for(int i = 99; i >= 0; --i)inv[i] = inv[i + 1] * (i + 1) % MOD;
}
void dfs(int lft = N){
if(!lft){
ll C(0);
for(auto i : cur)C += i >> 1;
for(int i = 1; i <= (int)cur.size(); ++i)
for(int j = 1; j <= i - 1; ++j)
C += __gcd(cur.at(i - 1), cur.at(j - 1));
ll ret = qpow(2, C);
for(auto i : cur)(ret *= inv_d[i]) %= MOD;
for(auto i : exist)(ret *= inv[cnt[i]]) %= MOD;
(ans += ret) %= MOD;
return;
}
for(int i = cur.empty() ? 1 : cur.back(); i <= lft; ++i){
cur += i, ++cnt[i], exist.insert(i);
dfs(lft - i);
cur.pop_back();
if(!--cnt[i])exist.erase(i);
}
}
int main(){
Init();
N = read();
dfs();
printf("%lld\n", ans);
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
template < typename T >
inline T read(void){
T ret(0);
int flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
例题 #3 LG-P4128 [SHOI2006] 有色图
双倍经验，将 $ 2^{c(g)} $ 改为 $ m^{c(g)} $ 即可。
例题 #4 UVA10601 Cubes
题面
给定 $ 12 $ 根木棍的颜色，颜色最多 $ 6 $ 种，求其能构成的本质不同正方体的数量。
Solution
依然尝试考虑 Burnside定理，即：
集合 $ X $ 即为 $ 12 $ 根木棒构成的正方体，然后置换群 $ \mathbb{G} $ 则要复杂一些，其中元素即为对于正方体的各种旋转等操作，同时不难发现，对于任意一种旋转，会存在多个循环，或者说多个环，而在同一个环中所有边的颜色应该是相同的，否则其必定不可能为不动点。考虑分类讨论：
结论：对于正方体的旋转共有 $ 24 $ 种。
对于恒等变换，共 $ 1 $ 种，环长为 $ 1 $。
对于沿对面中心定向旋转 $ 90^\circ $ 和 $ 270^\circ $，共 $ 3 \times 2 = 6 $ 种，环长为 $ 4 $。
对于沿对面中心旋转 $ 180^\circ $，共 $ 3 $ 种，环长为 $ 2 $。
对于沿对棱中点旋转 $ 180^\circ $，有 $ 6 $ 对对棱，共 $ 6 $ 种，环分为两种，存在 $ 2 $ 个环长为 $ 1 $ 的环和 $ 5 $ 个环长为 $ 2 $ 的环。
对于沿相对顶点定向旋转 $ 120^\circ $ 和 $ 240^\circ $，相对顶点共有 $ 4 $ 对，则共 $ 4 \times 2 = 8 $ 种，环长为 $ 3 $。
故置换的个数共 $ 1 + 6 + 3 + 6 + 8 = 24 $ 种。
如果直接枚举所有排列然后计算不动点再去重似乎有点卡，感觉复杂度似乎是 $ O(24 \times 12!) $，好像过不了。
考虑将构建长方体转换为进行圆排列，不难发现大多数的置换的环长都是相同的，令环长为 $ x $，则可以将问题转换为有 $ 6 $ 种颜色，每种颜色有 $ c_i $ 个，然后 $ \sum c_i = 12 $，用其进行圆排列。然后考虑一下环长再次转换，即颜色有 $ \dfrac{c_i}{x} $ 个，共有 $ \dfrac{12}{x} $ 个环，对环进行染色，这样的话就又变成普通排列了，于是问题转化为多重集排列，从所有排列中去重即可，最终答案：
对于不满足 $ x \mid c_i $ 的直接忽略即可。
然后对于两种环的部分，枚举两个环长为 $ 1 $ 的环是什么颜色即可，然后去掉这两个后对剩下的按照相同方式计算即可。
最后复杂度总之是 $ O(\texttt{能过}) $。
Code
#define _USE_MATH_DEFINES
#include <bits/stdc++.h>
#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW(arr) void* Edge::operator new(size_t){static Edge* P = arr; return P++;}
using namespace std;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;
template < typename T = int >
inline T read(void);
int cnt[7];
ll fact[13];
void Init(void){
fact[0] = 1;
for(int i = 1; i <= 12; ++i)fact[i] = fact[i - 1] * i;
}
ll Cal(int len, int siz = 12){
if(siz % len)return 0;
ll ret = fact[siz / len];
for(int i = 1; i <= 6; ++i){
if(cnt[i] % len)return 0;
else ret /= fact[cnt[i] / len];
}return ret;
}
int main(){
Init();
int T = read();
while(T--){
memset(cnt, 0, sizeof cnt);
for(int i = 1; i <= 12; ++i)cnt[read()]++;
ll ans(0);
ans += Cal(1) + 6 * Cal(4) + 3 * Cal(2) + 8 * Cal(3);
for(int i = 1; i <= 6; ++i){
if(!cnt[i])continue;
--cnt[i];
for(int j = 1; j <= 6; ++j){
if(!cnt[j])continue;
--cnt[j];
ans += Cal(2, 10) * 6;
++cnt[j];
}++cnt[i];
}printf("%lld\n", ans / 24);
}
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
template < typename T >
inline T read(void){
T ret(0);
int flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
例题 #5 LG-P2561 [AHOI2002]黑白瓷砖
题面
有点繁琐，挂两个图片吧。
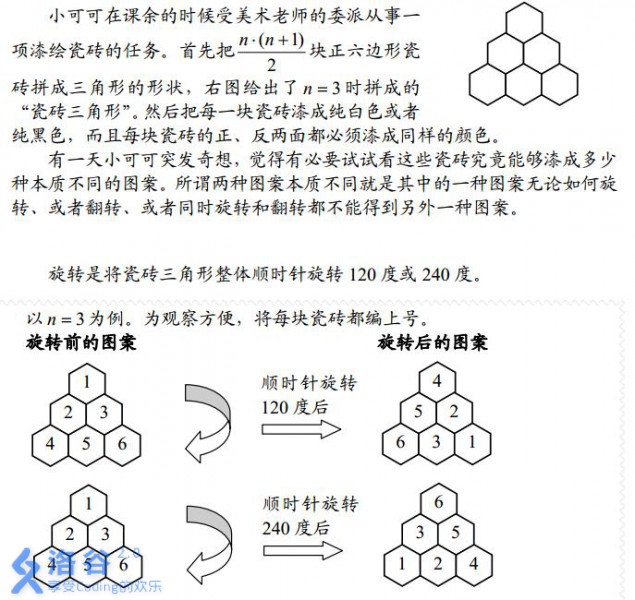
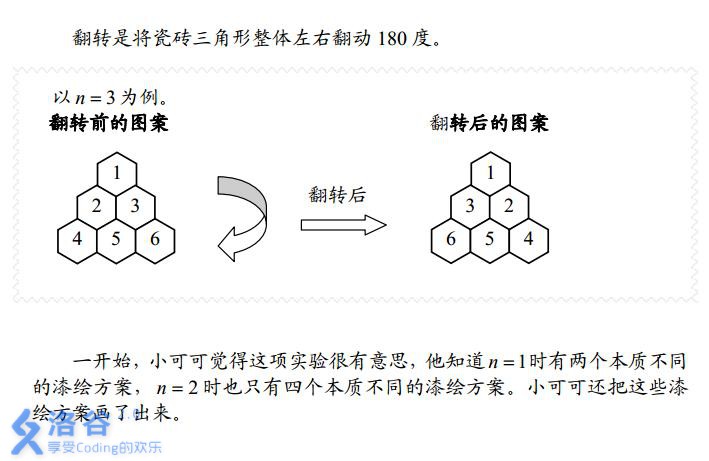
Solution
显然置换群为：
分别考虑，对于旋转，考虑 Polya定理，每个环长均为 $ 3 $，且可能存在环长为 $ 1 $ 的一个中心点，所以贡献为：
对于翻转，要求对称，环长为 $ 1 $ 或 $ 2 $，不难发现贡献为：
对于静止，贡献为：
套用一下 Polya定理 即可。
注意需要高精度。
Code
#define _USE_MATH_DEFINES
#include <bits/stdc++.h>
#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW void* Edge::operator new(size_t){static Edge* P = ed; return P++;}
#define ROPNEW_NODE void* Node::operator new(size_t){static Node* P = nd; return P++;}
using namespace std;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;
template < typename T = int >
inline T read(void);
int N;
class Bignum{
private:
public:
basic_string < int > nums;
friend Bignum operator + (Bignum a, Bignum b){
reverse(a.nums.begin(), a.nums.end());
reverse(b.nums.begin(), b.nums.end());
while(a.nums.size() < b.nums.size())a.nums += 0;
while(b.nums.size() < a.nums.size())b.nums += 0;
Bignum ret; bool plus(false);
for(int i = 0; i < (int)a.nums.size(); ++i){
a.nums.at(i) += b.nums.at(i) + plus;
plus = false;
if(a.nums.at(i) >= 10)
plus = true, a.nums.at(i) %= 10;
}
if(plus)a.nums += 1;
reverse(a.nums.begin(), a.nums.end());
return a;
}
friend Bignum operator * (Bignum a, Bignum b){
reverse(a.nums.begin(), a.nums.end());
reverse(b.nums.begin(), b.nums.end());
Bignum ret;
for(int i = 1; i <= (int)(a.nums.size() + b.nums.size()); ++i)ret.nums += 0;
for(auto i = 0; i < (int)a.nums.size(); ++i)
for(int j = 0; j < (int)b.nums.size(); ++j)
ret.nums.at(i + j) += a.nums.at(i) * b.nums.at(j);
for(int i = 0; i < (int)ret.nums.size() - 1; ++i)
ret.nums.at(i + 1) += ret.nums.at(i) / 10, ret.nums.at(i) %= 10;
if(ret.nums.back() >= 10)ret.nums += ret.nums.back() / 10, *prev(ret.nums.end(), 2) %= 10;
while(ret.nums.size() > 1 && ret.nums.back() == 0)ret.nums.pop_back();
reverse(ret.nums.begin(), ret.nums.end());
return ret;
}
friend Bignum operator / (Bignum a, ll div){
Bignum ret;
ll cur(0); bool flag(false);
for(auto i : a.nums){
cur *= 10, cur += i;
if(cur < div && !flag)continue;
flag = true, ret.nums += cur / div, cur %= div;
}return ret;
}
void Print(void){
for(auto v : nums)printf("%d", v);
printf("\n");
}
};
Bignum qpow(Bignum a, ll b){
Bignum ret, mul(a);
ret.nums += 1;
while(b){
if(b & 1)ret = ret * mul;
b >>= 1;
mul = mul * mul;
}return ret;
}
int main(){
N = read();
Bignum ans; ans.nums += 0;
Bignum base; base.nums += 2;
ans = ans + (qpow(base, (ll)ceil((ld)N * (N + 1) / 6.0)) * base);
ll num(0);
for(int i = 1; i <= N; ++i)num += (i + 1) >> 1;
Bignum mul; mul.nums += 3;
ans = ans + (qpow(base, num) * mul);
ans = ans + qpow(base, (N * (N + 1)) >> 1);
ans = ans / 6ll;
ans.Print();
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
template < typename T >
inline T read(void){
T ret(0);
int flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
例题 #6 SP419 TRANSP - Transposing is Fun
题面
给定 $ a, b $，存在 $ 2^a \times 2^b $ 的任意矩阵，现在求其转置矩阵，但仅能用交换两个元素的操作，求最少的操作次数能够求得任意该大小矩阵的转置矩阵。特别地，我们将矩阵抽象成序列，具体地，按照第一行的元素、第二行的元素、第三行的元素……存储。
Solution
一道很好的群论题，尤其是其中转化的思想还是很高妙的。
不难发现，我们考虑按序为矩阵标号，从 $ 0 $ 开始，则问题转化为我们要进行一次类似于置换的操作，如对于 $ a = 1, b = 2 $：
这个东西朴素的交换次数是 $ 2^{a + b} $ 的，但是不难发现，对于一个循环的置换，我们是可以优化掉一次交换操作的，如 $ (1, 2, 4) \rightarrow (4, 1, 2) $ 就可以用 $ 3 - 1 = 2 $ 次解决，于是如果我们找出整体有多少个循环，令其为 $ x $，则答案为 $ 2^{a + b} - x $，考虑计算 $ x $。
由题面中 $ 2^a $ 的信息我们或许可能想到将其从二进制上考虑，发现变化即为将其二进制循环向右位移 $ a $ 位，或向左平移 $ b $ 位，证明不难，考虑转置变化为：$ i \times 2^b + j \rightarrow j \times 2^b + i $，意义上就是将二进制位分割后交换，与上述操作等效。
于是我们想到，若将二进制数抽象为长度为 $ a + b $ 的环，对其进行 $ 0/1 $ 染色，置换为静止和旋转 $ a $，对于旋转 $ a $，显然环数为 $ \gcd(a, a + b) = \gcd(a, b) $，看起来很正确，但是仔细想一下就会发现这个置换群不存在逆元，所以不是群，无法计算。
这时就存在一个很人类智慧的转化，我们可以容易想到每 $ \dfrac{a + b}{\gcd(a, b)} $ 个点在一个环内，或者说每 $ \gcd(a, b) $ 个数之后就会遇到应与其在同一环内的点，那么我们就可以将这 $ \gcd(a, b) $ 个点缩为一个大点这样它们之间的任意染色都不会使得数同构，那么问题转化为我们用 $ 2^{\gcd(a, b)} $ 个颜色去染 $ \dfrac{a + b}{\gcd(a, b)} $ 个点，令 $ n = \dfrac{a + b}{\gcd(a, b)} $ 置换为旋转 $ 0, 1, 2, \cdots, n - 1 $。现在其满足性质，直接套用 Polya定理，考虑经典套路，得到：
用经典的莫反思想推导：
可以通过精细实现达到 $ O(T(\sqrt{n} + \log n)) $ 的复杂度，但是意义不大，本题不卡，直接 $ O(T(n^{\tfrac{3}{4}} + \sqrt{n} \log n)) $ 强行处理即可。
Code
#define _USE_MATH_DEFINES
#include <bits/stdc++.h>
#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW void* Edge::operator new(size_t){static Edge* P = ed; return P++;}
#define ROPNEW_NODE void* Node::operator new(size_t){static Node* P = nd; return P++;}
using namespace std;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;
#define MOD (1000003ll)
#define LIMIT (510000)
template < typename T = int >
inline T read(void);
int A, B;
int N;
basic_string < int > Prime;
bitset < LIMIT + 100 > notPrime;
ll qpow(ll a, ll b){
ll ret(1), mul(a);
while(b){
if(b & 1)ret = ret * mul % MOD;
b >>= 1;
mul = mul * mul % MOD;
}return ret;
}
int Phi(int x){
int ret(x);
basic_string < int > fact;
for(auto p : Prime){
if(p * p > x)break;
if(x % p == 0)fact += p;
while(x % p == 0)x /= p;
}if(x != 1)fact += x;
for(auto f : fact)ret /= f, ret *= (f - 1);
return ret;
}
int main(){
for(int i = 2; i <= LIMIT; ++i){
if(!notPrime[i])Prime += i;
for(auto p : Prime){
if(p * i > LIMIT)break;
notPrime[p * i] = true;
if(i % p == 0)break;
}
}
int T = read();
while(T--){
A = read(), B = read();
N = (A + B) / __gcd(A, B);
ll ans(0);
for(int i = 1; i * i <= N; ++i){
if(N % i)continue;
if(i * i != N)
(ans += qpow(2, (ll)__gcd(A, B) * i) * Phi(N / i) % MOD) %= MOD,
(ans += qpow(2, (ll)__gcd(A, B) * (N / i)) * Phi(i) % MOD);
else (ans += qpow(2, (ll)__gcd(A, B) * i) * Phi(N / i) % MOD) %= MOD;
}(ans *= qpow(N, MOD - 2)) %= MOD;
printf("%lld\n", (qpow(2, A + B) - ans + MOD) % MOD);
}
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
template < typename T >
inline T read(void){
T ret(0);
int flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
例题 #7 SP422 TRANSP2 - Transposing is Even More Fun
题面
与 SP419 TRANSP - Transposing is Fun 相同，仅略增大数据范围。
Solution
有点不太理解这道题的意义，完全就是更卡常一点，需要更加精细实现，本质没有任何变化。。
推导部分完全相同，最终式子：
发现对于 $ 2^k $ 最多 $ \dfrac{a + b}{\gcd(a, b)} \times \gcd(a, b) = a + b $，于是可以预处理 $ 2^k $，然后我们可以通过分解质因数后 dfs 跑一下，同时处理 $ \varphi $ 即可每次 $ O(\sqrt{n}) $ 处理该式，故最终复杂度 $ O((a + b) + T(\sqrt{n} + \log n)) $，可以通过。
Code
#define _USE_MATH_DEFINES
#include <bits/stdc++.h>
#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW void* Edge::operator new(size_t){static Edge* P = ed; return P++;}
#define ROPNEW_NODE void* Node::operator new(size_t){static Node* P = nd; return P++;}
using namespace std;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;
#define MOD (1000003ll)
#define LIMIT (1100000)
template < typename T = int >
inline T read(void);
int A, B;
int N, gcdv;
ll ans(0);
ll pow2[LIMIT + 100];
basic_string < int > Prime;
bitset < LIMIT + 100 > notPrime;
struct Num{int v; int cnt;};
basic_string < Num > fact;
ll qpow(ll a, ll b){
ll ret(1), mul(a);
while(b){
if(b & 1)ret = ret * mul % MOD;
b >>= 1;
mul = mul * mul % MOD;
}return ret;
}
void Init(int x){
fact.clear();
for(auto p : Prime){
if(p * p > x)break;
if(x % p == 0)fact += {p, 0};
while(x % p == 0)fact.back().cnt++, x /= p;
}if(x != 1)fact += {x, 1};
}
void dfs(int dep = 0, ll d = 1, ll base = 1, ll div = 1){
if(dep == (int)fact.size())
return (ans += pow2[gcdv * (N / d)] * (d / div * base) % MOD) %= MOD, void();
dfs(dep + 1, d, base, div);
base *= (fact.at(dep).v - 1), div *= fact.at(dep).v;
for(int i = 1; i <= fact.at(dep).cnt; ++i)
d *= fact.at(dep).v, dfs(dep + 1, d, base, div);
}
int main(){
for(int i = 2; i <= LIMIT; ++i){
if(!notPrime[i])Prime += i;
for(auto p : Prime){
if(p * i > LIMIT)break;
notPrime[p * i] = true;
if(i % p == 0)break;
}
}
pow2[0] = 1;
for(int i = 1; i <= LIMIT; ++i)pow2[i] = pow2[i - 1] * 2 % MOD;
int T = read();
while(T--){
A = read(), B = read();
N = (A + B) / __gcd(A, B), gcdv = __gcd(A, B);
Init(N);
ans = 0;
dfs();
(ans *= qpow(N, MOD - 2)) %= MOD;
printf("%lld\n", (pow2[A + B] - ans + MOD) % MOD);
}
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
template < typename T >
inline T read(void){
T ret(0);
int flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
例题 #8 LG-P4916 [MtOI2018]魔力环
题面
你需要对长度为 $ n $ 的环黑白染色，要求染 $ m $ 个黑色与 $ n - m $ 个白色，并要求不能有超过 $ k $ 个黑色相邻，求本质不同方案数。
Solution
纯组合意义是不可能的，这辈子都不可能的。
发现本质不同关键字，不难想到群论，对于本题可以使用 Burnside，考虑令 $ g(i) $ 表示置换为旋转 $ i $ 的不动点的数量，令 $ f(i) $ 表示存在 $ i $ 个环的方案数，这样答案不难想到即为：
考虑经典转化，即 $ f(i) = g(\gcd(n, i)) $。
转化为：
考虑处理 $ f(d) $，令 $ \xi(n, m, k) $ 表示 $ n + m $ 个球染 $ m $ 个黑色限制为 $ k $ 的方案数，由将 $ m $ 个球可空地放入 $ n $ 个盒每个盒不能超过 $ k $ 的方案数得到，不难想到一个类似二项式反演的容斥：
即经典插板法。
则对于 $ f(d) $，应有：
同时注意对于 $ d \nmid m $，显然 $ f(d) = 0 $。
Code
#define _USE_MATH_DEFINES
#include <bits/stdc++.h>
#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW void* Edge::operator new(size_t){static Edge* P = ed; return P++;}
#define ROPNEW_NODE void* Node::operator new(size_t){static Node* P = nd; return P++;}
using namespace std;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;
#define MOD (998244353ll)
#define LIM (210000)
template < typename T = int >
inline T read(void);
int N, M, K;
ll phi[LIM + 100];
bitset < LIM + 100 > notPrime;
basic_string < int > Prime;
ll fact[LIM + 100], inv[LIM + 100];
int main(){
auto qpow = [](ll a, ll b)->ll{
ll ret(1), mul(a);
while(b){
if(b & 1)ret = ret * mul % MOD;
b >>= 1;
mul = mul * mul % MOD;
}return ret;
};
auto Init = [qpow](void)->void{
phi[1] = fact[0] = 1;
for(int i = 2; i <= LIM; ++i){
if(!notPrime[i])phi[i] = i - 1, Prime += i;
for(auto p : Prime){
if((ll)i * p > LIM)break;
notPrime[i * p] = true;
if(i % p == 0)phi[i * p] = p * phi[i] % MOD;
else phi[i * p] = phi[p] * phi[i] % MOD;
if(i % p == 0)break;
}
}
for(int i = 1; i <= LIM; ++i)fact[i] = fact[i - 1] * i % MOD;
inv[LIM] = qpow(fact[LIM], MOD - 2);
for(int i = LIM - 1; i >= 0; --i)inv[i] = inv[i + 1] * (i + 1) % MOD;
};Init();
auto GetC = [](ll n, ll m)->ll{
if(n < m || n < 0 || m < 0)return 0;
return fact[n] * inv[m] % MOD * inv[n - m] % MOD;
};
auto Cal = [qpow, GetC](ll N, ll M, ll K)->ll{
ll ret(0);
for(int i = 0, flag = 1; i * (K + 1) <= M; ++i, flag *= -1)
(ret += ((flag * GetC(N, i) * GetC(M - i * (K + 1) + N - 1, N - 1) % MOD) + MOD) % MOD) %= MOD;
(ret *= (N + M) * qpow(N, MOD - 2) % MOD) %= MOD;
return ret;
};
ll ans(0);
N = read(), M = read(), K = read();
if(N == M)printf("%d\n", K >= N ? 1 : 0), exit(0);
for(int i = 1; i <= N; ++i)
if(N % i == 0 && M % i == 0)
(ans += Cal((N - M) / i, M / i, K) * phi[i] % MOD) %= MOD;
(ans *= qpow(N, MOD - 2)) %= MOD;
printf("%lld\n", ans);
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
template < typename T >
inline T read(void){
T ret(0);
int flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
后面就是烷烃计数烯烃计数等一大堆阴间东西，省选之后再来写~
UPD
update-2023_01_06 初稿
update-2023_01_09 fix大量笔误及不严谨的地方 补充了部分证明
update-2023_01_10 重写轨道-稳定子定理的证明
update-2023_02_04 调整部分排版
update-2023_02_06 添加例题 #5 #6 #7
update-2023_02_16 添加半群等内容 添加双半群模型
update-2023_03_06 添加例题 #8
