LG-P3562 [POI2013] LAS-Laser 题解
LG-P3562 [POI2013] LAS-Laser Solution
更好的阅读体验戳此进入
(建议您从上方链接进入我的个人网站查看此 Blog,在 Luogu 中图片会被墙掉,部分 Markdown 也会失效)
题面
给定平面上的 $ n $ 条线段(用点 $ (x_1, y_1), (x_2, y_2) $ 表示),你可以从原点引出最多 $ k $ 条射线,使其穿过尽可能多的线段,且每条线段最多被穿过 $ 1 $ 次,求最多可以穿过多少条线段。
$ 1 \le n \le 5 \times 10^5, 1 \le k \le 100, 1 \le x_1, y_1, x_2, y_2 \le 10^5 $。
输入格式
$ n, k $
$ x_1, y_1, x_2, y_2 $
$ \cdots $ (n lines in total)
Solution
首先本题有一个比较显而易见的贪心,即最优的情况下每条射线至少穿过一条线段的端点,感性理解一下,如果不穿过端点那么移动到端点一定是不劣的。
我们可以考虑一个类似极角排序的思想,把每一个点当成一个向量的坐标表示,按照角度进行排序离散化并尝试寻找性质:
可以看下图:
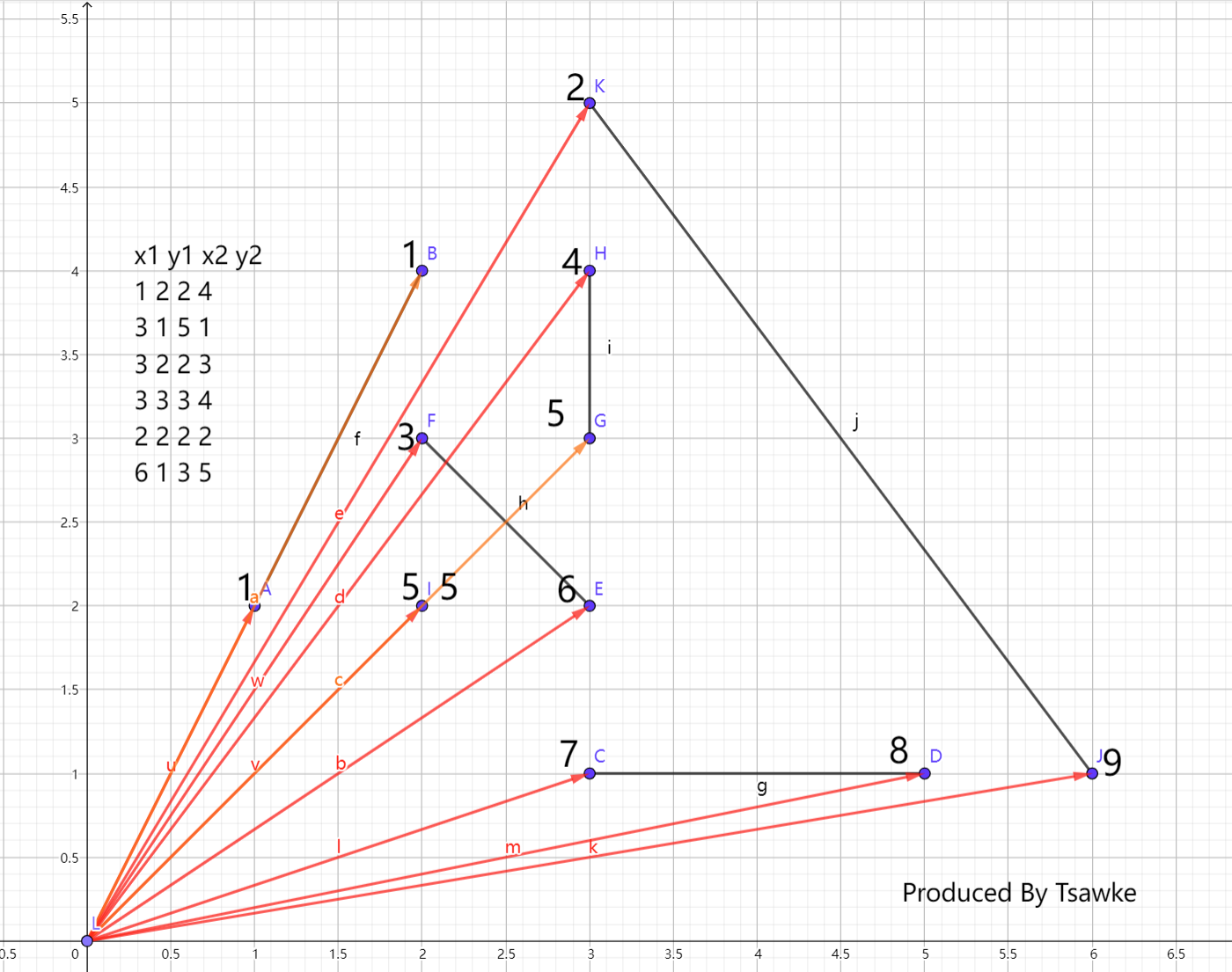
排序离散化后,每个点旁边的数字即为其离散化后的坐标,于是我们发现,每一条线段都变成了一个区间:
$ \left[ 1, 1 \right], \left[ 7, 8 \right], \left[ 3, 6 \right], \left[ 4, 5 \right], \left[ 5, 5 \right], \left[ 2, 9 \right] $。
同时注意,离散化后的每一个点都是至少一个区间的端点!
而我们从原点引出的每一条射线,也可以抽象成一个向量的坐标,或者换句话说,是这些区间中的一个点。
于是此时我们便可以发现问题变成了在给定区间中选择一些点,使这些点涉及的区间尽可能多,且每个区间中最多只有一个点。
对于这个问题应该是一个显然的 DP,我们考虑设 $ dp(i, j) $ 表示在前 $ i $ 个点(等同于区间端点)中选择 $ j $ 个点最多可以涉及多少个区间。
考虑转移,显然可以通过 $ dp(i - 1, j) $ 转移,同时我们也可以考虑如果选择第 $ i $ 个点,那么应该从什么区间转移而来?
显然选择第 $ i $ 个点后,其所涉及的所有区间都不能有其它的点,所以我们应该记录 $ i $ 所涉及的所有的区间中最左的端点,记其为 $ lft(i) $,同时记点 $ i $ 涉及的区间的数量为 $ cnt(i) $,那么也就是从 $ dp(lft(i) - 1, j - 1) + cnt(i) $ 转移而来。
于是我们的方程便为 $ dp(i, j) = \max(dp(i - 1, j), dp(lft(i) - 1, j - 1) + cnt(i)) $。
通过差分预处理一下 $ lft $ 和 $ cnt $ 即可。
然后注意观察到 $ i $ 的值域是 $ 5 \times 10^5 \(,\) j $ 的值域是 $ 10^2 $,所以空间占用为 $ \dfrac{5 \times 10^5 \times 10^2 \times 4}{1024^2} \gt 128 $,空间会炸,发现 $ j $ 只会从 $ j $ 或 $ j - 1 $ 转移而来,所以可以以类似写背包时候的思想把 $ j $ 的维度去掉,将不同版本考虑好即可。
时间复杂度是 $ O(n(\log n + k)) $ 的,显然可以通过。
Tips:对于具体的离散化实现,可以通过向量的外积,大于零则前者在后者的顺时针方向,反之亦然,可以考虑写个结构体重载小于号和等于号,或者在 sort 和 unique 和 lower_bound 的时候写个 lambda 函数也行,亦或自己纯手搓一个离散化也可以实现,具体可以看代码。
Code
#define _USE_MATH_DEFINES
#include <bits/extc++.h>
#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW(arr) void* Edge::operator new(size_t){static Edge* P = arr; return P++;}
/******************************
abbr
segl => line segment
lft => left
******************************/
using namespace std;
using namespace __gnu_pbds;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;
template<typename T = int>
inline T read(void);
struct Point{
int x, y;
friend ll operator * (const Point &a, const Point &b){
return (ll)a.x * b.y - (ll)a.y * b.x;
}
friend bool operator < (const Point &a, const Point &b){
return a * b < 0;
}
friend bool operator == (const Point &a, const Point &b){
return a * b == 0;
}
};
int K, N;
pair < Point, Point > segl[510000];
pair < int, int > seg[510000];
vector < Point > arr;
int cnt[1100000];
int lft[1100000];
int dp[1100000];
int main(){
K = read(), N = read();
for(int i = 1; i <= N; ++i){
int x1 = read(), y1 = read(), x2 = read(), y2 = read();
segl[i] = {Point{x1, y1}, Point{x2, y2}};
arr.push_back(Point{x1, y1}), arr.push_back(Point{x2, y2});
}
sort(arr.begin(), arr.end(), [](const Point &a, const Point &b)->bool{return a * b < 0;});
auto endpos = unique(arr.begin(), arr.end());
int siz = distance(arr.begin(), endpos);
for(int i = 1; i <= N; ++i){
seg[i].first = distance(arr.begin(), lower_bound(arr.begin(), endpos, segl[i].first) + 1);
seg[i].second = distance(arr.begin(), lower_bound(arr.begin(), endpos, segl[i].second) + 1);
if(seg[i].first > seg[i].second)swap(seg[i].first, seg[i].second);
}
for(int i = 1; i <= siz; ++i)lft[i] = siz;
for(int i = 1; i <= N; ++i){
++cnt[seg[i].first], --cnt[seg[i].second + 1];
lft[seg[i].second] = min(lft[seg[i].second], seg[i].first);
}
for(int i = 1; i <= siz; ++i)cnt[i] += cnt[i - 1];
for(int i = siz - 1; i >= 1; --i)lft[i] = min(lft[i], lft[i + 1]);
for(int j = 1; j <= K; ++j){
for(int i = siz; i >= 1; --i)dp[i] = max(dp[i], dp[lft[i] - 1] + cnt[i]);
for(int i = 1; i <= siz; ++i)dp[i] = max(dp[i], dp[i - 1]);
}
printf("%d\n", dp[siz]);
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
template<typename T>
inline T read(void){
T ret(0);
short flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
UPD
update-2022_10_04 初稿

