LG-P3563 [POI2013]POL-Polarization 题解
LG-P3563 [POI2013]POL-Polarization Solution
更好的阅读体验戳此进入
(建议您从上方链接进入我的个人网站查看此 Blog,在 Luogu 中图片会被墙掉,部分 Markdown 也会失效)
题面
给定一棵有 $ n $ 个节点的树,要求将树上所有边变成有向边,求本质不同连通点对的最小和最大对数。
定义本质不同连通点对为对于点 $ a, b $,满足 $ a $ 能到达 $ b $,或 $ b $ 能到达 $ a $。
$ n \le 2.5 \times 10^5 $。
Solution
该说不说这道题的数据有点水,可以微调块长然后用一个不正确的贪心水过去。。。
首先对于第一个问题应该比较简单,如果说的专业一点就是,树是一个二部图,将其分解为左右部图后,把部图间的无向边全部改为左部图向右部图的有向边(反之亦然),则最小值一定为 $ n - 1 $。
或者通俗地说,把 $ i $ 到 $ i + 1 $ 层之间的边和 $ i + 1 $ 到 $ i + 2 $ 层之间的边反向连结,最终一定有 $ n - 1 $ 对连通点对。
对于第二个问题需要引入几个我不会证明很神奇的 Lemma:
Lemma 1:对于一个使连通点对数量最多的图,其中一定至少有一个点满足以其为根,所有子树要么是外向的要么是内向的,也就是说要么全部指向根方向,要么全部背向根方向。
Lemma 2:对于一个使连通点对数量最多的图,Lemma 1 的这个点一定在树的任意一个重心上。
证明:The proof is left to the reader. (不会证)
于是我们便可以发现,这道题的思路就是找到树的重心,然后以重心为根搜一下其每个子树的大小,记录下来之后枚举哪些子树是外向的,哪些是内向的,才会使最终答案最优。
如果是菊花图的话子树个数最多是 $ n $ 级别的,那么嗯枚举的话大概是 $ O(2^n) $ 显然不可以通过,考虑优化。
首先我们接着刚才的思路往下想此时我们根已经确定了,假设我们有这样一个图:
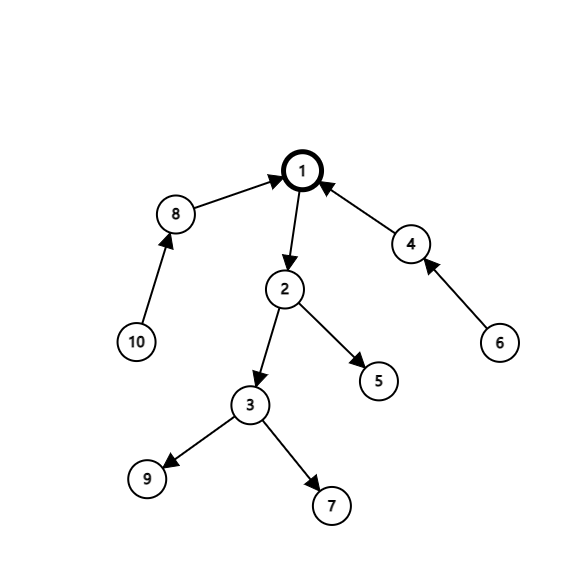
我们考虑除了根节点外的每一个节点,不难发现我们现在若仅考虑对每一个节点和该节点的所有子节点最高到达该节点的父亲的连通对,那么如果我们令节点 $ i $ 为根的子树大小为 $ siz_i $,那么显然上述的所有联通对的个数为 $ \sum siz_i $。
在这之后我们便不难发现只剩下如 $ (10, 3) $,即 $ 10 \rightarrow 8 \rightarrow 1 \rightarrow 2 \rightarrow 3 $,这种通过根节点的路径形成的连通对没有考虑,于是联想到我们之前的 Lemma,如果我们设所有内向的子树大小之和为 $ k_1 $,所有外向的子树大小之和为 $ k_2 $,且显然有 $ k_1 + k_2 = n - 1 $,不难想到这种情况中的连通对数量即为 $ k_1 \times k_2 $。
于是显然有 $ ans = \sum siz_i + k_1 \times k_2 $,当根确定之后前者一定是固定的,那么我们就只需要考虑什么时候后者最大即可。
我们将所有子树大小抽象成一个序列,那么我们的目标就是要将这个序列分成两部分,使两部分分别求和后乘积最大。两个数和固定,要让积最大,这玩意应该很显然就是要让两个数相等吧,放到这道题上就是让两部分的求和后的差值最小,这东西不觉得非常像搭建双塔吗。。。关于一个人类智慧的DP - Vijos 1037 搭建双塔
不过我们仔细观察一下后发现实际上并不一样,本题里我们需要将所有的数都用上,且搭建双塔的时间复杂度放在这题上就很离谱了。
首先这里提供一个奇怪的贪心,据说是 2015 集训队论文里的(虽然我没找到)(而且是错误的),大概就是维护一个大根堆,然后每次取堆顶的两个值,计算它们差的绝对值然后再插入堆里,当堆中剩余一个元素的时候这个元素就是差值的最小值,看起来似乎很奇怪,细想一下似乎很正确,但是这是错误的(如果不是我想错了的话)。
这个贪心大概的思路就是每次找最大的两个分别放在两侧,会有一个差值,然后我们可以将这个差值也认为是一个新的数,显然差值也可以和普通的数一样放置,比如说两对差值为 $ 1 $ 的块全部拼在一起最终的差值也就是 $ 0 $ 了,这里如果你做过搭建双塔的话大概也就能看出来错误在哪里了,显然我们贪心地取两个最大的放在两侧并不一定是最优的,比如这样一个序列:$ 3, 3, 3, 3, 3, 3, 3, 3, 8, 8, 8 $,显然 $ 8 $ 放在一起,$ 3 $ 放在一起,最终差值为 $ 0 $,但是按照这个贪心则会优先把两个 $ 8 $ 放在一起抵消,导致最后剩下的差值为 $ 2 $。
但是这个东西是可以过的,可以发现如果进行根号分治,但是不按照 $ \sqrt{n} $ 分治而是固定按照 $ 1000 $ 的话,那么刚好可以把这个贪心不正确的数据点在时间复杂度允许的情况下用正常的 DP + bitset 求解,最后无论是 Luogu 的十个数据点还是原题的六十多个数据点都是可以 Accept 的,就算按照标准的根号分支也可以过接近 $ 90% $ 的点,不过不能怪数据弱,确实这个是很难卡的。
Code:
const int B = 1000;//int(sqrt(N));
if(tot >= B){
std::priority_queue < int, vector < int >, less < int > > vals;
for(auto i : subt)vals.push(i);
while(vals.size() != 1){
int x = vals.top(); vals.pop();
int y = vals.top(); vals.pop();
vals.push(abs(x - y));
}
int diff = vals.top();
int vx = (N - 1 - diff) / 2;
int vy = vx + diff;
ans += (ll)vx * vy;
}else{
dp[0] = true;
for(auto i : subt)dp |= dp << i;
for(int i = N / 2 + 1; i >= 0 ; --i)if(dp[i]){ans += (ll)i * (N - i - 1); break;}
}
考虑正解,开一个大小为 $ n $ 的 bool 类型数组,表示 $ k_1 $ 是否能为 $ i $(或表示 $ k_2 $ 同理)显然是一个 $ O(n^2) $ 的 DP,转移之后从 $ \dfrac{n}{2} $ 开始跑,跑到的第一个可行解一定为最优解,使两者差最小,但是这个复杂度显然不正确。考虑子树的个数,如果小于 $ \sqrt{n} $ 那么显然这个复杂度实际上是 $ O(n\sqrt{n}) $ 的,如果大于 $ \sqrt{n} $,则子树最大值一定是小于 $ \sqrt{n} $ 的,也就是一定有相同大小的子树,且随着子树个数增多,最大值会逐渐变小,导致重复的个数继续增大,此时我们可以以多重背包的思想取考虑,将多个相同大小的子树拆成 $ 2^0, 2^1, 2^1, \cdots $,变成多个背包,令大小为 $ i $ 的子树有 $ cnt_i $ 个,最后的复杂度大概是一个 $ O(n\sum \log cnt_i) $,这个东西大概使介于 $ O(n\log n) $ 和 $ O(n\sqrt{n}) $ 之间的,具体证明我也不知道应该怎么证,感性理解一下吧。
然后发现复杂度依然不正确,考虑把这个数组压成一个 bitset,这样在进行或运算的时候还可以大幅降低速度,最终是 $ O(\dfrac{n\sqrt{n}}{\omega}) $,此处的 $ \omega $ 一般为 $ 32 $,显然可以通过。
Code
#define _USE_MATH_DEFINES
#include <bits/extc++.h>
#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW(arr) void* Edge::operator new(size_t){static Edge* P = arr; return P++;}
using namespace std;
using namespace __gnu_pbds;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;
template<typename T = int>
inline T read(void);
struct Edge{
Edge* nxt;
int to;
OPNEW;
}ed[510000];
ROPNEW(ed);
Edge* head[260000];
int N;
int siz[260000], msiz[260000], rt(0);
void dfs(int p, int fa = -1){
msiz[p] = 0;
siz[p] = 1;
for(auto i = head[p]; i; i = i->nxt){
if(SON == fa)continue;
dfs(SON, p);
siz[p] += siz[SON];
msiz[p] = max(msiz[p], siz[SON]);
}
msiz[p] = max(msiz[p], N - siz[p]);
if(!rt || msiz[p] < msiz[rt])rt = p;
}
int cnt[260000];
int tot(0);
ll ans(0);
bitset < 260000 > dp;
int main(){
N = read();
for(int i = 1; i <= N - 1; ++i){
int s = read(), t = read();
head[s] = new Edge{head[s], t};
head[t] = new Edge{head[t], s};
}
dfs(1);
dfs(rt);
for(int i = 1; i <= N; ++i)if(i != rt)ans += siz[i];
for(auto i = head[rt]; i; i = i->nxt)cnt[siz[SON]]++;
for(int i = 1; i <= N / 2; ++i)while(cnt[i] > 2)cnt[i] -= 2, cnt[i * 2]++;
dp[0] = true;
for(int i = 1; i <= N; ++i)while(cnt[i]--)dp |= dp << i;
for(int i = N / 2; i >= 0 ; --i)if(dp[i]){ans += (ll)i * (N - i - 1); break;}
printf("%d %lld\n", N - 1, ans);
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
template<typename T>
inline T read(void){
T ret(0);
short flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
UPD
update-2022_09_28 初稿

