FFT & NTT - 快速傅里叶变换 & 快速数论变换
FFT & NTT - 快速傅里叶变换 & 快速数论变换
更好的阅读体验戳此进入
（建议您从上方链接进入我的个人网站查看此 Blog，在 Luogu 中图片会被墙掉，部分 Markdown 也会失效）
写在前面
该博客仅为记录学习中的笔记及个人理解，不保证正确性，同时欢迎各位纠正。
图片没有放在图床上，全都是丢在自己的网站上，带宽较低可能加载较慢。
目的
FFT (Fast Fourier Transform) 是为了为快速求出两个多项式的卷积，也就是 $ C(x) = A(x) \ast B(x) $ ，或者表达为
( $ a(i), b(i), c(i) $ 为多项式系数 $ A(x), B(x), C(x) $ 为多项式 )
前置知识
原根
详细定义可参考 知乎 或 OI-WIKI，简而言之就是，对于模 $ m $ 意义下的原根 $ a $，有 $ a^1, a^2, \cdots, a^{\varphi(m)} \bmod m $ 的值各不相同，$ \varphi(m) $ 表示 欧拉函数 。
单位根
对于 $ \epsilon^n = 1 (\epsilon \neq 1)$，称 \(\epsilon\) 为 $ n $ 次单位根，其可以为模意义下的或复数意义下的。
模意义下的（原根）
对于模 $ m $ 意义下的， $ m $ 为质数，令原根为 $ g $ 则有 $ \gcd(g, m) = 1 $，此时若满足 $ n \mid m - 1 $ 则有 $ \epsilon = g^{\frac{m - 1}{n}} $。
更通俗一点的描述，也就是对于所有 $ d \le m - 2 $ 有 $ \epsilon^d \bmod{m} $ 各不相同。
证明：
由 费马小定理 可知显然成立
复数意义下的
对于复数意义下的，则可将一单位圆 n 等分，并取该 n 个点表示的复数，从 x 轴，也就是从 $ (1, 0) $ 开始取，逆时针从 0 开始对这些复数进行编号，对于第 k 个复数记作 $ \epsilon_n^k $，则对于幅角非零且最小的复数 $ \epsilon_n^1 $，由复数相乘时模长相乘幅角相加可知一定有 $ (\epsilon_n1)k = \epsilon_n^k $，则称 $ \epsilon_n^1 $ 为 $ n $ 次单位根。
很多地方可能用 $ \omega $ 来表示单位根，也就是本文中的 $ \epsilon $，仅为表示方式的区别而已。
单位根性质
对于复数意义下的 $ n $ 次单位根有如下式子
证明
单位根求法
复数意义下
由单位根的定义显然可知对于 n 次单位根的 k 次方，即 $ \omega_n^k $，考虑用三角函数表达，有 $ \omega_n^k = cos(2\pi \div n \times k) + sin(2\pi \div n \times k)i $。
模意义下的（原根）
因为 NTT 模数的原根一般都很小，只有极少数的质数的原根能达到 20，所以可以直接按照定义，考虑遍历所有 $ d \le m - 2 $，如果不存在 $ d \equiv 1 (\bmod{m}) $ 则其为原根。
同时还存在一种效率更高的方式，考虑将 $ m - 1 $ 质因数分解，对于其每一个质因子 $ p_i $ ，及一个数 $ \epsilon $，判断是否满足 $ \epsilon^{\frac{m - 1}{p_i}} \equiv 1 (\bmod{m})$ ，满足则 $ \epsilon $ 为原根。
等比数列求和公式
正文
单位根反演
对于 $ n $ 次单位根 $ \epsilon $，显然有如下的， $ a_1 = \epsilon^0 = 1 $， $ q = \epsilon^v $，的等比数列的求和为
又有 $ n $ 次单位根性质可知 $ \epsilon^v = 1 $ 时，上式 $ = 1 $。
且又有如下式子
综上则有如下式子
此即为单位根反演
推式子
将单位根反演代入原式，令 $ v = p + q - i $，则 $ n \mid v $，
且令
显然有如下式子
观察最后两个式子，可以发现如下两个式子
考虑令该多项式上一点为 $ (\epsilon^p, f(p)) $，多项式第 $ p $ 项系数为 $ g(p) $，有
证明
则可知求 $ f(p) $ 的过程即为DFT，求 $ g(p) $ 的过程即为IDFT。
由定义显然有
（ $ A, B, C $ 均代表该多项式 ）
又有
证明
则此时多项式 C 可求，但时间复杂度仍然是 $ O(n^2) $
继续推式子
对于
可以考虑 $ f(p) $ 与 $ f(p + 2^k) $ 的关系，则此时我们可以假设 $ n = 2^{k + 1} $
且令
由单位根的性质可以得到以下式子
其中u为一个二次单位根，因为显然当且仅当 $ i $ 为奇数时，下式不为 $ 0 $。
$ i $ 为奇数时，可以有如下推导
此时显然有
且我们已知 $ \epsilon $ 为 $ 2^{k + 1} $ 次单位根，所以显然有
所以 $ \epsilon{2k} $ 为二次单位根，这里为了方便，我们用 $ u $ 代替。
此时可以考虑令
所以将幂次除以二后，显然有（此时 $ \epsilon $ 应为 $ \dfrac{n}{2} $ 次单位根）
再将式子转化为
此时式子形式便可按相同方法继续递归，直到 $ n = 2 $ 时进行回溯。
Code
#define _USE_MATH_DEFINES
#include <bits/stdc++.h>
#define PI M_PI
#define E M_E
#define DFT true
#define IDFT false
#define eps 1e-6
#define comp complex < double >
/******************************
abbr
pat -> pattern
pol/poly -> polynomial
omg -> omega
******************************/
using namespace std;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
class Polynomial{
private:
int lena, lenb;
int len;
comp A[1100000], B[1100000];
public:
comp Omega(int, int, bool);
void Init(void);
void FFT(comp*, int, bool);
void MakeFFT(void);
}poly;
template<typename T = int>
inline T read(void);
int main(){
poly.Init();
poly.MakeFFT();
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
void Polynomial::MakeFFT(void){
FFT(A, len, DFT), FFT(B, len, DFT);
for(int i = 0; i <= len; ++i)A[i] *= B[i];
FFT(A, len, IDFT);
for(int i = 0; i <= lena + lenb - 2; ++i)
printf("%d%c", int(A[i].real() / len + eps + 0.5), i == lena + lenb - 1 ? '\n' : ' ');
}
void Polynomial::FFT(comp* pol, int len, bool pat){
if(len == 1)return;
comp sA[len / 2 + 10], sB[len / 2 + 10];
for(int i = 0; i <= len / 2 - 1; ++i){
sA[i] = pol[i * 2];
sB[i] = pol[i * 2 + 1];
}
FFT(sA, len / 2, pat), FFT(sB, len / 2, pat);
for(int i = 0; i <= len / 2 - 1; ++i){
comp omg = Omega(len, i, pat);
pol[i] = sA[i] + omg * sB[i];
pol[i + len / 2] = sA[i] - omg * sB[i];
}
}
void Polynomial::Init(void){
lena = read(), lenb = read();
for(int i = 0; i <= lena; ++i)A[i].real((double)read());
for(int i = 0; i <= lenb; ++i)B[i].real((double)read());
len = 1;
lena++, lenb++;
while(len <= lena + lenb)len <<= 1;
}
comp Polynomial::Omega(int n, int k, bool pat){
if(pat == DFT)return comp(cos(2 * PI * k / n), sin(2 * PI * k / n));
return conj(comp(cos(2 * PI * k / n), sin(2 * PI * k / n)));
}
template<typename T>
inline T read(void){
T ret(0);
short flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
优化
显然递归版本的写法虽然更容易理解，但每层都需要开额外的数组，消耗空间很大，时间也较大，虽然可以通过 洛谷模板，但是在后面的题里可能会被卡常，于是便有了如下的优化，即 $ \text{Cooley - Tukey} $ 算法。
首先观察如下递归过程（ 图片来源 ）
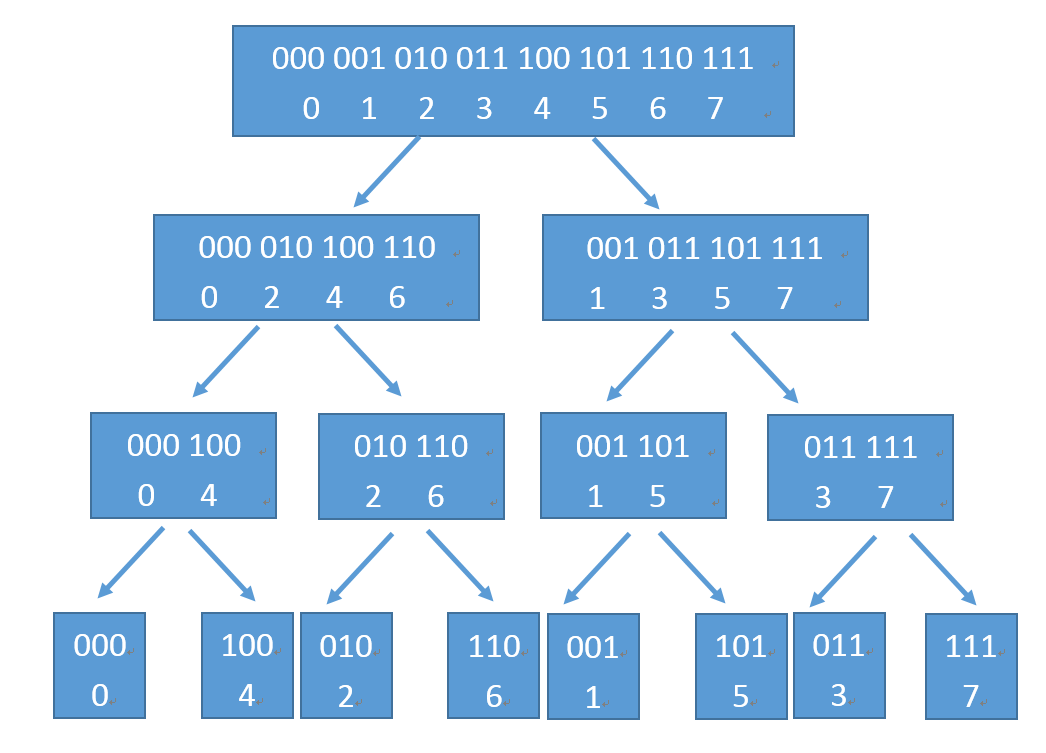
通过观察我们即可发现（这真是人类能想出来的吗）对于每一个数的位置，显然是进行了一次二进制的反转，如 1 的位置从 001 变成了 100，那么我们便可以利用这个性质对位置进行反转。
这里提供两种写法
$ O(nlogn) $
int size(0);
while((1 << size) < len - 1)++size;
for(int i = 0; i <= len - 1; ++i){
int tmp(0);
for(int j = 0; j <= size; ++j){
if((1 << j) & i) tmp |= (1 << (size - j - 1));
}
if(i < tmp)swap(pol[i], pol[tmp]);
}
类似于模拟的写法，首先判断二进制数的位数，即 size，然后对于每个数按位判断，并将其转移到 tmp 的对应位置，最后通过swap交换位置， $ i < tmp $ 的判断是为了使其只会交换一次。
$ O(n) $
int pos[len + 10];
memset(pos, 0, sizeof(pos));
for(int i = 0; i < len; ++i){
pos[i] = pos[i >> 1] >> 1;
if(i & 1)pos[i] |= len >> 1;
}
for(int i = 0; i < len; ++i)if(i < pos[i])swap(pol[i], pol[pos[i]]);
这种方法我就不严格地证明了（主要我也不会），就从找规律的角度来研究一下这个线性递推的式子。
举个例子，假设我们有一个二进制数 $ 0101110 $ 我们想要对其进行 Reverse，因为我们要进行递推，所以需要分解为子问题，可以考虑将其右移一位，即变为 $ 0010111 $，然后 Reverse，变为 $ 1110100 $，在对比我们想要求得的 $ 0111010 $，发现前者去掉最后一位，后者忽略第一位是完全相同的，那么将前者右移一位后在考虑最前面一位是 $ 1 $ 还是 $ 0 $ 即可。
对于 Reverse 后合并的过程显然我们可以通过从倒数第二层开始，模拟递归形式的操作，这部分较为显然便不再赘述。
值得注意的一个点是当我们更新数组时，由于非递归写法，可能会对需要用到的变量进行覆盖，所以这时我们显然可以将原数组复制一份，这样的空间时可以接受的，当然更好的做法就是将会被覆盖的那个变量存起来再进行操作，如下。
Reverse(pol, len);
for(int size = 2; size <= len; size <<= 1){
for(comp* p = pol; p != pol + len; p += size){
int mid(size >> 1);
for(int i = 0; i < mid; ++i){
auto tmp = Omega(size, i, pat) * p[i + mid];
p[i + mid] = p[i] - tmp;
p[i] = p[i] + tmp;
}
}
}
最后贴上优化后的完整代码
#define _USE_MATH_DEFINES
#include <bits/stdc++.h>
#include <mmintrin.h>
#define PI M_PI
#define E M_E
#define DFT true
#define IDFT false
#define eps 1e-6
#define comp complex < double >
/******************************
abbr
pat -> pattern
pol/poly -> polynomial
omg -> omega
******************************/
using namespace std;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
class Polynomial{
private:
int lena, lenb;
int len;
comp A[2100000], B[2100000];
public:
comp Omega(int, int, bool);
void Init(void);
void FFT(comp*, int, bool);
void Reverse(comp*);
void MakeFFT(void);
}poly;
template<typename T = int>
inline T read(void);
int main(){
poly.Init();
poly.MakeFFT();
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
void Polynomial::MakeFFT(void){
FFT(A, len, DFT), FFT(B, len, DFT);
for(int i = 0; i <= len; ++i)A[i] *= B[i];
FFT(A, len, IDFT);
for(int i = 0; i <= lena + lenb - 2; ++i)
printf("%d%c", int(A[i].real() / len + eps + 0.5), i == lena + lenb - 2 ? '\n' : ' ');
}
void Polynomial::Reverse(comp* pol){
int pos[len + 10];
memset(pos, 0, sizeof(pos));
for(int i = 0; i < len; ++i){
pos[i] = pos[i >> 1] >> 1;
if(i & 1)pos[i] |= len >> 1;
}
for(int i = 0; i < len; ++i)if(i < pos[i])swap(pol[i], pol[pos[i]]);
}
void Polynomial::FFT(comp* pol, int len, bool pat){
Reverse(pol);
for(int size = 2; size <= len; size <<= 1){
for(comp* p = pol; p != pol + len; p += size){
int mid(size >> 1);
for(int i = 0; i < mid; ++i){
auto tmp = Omega(size, i, pat) * p[i + mid];
p[i + mid] = p[i] - tmp;
p[i] = p[i] + tmp;
}
}
}
}
void Polynomial::Init(void){
lena = read(), lenb = read();
for(int i = 0; i <= lena; ++i)A[i].real((double)read());
for(int i = 0; i <= lenb; ++i)B[i].real((double)read());
len = 1;
lena++, lenb++;
while(len <= lena + lenb)len <<= 1;
}
comp Polynomial::Omega(int n, int k, bool pat){
if(pat == DFT)return comp(cos(2 * PI * k / n), sin(2 * PI * k / n));
return conj(comp(cos(2 * PI * k / n), sin(2 * PI * k / n)));
}
template<typename T>
inline T read(void){
T ret(0);
short flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
NTT
前面我们已知 FFT 是在复数意义下利用单位复根的性质进行优化，而 NTT 则是在模意义下的，对于模意义下的单位根替代品则为原根，至于证明这里不再赘述，可以在 此处 查看。
而对于如洛谷模板题的这种答案系数较小的，我们可以考虑用 NTT 代替 FFT 以大量减少时间空间消耗，我们只需要找到一个比最大的答案（ $ 9 \times 9 \times 10^6 $ ）更大且是 NTT质数（或者叫费马质数），如最常见的 $ 998244353 $ 即可，其原根为 $ 3 $，如何求原根可以在前置知识中找到。
实现过程中只需要根据结论，用原根代替单位根，如将 $ \omega_n $ 用 $ g^{\frac{MOD - 1}{size}} $ 代替，将原本的共轭复数作为逆元，变为直接用费马小定理，通过快速幂求逆元，这里需要注意在最后需要把原本的 $ A(i) \div len $ 变为 $ A(i) \times inv(len) \bmod{MOD} $。
Code:
#define _USE_MATH_DEFINES
#include <bits/stdc++.h>
#include <mmintrin.h>
#define PI M_PI
#define E M_E
#define DFT true
#define IDFT false
#define eps 1e-6
#define MOD 998244353
/******************************
abbr
pat -> pattern
pol/poly -> polynomial
******************************/
using namespace std;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
ll kpow(int a, int b){
ll ret(1ll), mul((ll)a);
while(b){
if(b & 1)ret = (ret * mul) % MOD;
b >>= 1;
mul = (mul * mul) % MOD;
}
return ret;
}
class Polynomial{
private:
int lena, lenb;
int len;
int g, inv_g;
int A[2100000], B[2100000];
public:
int Omega(int, int, bool);
void Init(void);
void NTT(int*, int, bool);
void Reverse(int*);
void MakeNTT(void);
}poly;
template<typename T = int>
inline T read(void);
int main(){
poly.Init();
poly.MakeNTT();
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
void Polynomial::MakeNTT(void){
NTT(A, len, DFT), NTT(B, len, DFT);
for(int i = 0; i <= len; ++i)A[i] = ((ll)A[i] * B[i]) % MOD;
NTT(A, len, IDFT);
int mul_inv = kpow(len, MOD - 2);
for(int i = 0; i <= lena + lenb - 2; ++i)
printf("%d%c", (ll)A[i] * mul_inv % MOD, i == lena + lenb - 2 ? '\n' : ' ');
}
void Polynomial::Reverse(int* pol){
int pos[len + 10];
memset(pos, 0, sizeof(pos));
for(int i = 0; i < len; ++i){
pos[i] = pos[i >> 1] >> 1;
if(i & 1)pos[i] |= len >> 1;
}
for(int i = 0; i < len; ++i)if(i < pos[i])swap(pol[i], pol[pos[i]]);
}
void Polynomial::NTT(int* pol, int len, bool pat){
Reverse(pol);
for(int size = 2; size <= len; size <<= 1){
int gn = kpow(pat == DFT ? g : inv_g, (MOD - 1) / size);
for(int* p = pol; p != pol + len; p += size){
int mid(size >> 1);
int g(1);
for(int i = 0; i < mid; ++i, g = ((ll)g * gn) % MOD){
auto tmp = ((ll)g * p[i + mid]) % MOD;
p[i + mid] = (p[i] - tmp + MOD) % MOD;
p[i] = (p[i] + tmp) % MOD;
}
}
}
}
void Polynomial::Init(void){
lena = read(), lenb = read();
for(int i = 0; i <= lena; ++i)A[i] = read();
for(int i = 0; i <= lenb; ++i)B[i] = read();
len = 1;
lena++, lenb++;
while(len < lena + lenb)len <<= 1;
g = 3;
inv_g = kpow(g, MOD - 2);
}
template<typename T>
inline T read(void){
T ret(0);
short flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
合并DFT优化
这个单独再写一个 Blog 吧，戳此进入。
写在后面
写完之后发现似乎依然没有很清晰的弄明白，然后发现有几个Blog写的更清晰易懂
一小时学会快速傅里叶变换（Fast Fourier Transform）
至于几个TODO等以后再慢慢填坑吧
UPD
update-2022_08_10 初稿
update-2022_08_17 改了一下 latex 在 cnblog 里渲染异常的问题（ luogu 里还是炸了，以后再改）
update-2022_08_17 修复 latex 在 luogu 里渲染异常的问题
update-2022_08_22 修复 latex 在 cnblog 里仍然存在的渲染异常问题
update-2022_08_22 添加了递归版程序中的 code
update-2022_08_22 进行一些小优化
update-2022_08_22 添加了非循环写法的讲解与 code
update-2022_08_22 添加了 NTT 的讲解与 code
update-2022_08_22 完善了对模意义下单位根的求法
update-2022_08_23 更改标题
update-2022_08_23 添加几个链接
update-2022_08_25 更新标题和链接
