[图论] 最短路探秘 之 全源最短路
[图论] 最短路探秘 之 全源最短路
被迫营业again
- 前置知识：
- Dijkstra算法（优先队列/堆优化）
- Bellman-Ford算法/队列优化Bellman-Ford算法（SPFA）
前言：有一个包含 n 个结点和 m 条带权边的有向图
对于单源最短路（给定一个起点s，求s到图中任意点的距离），我们熟知的算法有Dijkstra算法和Bellman-Ford算法。
那么要想求出图中所有节点对的最短路径，我们应当怎么做呢？
很容易想出思路：我们以每个点作为起点，分别做一次单源最短路，即可得到答案。对于所有边边权非负的图，我们可以使用优先队列优化的Dijkstra算法，时间复杂度为\(O(nmlogn)\)，对于稀疏图来说，在可接受的范围。但如果图中存在负权边，我们就必须使用 \(n\) 次Bellman-Ford算法，此算法效率低下，时间复杂度为\(O(n^2m)\)， 特别地，对于稠密图，复杂度达到了\(O(n^4)\)
那么有没有什么好方法能够解决这个问题呢？
一、 Floyd-Warshall 算法
1. 算法介绍
首先我们给出一种基于动态规划思想的算法——Floyd-Warshall 算法（又称Floyd算法）。该算法的创始人之一是1978年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德（Robert W. Floyd）。该算法在负权边可以存在但负环不存在时生效，时间复杂度是 \(O(n^3)\)。该算法实现简单，代码简短好理解，应用广泛。
2. 算法思路与过程
此算法基于图的邻接矩阵存储方式，利用了动态规划的思想，具体的算法思路如下：
初始图存储在一个邻接矩阵中，有直接连边的节点对对应在矩阵中的值设置为该边边权，其他全部设置为 \(+∞\)
接下来枚举节点集合 \(\{1,2,...,k\}\) （注：具体实现时只需要递增地循环枚举变量 \(k\) ）
对于任意节点对 \((i ,j)\) ，考虑从点 \(i\) 到点 \(j\) ，已知仅经过节点集合 \(\{1,2,...,k-1\}\) 的最短路径，动态规划求出仅经过节点集合 \(\{1,2,...,k\}\) 的最短路径，假设求出来的具体的最短路径是 \(p\) ，则存在以下两种情况：
① 点 \(k\) 不在路径 \(p\) 上。则从 \(i\) 到 \(j\) 仅经过节点集合 \(\{1,2,...,k\}\) 的最短路径，就是 从 \(u\) 到 \(v\) 仅经过节点集合 \(\{1,2,...,k-1\}\) 的最短路径，不用更新
②点 \(k\) 在路径 \(p\) 上。则可以利用点 \(k\) 更新答案：从 \(i\) 到 \(j\) 仅经过节点集合 \(\{1,2,...,k\}\) 的最短路径，是从 \(i\) 到 \(k\) 仅经过节点集合 \(\{1,2,...,k-1\}\) 的最短路径 \(+\) 从 \(k\) 到 \(j\) 仅经过节点集合 \(\{1,2,...,k-1\}\) 的最短路径 （注：这个叫松弛操作）
3. 状态转移方程
基于Floyd的算法过程，我们可以设计如下状态转移方程：
\(f[i,j]=min(f[i,j],f[i,k]+f[k,j])\)
其中，\(f[i,j]\) 表示从点 \(i\) 到点 \(j\) 的最短距离，点 \(k\) 是枚举的中间点
4. 核心代码示例
for(int k=0;k<n;k++)//k为中间点
for(int i=0;i<n;i++) //i为起点
for(int j=0;j<n;j++) //j为终点
dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);
5.疑难问题解析
细心的同学可能想提问，为什么我们**必须要先枚举 \(k\)，再枚举 \(i\) 和 \(j\) **呢？如果我们先枚举\(i\) 和 \(j\)，再枚举 \(k\)，这样为什么不行呢？
其实我们现在得到的这个状态转移方程可以说算是优化之后的版本
原本的状态转移方程其实是这样子的：
\(f[k,i,j]=min(f[k-1,i,j],f[k-1,i,k]+f[k-1,k,j])\)
根据动态规划的思想，\(f[k,i,j]\) 表示的是点 \(i\) 到点 \(j\) 仅经过节点集合 \(\{1,2,...,k\}\) 的最短路径，赋予 \(f[0,i,j]\) 意义以 原图对应的邻接矩阵（即一开始所说的：有直接连边的节点对对应在矩阵中的值设置为该边边权，其他全部设置为 \(+∞\)）
那么 \(f[k,i,j]\) 要么等于 \(f[k-1,i,j]\)，即从 \(i\) 到 \(j\) 的最短路根本就不经过点 \(k\) ；要么等于 \(f[k-1,i,k]+f[k-1,k,j]\)，即从 \(i\) 到 \(j\) 的最短路是从 \(i\) 到 \(k\) 仅经过节点集合 \(\{1,2,...,k-1\}\) 的最短路径\(+\)从 \(k\) 到 \(j\) 仅经过节点集合 \(\{1,2,...,k-1\}\) 的最短路径
根据动态规划的思想，\(k\) 的意义是什么？ 其实 \(k\) 枚举的动态规划的阶段，则 \(k\) 必须要放在最外层
再细说一下，由状态转移方程\(f[k,i,j]=min(f[k-1,i,j],f[k-1,i,k]+f[k-1,k,j])\) 可知，在计算 \(f[k,i,j]\) 时，要求所有的 \(f[k-1,i,j]\) 必须计算出来，即必须在从 \(k-1\) 到 \(k\) 之前，把所有的 \(f[k-1,i,j]\) 都计算一遍，否则不能更新答案，因此必须在最外层枚举 \(k\) 。
又因为观察状态转移方程可以发现，\(f[k,...]\) 仅与 \(f[k-1,...]\) 有关，所以可以略去，就有了简化版的状态转移方程：
\(f[i,j]=min(f[i,j],f[i,k]+f[k,j])\)
二、 Johnson 算法
1. 算法介绍
Johnson 算法能够在\(O(nmlogn)\)（若利用二叉堆/优先队列优化Dijkstra）的时间内解决全源最短路问题。在图为稀疏图的情况下，该算法表现比Floyd算法更优。并且该算法能够处理在负权边可以存在，负环也可以存在的图。经过Johnson算法，要么是返回图中存在负环，要么是得到所有节点对之间的最短路。但是由于算法代码实现相对较为复杂，而且应用场景不够广泛，所以并不是很常用。
2. 算法思路与过程
还记得我们一开始说的：
-
“ 那么要想求出图中所有节点对的最短路径，我们应当怎么做呢？
很容易想出思路：我们以每个点作为起点，分别做一次单源最短路，即可得到答案。对于所有边边权非负的图，我们可以使用优先队列优化的Dijkstra算法，时间复杂度为 \(O(nmlogn)\) ”
-
“ 但如果图中存在负权边，我们就必须使用 \(n\) 次Bellman-Ford算法，此算法效率低下，时间复杂度为\(O(n^2m)\) ”
考虑这样一个思路：
我们可不可以把原来的图，等价转化为一个图，使得所有的边的边权非负，并且使得新图中任意两点的最短路仍然是原图中的最短路？
很有趣的思想是不是，我们可以做一些小小的尝试，比如说，找到原图中的最小的边权，然后把所有的边的边权都加上这个最小值的绝对值？比如以下这个图：
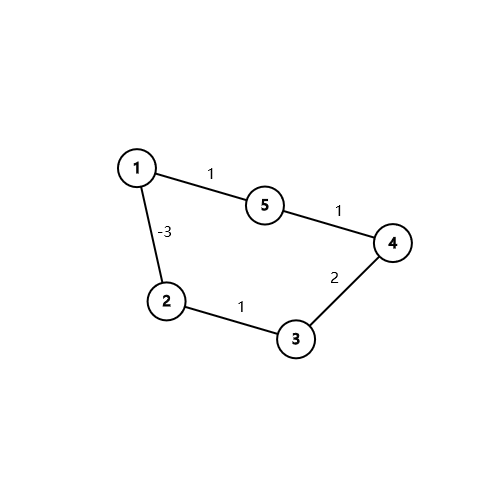
对于从点 \(1\) 到点 \(4\)，这个图的最短路应该是序列 \(1->2->3->4\)，长度为0
根据我们的思想，我们把这个图的每一条边都加上3，得到的新图如下：
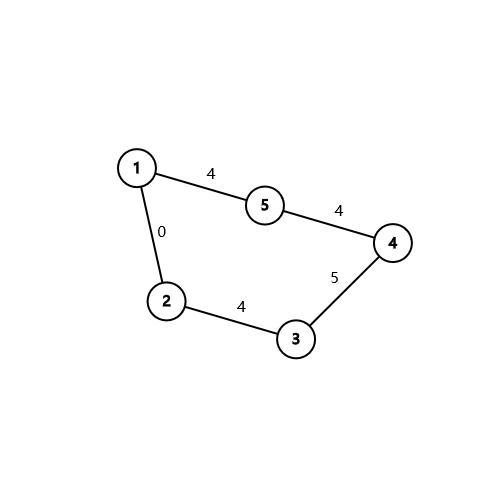
则对于新图，从点 \(1\) 到点 \(4\)，最短路应该是序列 \(1->5->4\)，长度为8
明显两个图的最短路是不一样的，所以我们的思路是错误的
那我们要怎样做，才能保证原图与新图的最短路径是一致的呢？
Johnson 算法给了下面这样的一种权值赋予方法：
在原图的基础上，新建一个虚拟节点，编号为 \(0\) ，从虚拟节点向原图中所有的点连一条边权为 \(0\) 的边
在这个图上，以节点 \(0\) 作为源点，进行一次Bellman-Ford，此时可以判断原图中是否存在负环，Bellman-Ford算法运行出来的结果，即以点 \(0\) 为源点的最短路，记在数组 \(h\) 中，\(h[u]\) 表示从点 \(0\) 到 点 \(u\) 的最短路。
用 \(w(u,v)\) 表示原图中边 \((u,v)\) 的边权，\(\hat{w}(u,v)\) 表示新图中边 \((u,v)\) 的边权
则可定义新边权如下：
\(\hat{w}(u,v)=w(u,v)+h(u)-h(v)\)
以下 \((a)\) 为原图建立虚拟节点 \(0\) 并连边，\((b)\) 为重新赋边权之后的新图
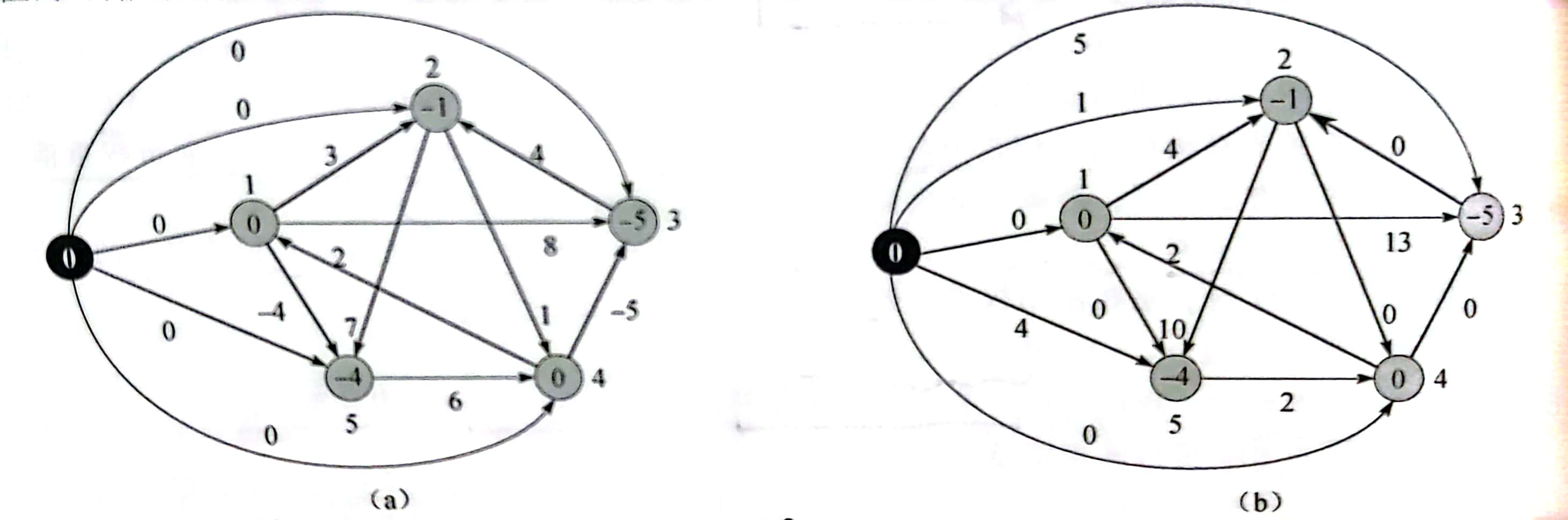
那么为什么可以这样做呢？
首先我们来证明新图边权 \(\hat{w}(u,v)\) 非负：
在对点 \(0\) 做单源最短路时，用到了松弛操作：对于节点对 \(u,v\) ，\(h(v)=min(h(v),h(u)+w(u,v))\)
所以我们可以有 \(h(v) \le h(u)+w(u,v)\)
即 \(\hat{w}(u,v)=w(u,v)+h(u)-h(v) \ge0\)，新图边权非负
接着我们来证明新图最短路径仍然是原图最短路：
对于节点对 \(u,v\) ，假设原图中的具体的最短路径为\(u->a_1->a_2->…->a_{k-1}->a_k->v\)
那么\(f(u,v)=w(u,a_1)+w(a_1,a_2)+...+w(a_{k-1},a_k)+w(a_k,v)\)，其中 \(f(u,v)\) 为原图中从 \(u\) 到 \(v\) 的最短路
若新图和原图最短路径相同的话，则\(\hat{f}(u,v)=\hat{w}(u,a_1)+\hat{w}(a_1,a_2)+...+\hat{w}(a_{k-1},a_k)+\hat{w}(a_k,v)\)，其中 \(\hat{f}(u,v)\) 为新图中从 \(u\) 到 \(v\) 的最短路
则有以下推导过程：
\(\hat{f}(u,v)=\hat{w}(u,a_1)+\hat{w}(a_1,a_2)+...+\hat{w}(a_{k-1},a_k)+\hat{w}(a_k,v)\)
\(=[w(u,a_1)+h(u)-h(a_1)]+[w(a_1,a_2)+h(a_1)-h(a_2)]+...+[w(a_{k-1},a_k)+h(a_{k-1})-h(a_k)]+[w(a_k,v)+h(a_k)-h(v)]\)
\(=w(u,a_1)+w(a_1,a_2)+...+w(a_{k-1},a_k)+w(a_k,v)+h(u)-h(v)\) （注：裂项相消求和）
\(=f(u,v)+h(u)-h(v)\)
对于给定的 \(u\) 和 \(v\) ，\(h(u)-h(v)\) 为常数，所以新图的最短路仍然是原图的最短路
（注：\(h(u)\) 的概念其实可以类比于物理中势能的概念。不管路径为何，只要确定了起点 \(u\) 和终点 \(v\) ，\(h(u)-h(v)\) 即为一个定值。把所有原来的边加上它对应的势能差，就可以把负的变成非负）
所以我们得到了解决的方法，按照上述方法可以得到 Johnson 算法的具体实现过程：
① 新建虚拟节点 \(0\) 并向所有点连权值为 \(0\) 的边
② 跑一遍Bellman-Ford最短路算法/队列优化的Bellman-Ford(SPFA)算法，解决负环问题，并求出从点 \(0\) 出发到所有点的最短路\(h[u]\)
③ 将原图中的所有边重新赋边权为 \(\hat{w}(u,v)=w(u,v)+h(u)-h(v)\)
④ 以图中每一个点为起点，分别跑一次二叉堆/优先队列优化的Dijkstra算法，求出全源最短路
注意最后要复原，即 \(w(u,v)=\hat{w}(u,v)-h(u)+h(v)\)
3. 代码示例
Johnson 算法以 Dijkstra 算法和 Bellman-Ford 算法作为子程序
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<int,int> paii;
#define N (3000+5)
int n,m,cnt[N];
bool vis[N],flag;
LL dis[N][N],h[N]; //dis[u][v]:点u到点v的最短路
vector <LL> edge[N],w[N],w2[N]; //edge:邻接表存图，w:原图边权，w2:新图边权
void add(int u,int v,int c){ //add函数:建图连边
edge[u].push_back(v);
w[u].push_back(c);
}
void create_new(int u,int v,int c){ //create_new函数:重新赋新边权
w2[u].push_back(c+h[u]-h[v]);
}
void SPFA(int be){ //SPFA:队列优化的Bellman-Ford算法
queue <int> q;
q.push(be);
memset(h,0x3f,sizeof(h));
h[be]=0,vis[be]=1;
while(!q.empty()){
int now=q.front();
q.pop();
vis[now]=0;
int len=edge[now].size();
for(int i=0;i<len;i++){
int nxt=edge[now][i];
if(h[nxt]>h[now]+w[now][i]){
h[nxt]=h[now]+w[now][i];
cnt[nxt]=cnt[now]+1;
if(cnt[nxt]>(n+1)){
flag=1;
return;
}
if(!vis[nxt]) vis[nxt]=1,q.push(nxt);
}
}
}
}
void Dijkstra(int be){ //Dijkstra算法
priority_queue<paii,vector<paii>,greater<paii> > q;
memset(vis,0,sizeof(vis));
dis[be][be]=0;
paii begin;
begin.first=0,begin.second=be;
q.push(begin);
while(!q.empty()){
paii now=q.top();
q.pop();
int u=now.second,c=now.first;
if(vis[u]) continue;
vis[u]=1;
int len=edge[u].size();
for(int i=0;i<len;i++){
int v=edge[u][i],s=w2[u][i];
if(dis[be][v]>c+s){
dis[be][v]=c+s;
if(!vis[v]){
paii nxt;
nxt.first=dis[be][v],nxt.second=v;
q.push(nxt);
}
}
}
}
}
int main(){
scanf("%d%d",&n,&m);
memset(dis,0x3f,sizeof(dis)); //初值赋为inf
for(int i=0;i<=n;i++) dis[i][i]=dis[0][i]=0;
for(int i=1;i<=m;i++){
int u,v,c;
scanf("%d%d%d",&u,&v,&c);
add(u,v,c);
}
for(int i=1;i<=n;i++){ //0号节点向其他点连边，边权为0
add(0,i,0);
}
cnt[0]=1;
SPFA(0);
if(flag){ //图中存在负环
puts("-1");
return 0;
}
for(int i=1;i<=n;i++){
int len=edge[i].size();
for(int j=0;j<len;j++){
create_new(i,edge[i][j],w[i][j]); //建新图
}
}
for(int i=1;i<=n;i++){
Dijkstra(i);
for(int j=1;j<=n;j++){
if(dis[i][j]>=4000000000000000000) //inf
dis[i][j]=1e9;
else{
dis[i][j]=dis[i][j]-h[i]+h[j]; //最短路长度复原，最终dis[i][j]即为原图中i到j的最短路
}
}
}
return 0;
}
