【转载】状压dp入门指引 by Xx_queue

原文链接

目录

• • -1.前言
  • 0.概述
• 1.位运算(建议初学者认真研究,这是基础)
• 2.常用的计算方法:(建议认真食用,灵活运用)
  • • 重点:用二进制表示的集合的基本运算(有待补充)
    • 其他运算
• 3.状态压缩
• 4.状压DP(其实就是状压+DP)
• 5.与枚举子集有关的状压DP

-1.前言

这几天学习了一下状压DP(毕竟CSP初赛就是状压挂掉了),现在也是时候总结一下学习成果,庆祝自己大概学会了状压DP?(雾;

0.概述

这次蒟蒻Xx_queue要和大家一起来学习DP中的很重要的一类:状压DP(状态压缩动态规划);

状压DP，是用二进制来描述状态的一种DP,适用于数据范围比较小的情形,状压DP就是状压+DP;

举个例子:关灯问题:

---

题目:

现有n盏灯，以及m个按钮。每个按钮可以同时控制这n盏灯——按下了第i个按钮，对于所有的灯都有一个效果。按下i按钮对于第j盏灯，是下面3中效果之一：如果a[i][j]为1，那么当这盏灯开了的时候，把它关上，否则不管；如果为-1的话，如果这盏灯是关的，那么把它打开，否则也不管；如果是0，无论这灯是否开，都不管。

现在这些灯都是开的，给出所有开关对所有灯的控制效果，求问最少要按几下按钮才能全部关掉。

---

先不管题目说的啥,我们就只考虑怎么状压,也就是怎么用二进制来表示状态:

假设n=5,第1,4,5盏灯亮,第2,3盏灯灭,我们就可以考虑利用一个二进制串:11001来表示这个状态:

灯	5	4	3	2	1
状态	1	1	0	0	1
(0表示灭,1表示亮)

是不是很清晰?

所以这个二进制串:11001

就可以表示这5盏灯目前的状态;(题目后面会讲到)

1.位运算(建议初学者认真研究,这是基础)

相信考过CSP的大家都会

几种位运算的方法如下所示(制表不易):

名称	符号	运算法则	举例
按位与	a & b	相同为1,不同为0	00101&11100=00100
按位或	a | b	有1为1,无1为0	00101|11100=11101
按位异或	a ^ b	相同为0,不同为1	00101^11100=11001
按位取反	~a	是1为0,是0为1	~00101=11010
左移	a << b	把对应的二进制数左移b位	00101<<2=0010100
右移	a >> b	把对应的二进制数右移b位	00101>>1=0010

大概就这样吧......(或者你可以百度百科一下)

2.常用的计算方法:(建议认真食用,灵活运用)

状压DP要求掌握一定的二进制计算方法,所以大家一定要运用熟练(主要还是要多做题)

建议一边看一边手玩一下,举几个例子更便于理解

重点:用二进制表示的集合的基本运算(有待补充)

运算	计算方法
集合相交	x=a&b
集合相并	x=a|b
枚举子集	for(int x=sta;x;x=((x-1)&sta))

其他运算

可以看看这个图片(来自网络):

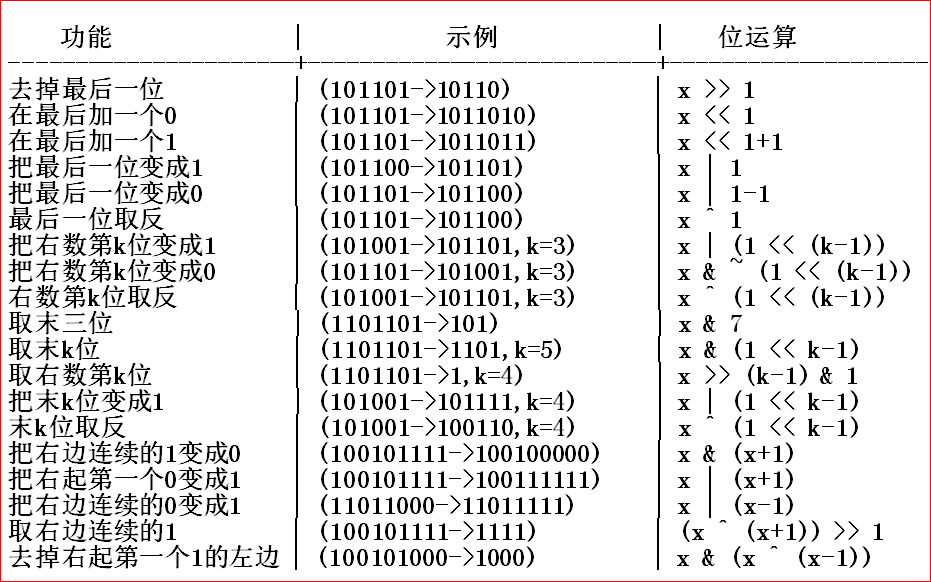
也可以看看这些密密麻麻的文字(我是真不想看)(来自网络):

---

取出x的第i位:\(y=(x>>(i-1))\&1\);

将x第i位取反:$x $ ^ $ = 1<<(i-1)$;

将x第i位变为1:\(x|= 1<<(i-1)\);

将x第i位变为0:\(x\&= ~(1<<(i-1))\);

将x最靠右的1变成0:\(x= x\&(x-1)\);

取出x最靠右的1:\(y=x\&(-x)\);(lowbit函数)

把最靠右的0变成1:\(x|=x+1\)

判断是否有两个连续的1:\(if(x\&(x<<1))\) \(cout<<"YES";\)

判断是否有𝑛个连续的1:\(if(x\&(x<<1)\&\&x\&(x<<2)...\&\&x\&(x<<n-1))\)

---

(写于2019.10.24上午)

(分割线)

---

(2019.10.24晚上)蒟蒻又双叒叕来填坑了(话说之前还有好多坑没填)

3.状态压缩

二进制状态压缩,是指将一个长度为m的bool数组(也就是只有0,1两种状态)用一个m位二进制整数表示并储存的方法.(摘自李煜东《算法竞赛进阶指南》,括号内容为自行备注)

概述中已经说过状态压缩是何物了,这里就不再赘述;

那么我们来详细研究概述中的例子:关灯问题

关灯问题

题目传送门

分析:

---

暴力dfs搜索?据说会爆栈

考虑状态压缩,之前就说过了,可以把灯的开关视作1和0,则用一串01串(二进制)表示这一串灯的一个总的状态,不知大家有没有理解??

因为这个01串是二进制的,所以它们所对应的十进制数最大不会超过(2<<10)-1=1023(n<=10);

也就是最多只有1023种状态,所以当然可行;

现在大概理解状态压缩为什么只适用于小范围的数据了吧,因为如果这个二进制数的长度超过64,unsigned long long都存不下啦!!!

那么这题可以用广搜直接暴力搞,利用之前的计算方法,开灯(1)就是把对应的那一位0变成1:\(x|= 1<<(i-1)\),如果本身就是1的话当然也没有任何影响;

同理,关灯(-1)的话就是把对应的那一位1变成0:\(x\&= ~(1<<(i-1))\),当然如果本身是0,也没有影响啦!如果控制的操作是0,那就不管呗;

所以就很简单啊,直接广搜就可以啦;

---

详细请见代码;

AC代码:

#include <bits/stdc++.h>
#define N (10000+5)
using namespace std;
int n,m,ans[N],flag;
int vis[N],light[1000][1000];
queue <int>q;
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++){
		for(int j=1;j<=n;j++){
			scanf("%d",&light[i][j]);
		}
	}
	int Begin=0;
	for(int i=1;i<=n;i++) Begin=Begin<<1|1;//初始化是全部为开灯(111111111)
	q.push(Begin);
	vis[Begin]=1;
	while(!q.empty()){//广搜
		int last,now=q.front();
		last=now;
		q.pop();
		for(int i=1;i<=m;i++){
			now=last;
			for(int j=1;j<=n;j++){
				if(light[i][j]==1){//如果当前控制的操作是1
					now=now&(~(1<<(j-1)));//关灯(把第j位1变成0)
				}
				else if(light[i][j]==-1){//如果当前控制的操作是0
					now=now|(1<<(j-1));//开灯(把第j位0变成1)
				}
			}
			if(!vis[now]){
				vis[now]=1;
				ans[now]=ans[last]+1;
				if(now==0) {flag=1;printf("%d",ans[now]);break;}
				q.push(now);
			}
		}
	}
	if(!flag)printf("-1");
	return 0;
}

4.状压DP(其实就是状压+DP)

先来看一道模板题:玉米田(这个模板题十分重要,到后面你就知道它为什么这么重要了)

[USACO06NOV]玉米田Corn Fields

题目传送门

题目翻译:(摘自洛谷)

农场主John新买了一块长方形的新牧场，这块牧场被划分成M行N列(1 ≤ M ≤ 12; 1 ≤ N ≤ 12)，每一格都是一块正方形的土地。John打算在牧场上的某几格里种上美味的草，供他的奶牛们享用。

遗憾的是，有些土地相当贫瘠，不能用来种草。并且，奶牛们喜欢独占一块草地的感觉，于是John不会选择两块相邻的土地，也就是说，没有哪两块草地有公共边。

John想知道，如果不考虑草地的总块数，那么，一共有多少种种植方案可供他选择？（当然，把新牧场完全荒废也是一种方案）
输入格式

第一行：两个整数M和N，用空格隔开。

第2到第M+1行：每行包含N个用空格隔开的整数，描述了每块土地的状态。第i+1行描述了第i行的土地，所有整数均为0或1，是1的话，表示这块土地足够肥沃，0则表示这块土地不适合种草。
输出格式

一个整数，即牧场分配总方案数除以100,000,000的余数。

输入输出样例

输入 1

2 3
1 1 1
0 1 0

输出 1

9

分析:

---

先看数据范围:M,N<=12,嗯,肯定是状压DP了;

考虑如何状压?直接用1表示种了草,0表示没有(每一行都有这么一些状态)

所以每一行的状态就可以描述出来了,每行状态总数为(1<<12)-1=4095种,空间是没有问题的;

问题是怎么判断状态合不合法?

---

三连问:

1.同一行有没有相邻的土地种植了草?

直接左移一位(或右移一位)与原状态求交集,为空集则合法;

2.有没有草种在贫瘠的土地上?

把原土地的状态表示出来,0为贫瘠,还是分每行来表示;

将该状态与土地的贫富状态求一下交集,如果等于原状态(即原状态是土地状态的子集),则合法;

3.上下两行之间有两格土地连在了一起怎么办?

这个在DP转移的时候判一下,枚举一下上一行的状态(设为k,当前状态设为j),与第1个小问相同,如果k与j交集为空集,则合法,可由k转移过来;

---

所以是不是比较清楚了,建议大家边看代码边思考这三个问题,结合集合的基本运算,相信大家一定可以看懂!

AC代码:

#include <bits/stdc++.h>
#define N (12+2)
using namespace std;
int n,m,mod=1e8;
int mapp[N][N],dp[N][1<<N],f[N];
bool rightt[1<<N];
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			scanf("%d",&mapp[i][j]);
			f[i]=(f[i]<<1)|mapp[i][j];//存入每一行土地的状态
		}
	}
	dp[0][0]=1;
	int siz=1<<m;
	for(int i=0;i<siz;i++){
		if(!((i<<1)&i)&&!((i>>1)&i)) rightt[i]=true;//判断状态是否合法(问题1)
	}
	for(int i=1;i<=n;i++){
		for(int j=0;j<siz;j++){
			if(rightt[j]&&(f[i]&j)==j){//判断状态是否合法(问题2)
				for(int k=0;k<siz;k++){
					if(!(k&j)) dp[i][j]=(dp[i][j]+dp[i-1][k])%mod;//判断状态是否合法再转移(问题3)
				}
			}
		}
	}
	int ans=0;
	for(int i=0;i<siz;i++){
		ans=(ans+dp[n][i])%mod;//统计答案
	}
	printf("%d",ans);
	return 0;
}

有木有对于状压DP豁然开朗?

---

(写于2019.10.25晚上)

我们再举一个栗子呗:[SCOI2005]互不侵犯

[SCOI2005]互不侵犯

题目传送门

题目描述

在N×N的棋盘里面放K个国王，使他们互不攻击，共有多少种摆放方案。国王能攻击到它上下左右，以及左上左下右上右下八个方向上附近的各一个格子，共8个格子。

输入格式

只有一行，包含两个数N，K （ 1 <=N <=9, 0 <= K <= N * N）

输入格式

所得的方案数

输入输出样例

输入 1

3 2

输出 1

16

---

分析:

这个题目不就是玉米田稍微加强了一下子?

有没有很容易想到解题方法??

只不过这里的国王是四面八方总共八个格子都不能摆放其他国王,也就只是限制不同而已;

所以判断上下两行是否有冲突时就多了一点点,我们只需要要:左移求交集,直接求交集,右移求交集来看是否合法,有交集则为不合法,这应该很好想吧?

还有,由于第一行的特殊性(它上面没有限制),所以我们可以事先把第一行预处理出来;

具体如何实现状态的转移?这里只简单说说如何设计状态:

开三个维度来储存DP的状态(因为题目里面有两个要求:n行,以及固定了要求摆放的棋子个数,剩下一个维度是状压的状态,这也是基本套路);

\(dp[i][j][k]\)表示第i行,这一行国王摆放的状态为j,已经摆放了k个国王;

所以这里还需要先把每种国王摆放状态的国王个数预处理出来(下面的程序里使用state数组来存);

注意事项:开long long!!

好了不多说了,上代码!(有木有与玉米田的做题套路十分雷同??)

---

AC代码:(ch数组貌似没什么用,请忽略)

#include <bits/stdc++.h>
#define N 10
using namespace std;
int n,K;
int ch[N],state[N];
long long dp[N][1<<N][100];
bool rightt[1<<N];
int main(){
	scanf("%d%d",&n,&K);
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			ch[i]=(ch[i]<<1)|1;//没用
		}
	}
	int siz=(1<<n);
	for(int i=0;i<siz;i++){
		if(!((i<<1)&i)&&!((i>>1)&i)){//判断状态是否合法
			rightt[i]=1;
			int temp=i;
			while(temp){
				if(temp&1) state[i]++;//预处理每个状态需要的国王数
				temp>>=1;
			}
		}
	}
	for(int i=0;i<siz;i++){
		if(rightt[i]) dp[1][i][state[i]]=1;//预处理第一行
	}
	for(int i=2;i<=n;i++){
		for(int j=0;j<siz;j++){
			if(!rightt[j]) continue;//不合法,去掉
			for(int k=0;k<siz;k++){
				if(!rightt[k]) continue;
				if((j&(k<<1))||(j&k)||(j&(k>>1))) continue;//不合法,continue
				for(int l=K;l>=state[j];l--){
					dp[i][j][l]+=dp[i-1][k][l-state[j]];//转移,加上
				}
			}
		}
	}
	long long ans=0;
	for(int i=0;i<siz;i++){
		ans+=dp[n][i][K];//统计答案
	}
	printf("%lld",ans);
	return 0;
}

---

Congratulations!恭喜你差不多学会了状压DP,下面我将会用一到例题讲一讲状压DP的一个小小的优化策略;

请看:炮兵阵地;

[NOI2001]炮兵阵地

题目传送门

题目描述

司令部的将军们打算在NM的网格地图上部署他们的炮兵部队。一个NM的地图由N行M列组成，地图的每一格可能是山地（用“H” 表示），也可能是平原（用“P”表示），如下图。在每一格平原地形上最多可以布置一支炮兵部队（山地上不能够部署炮兵部队）；一支炮兵部队在地图上的攻击范围如图中黑色区域所示：

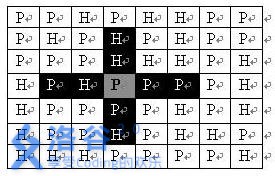
如果在地图中的灰色所标识的平原上部署一支炮兵部队，则图中的黑色的网格表示它能够攻击到的区域：沿横向左右各两格，沿纵向上下各两格。图上其它白色网格均攻击不到。从图上可见炮兵的攻击范围不受地形的影响。 现在，将军们规划如何部署炮兵部队，在防止误伤的前提下（保证任何两支炮兵部队之间不能互相攻击，即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内），在整个地图区域内最多能够摆放多少我军的炮兵部队。

输入格式

第一行包含两个由空格分割开的正整数，分别表示N和M；

接下来的N行，每一行含有连续的M个字符（‘P’或者‘H’），中间没有空格。按顺序表示地图中每一行的数据。N≤100；M≤10。

输出格式

仅一行，包含一个整数K，表示最多能摆放的炮兵部队的数量。

输入输出样例

输入 1

5 4
PHPP
PPHH
PPPP
PHPP
PHHP

输出 #1

6

---

分析:

通过读题,我们发现这道题目和玉米田很像(怎么又是玉米田啊喂!都说了玉米田很重要的啦)

没错,H地形不能放置炮兵就和玉米田那道题目里面处理贫瘠土地的方式一模一样,这里不再赘述;

关键是这里每一行对其下方两行都有较大的影响,所以这里我们不能偷懒,必须要多设计一维状态表示当前一行的上一行的状态是什么;

设dp[i][j][k]表示第i行,当前行状态为j,上一行状态为k;

来看看题目数据范围,m<=10?

每一行有1<<(10-1)种状态,也就是1023种,不多不多;

What?n<=100?

dp[101][1024][1024],不会MLE炸掉就奇了怪了;

而且就算不会炸,那也很容易超时好吧;

所以要怎么办呢?

这里不妨用一个简单但是非常实用的优化:把合法的状态开个数组存起来就OK了!

震惊.jpg

在这道题目里面,合法的状态判断方法为:

for(int i=0;i<siz;i++){
	if(i&(i>>2)||i&(i>>1)||i&(i<<1)||i&(i<<2)) continue;//不合法就continue
	int temp=i;
	state[++cnt]=i;//合法状态++,并储存(此处用数组state存储)
	while(temp){
		if(temp&1) need[cnt]++//预处理出每种状态need的炮兵个数;
		temp>>=1;
	}
}

应该比较好懂吧;

这时候我们只要枚举cnt就可以了枚举合法状态了;

是不是很easy??

注意这道题目因为第一行和第二行都比较特殊,所以都需要先预处理出来;

当然你也可以使用滚动数组大法(详见洛谷题解,里面肯定有)

那么其余的细节也就不再多说,仔细研究代码就很好懂了;

---

AC代码:

#include <bits/stdc++.h>
#define N 105
#define M 11
using namespace std;
int n,m,cnt;
int mapp[N],state[1<<M],need[1<<M];
int dp[N][N][N];
char a;
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			scanf("%1s",&a);
			if(a=='P') mapp[i]=(mapp[i]<<1)|1;
			else mapp[i]<<=1;
		}
	}
	int siz=(1<<m);
	for(int i=0;i<siz;i++){
		if(i&(i>>2)||i&(i>>1)||i&(i<<1)||i&(i<<2)) continue;
		int temp=i;
		state[++cnt]=i;
		while(temp){
			if(temp&1) need[cnt]++;
			temp>>=1;
		}
	}
	for(int i=1;i<=cnt;i++){//预处理第1行,枚举这一行的状态(state[i]),上一行状态为0,不用枚举
		int now=state[i];
		if((now&mapp[1])!=now) continue;
		dp[1][i][0]=need[i];
	}
	for(int i=1;i<=cnt;i++){//预处理第2行,枚举这一行的状态(state[i])
		int now1=state[i];
		if((now1&mapp[1])!=now1) continue;
		for(int j=1;j<=cnt;j++){//枚举上一行的状态(state[j]),上2行的状态为0
			int now2=state[j];
			if((now2&mapp[2])!=now2||now2&now1) continue;
			dp[2][j][i]=max(dp[2][j][i],dp[1][i][0]+need[j]);//转移(应该看得懂吧)
		}
	}
	for(int i=3;i<=n;i++){//第3~n行(i为第几行)
		for(int j=1;j<=cnt;j++){//枚举第i行的状态(state[j])
			int now1=state[j];
			if((now1&mapp[i-2])!=now1) continue;
			for(int k=1;k<=cnt;k++){//枚举第i-1行的状态(state[k])
				int now2=state[k];
				if((now2&mapp[i-1])!=now2||now2&now1) continue;
				for(int l=1;l<=cnt;l++){//枚举第i-2行的状态(state[l])
					int now3=state[l];
					if((now3&mapp[i])!=now3||now3&now2||now3&now1) continue;
					dp[i][l][k]=max(dp[i][l][k],dp[i-1][k][j]+need[l]);//转移(同预处理第二行的方法)
				}
			}
		}
	}
	int ans=0;
	for(int i=1;i<=cnt;i++){//统计答案
		for(int j=1;j<=cnt;j++){
			ans=max(ans,dp[n][j][i]);
		}
	}
	printf("%d",ans);
	return 0;
}

怎么样,学到了吧;

当然你也可以使用滚动数组优化空间(不保证不会T,没有写过,请研究洛谷题解)

---

接下来我们来一道神仙题吧!!

[HNOI2012]集合选数

题目传送门

---

题目描述

《集合论与图论》这门课程有一道作业题，要求同学们求出{1, 2, 3, 4, 5}的所有满足以 下条件的子集：若 x 在该子集中，则 2x 和 3x 不能在该子集中。

同学们不喜欢这种具有枚举性 质的题目，于是把它变成了以下问题：对于任意一个正整数 n<=100000，如何求出{1, 2,..., n} 的满足上述约束条件的子集的个数（只需输出对 1,000,000,001 取模的结果），现在这个问题就 交给你了。

输入格式
只有一行，其中有一个正整数 n，30%的数据满足 n<=20。

输出格式
仅包含一个正整数，表示{1, 2,..., n}有多少个满足上述约束条件 的子集。

输入输出样例

输入 1
4

输出 1
8

样例解释

有8 个集合满足要求，分别是空集，{1}，{1，4}，{2}，{2，3}，{3}，{3，4}，{4}。

---

先给大家10分钟的时间想一想看看有没有一点点思路??

(可能你正在看数据范围,然后不禁感叹:这是状压DP???我才不信!)

---

分析:

这是一道神仙构造题;如果我跟你说它是玉米田,你可能一定不会相信;

但它就和玉米田这道题是一样的,不信?你且听我细细道来:

首先我们看看题目中的描述:x不能与2x,3x在同一个集合里面;(也就是说4x,5x之后的都随便你取不取)

想想玉米田,相邻的土地不能都种植;可以考虑把x与2x,3x划分到相邻的土地上,于是可以构造出矩阵:(其实我也看了题解的啦)

1	2	3	4	...
x	2x	4x	8x	...
3x	6x	12x	24x	...
9x	18x	36x	...	...
...	...	...	...	...

这样就成了矩阵里面相邻的数不能选取的[玉米田]问题啦!

但是1个矩形肯定没有涵盖所有的数;

怎么办?

对每个即不是2的倍数又不是3的倍数的数作为x

构造矩形,然后根据乘法原理,答案就是各个矩形求出来的结果相乘。

剩下的你就应该知道怎么做了吧......(具体细节请研究代码)

(构造矩形的函数尽量自己写出来)

这里就不再赘述,因为就是玉米田问题;

讲几个注意事项:
1.这个题非常容易TLE,千万不要用memset,否则会T飞去;

2.开long long,记得取mod

3.加一堆玄学优化就能过了(例如位运算,register,inline等)(或者开O2)
不然你真的会T到想死的!

4.再不行的话就避免重复计算,用变量存储siz=1<<(......);(见代码)
不然每次判断都要计算一次耗时量巨大

---

AC代码:

#include <bits/stdc++.h>
#define N (100000+5)
#define int long long
using namespace std;
int n,mod=1e9+1,ans=1;
long long a[50][50];
bool vis[N];
long long dp[50][1<<20];
bool rightt[1<<20];
int cnti=0,cntj[50];
inline void create(int x){//构造矩形
	cnti=0;
	for(register int i=x;i<=n;i*=3){
		++cnti;cntj[cnti]=0;
		for(register int j=1;i*j<=n;j<<=1){
			++cntj[cnti];
			a[cnti][cntj[cnti]]=i*j;
			vis[i*j]=1;
		}
	}
}
inline int cont(){//计算每个矩形的符合条件的子集数
	int ss=1<<cntj[1];//开个变量储存一下
	for(register int i=0;i<ss;++i){
		dp[1][i]=rightt[i];
	}
	for(register int i=2;i<=cnti;++i){//同玉米田(只是没有贫瘠的土地QWQ)
		int siz=(1<<cntj[i]);//同ss
		for(register int j=0;j<siz;++j){
			if(!rightt[j]) continue;
			dp[i][j]=0;
			int sizs=(1<<cntj[i-1]);//同siz
			for(register int k=0;k<sizs;++k){
				if(rightt[k]&&!(k&j))dp[i][j]=(dp[i][j]+dp[i-1][k])%mod;
			}
		}
	}
	int res=0,siz=1<<cntj[cnti];//没必要解释了吧
	for(register int i=0;i<siz;++i){
		res=(res%mod+dp[cnti][i]%mod)%mod;
	}
	return res;
}
signed main(){
	scanf("%lld",&n);
	int siz=1<<17;
	for(register int i=0;i<siz;++i){
		if(!(i&(i<<1))) rightt[i]=true;//合法状态
	}
	for(register int i=1;i<=n;++i){
		if(!vis[i]) create(i),ans=(ans%mod*cont()%mod)%mod;//没有访问过(也就是既不是2也不是3的倍数的数)就create;
	}
	printf("%lld",ans);
	return 0;
}

---

5.与枚举子集有关的状压DP

[NOIP2017TG] 宝藏

讲解传送门

---

相信你的状压DP已经入门啦!!加油,再接再厉;

希望我能帮到你一点点......