[新手向] 动态规划引入
[新手向] 动态规划引入
被迫营业qwq，写一篇新手向的动态规划blog
小场景（可跳过）：
多年后，几个曾经学过\(OI\)但是比较菜的小伙伴，有缘能聚在一起交流
\(A\): 我还记得当初学\(OI\)的时候，一开始我雄心壮志，后面学到递归和搜索，就给我整不会了，研究了好久才搞明白；后面学到动态规划，直接给我劝退了
\(B\): 确实，动态规划给我人整麻了，笑死，就没看懂过
\(C\): 真的，我做dp的题，费了老大劲才看懂题解，结果自己上手啥也不会
\(A\): 式子推不出来啊呜呜呜
\(B\): 状态都设计不出来，还推式子
\(A B C\): 唉！动态规划怎么这么难！
（备注：灵感来源于现实生活）
一、何为动态规划
1. 动态规划的定义
- 动态规划（英语：Dynamic programming，简称DP）是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的，通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。
- 动态规划常常适用于有重叠子问题和最优子结构（英语：Optimal substructure）性质的问题，动态规划方法所耗时间往往远少于朴素解法。 ——摘自维基百科
2. 由递归到动态规划
仔细琢磨一下动态规划的定义，这玩意儿怎么感觉和递归这么像捏？？
你瞧，动态规划，是把原问题分解为相对简单的子问题的方式求解复杂问题的方法。
递归不就是这样吗？
对于我们经典的爬楼梯问题：有\(n\)级台阶，你每次可以爬1级或者2级，求最终爬到第\(n\)级有多少中不同的爬楼梯方案。我们在C语言课堂中用的是递归来解决这个问题的。解题思路大概就是：
(1)假设我现在在第\(n\)级，我是怎么到这里来的？要么就是从\(n-1\)级台阶走1级到第\(n\)级，要么就是从\(n-2\)级台阶走2级到第\(n\)级；
(2)那么问题就转化成，我是怎么走到第\(n-1\)级台阶和第\(n-2\)级台阶的了，是不是就可以套用第(1)步的方法来求解走到第\(n-1\)级台阶和第\(n-2\)级台阶这两个小问题；
这就是递归，把大问题分成相似的小问题，小问题又可以再分，代码段示例如下（注意递归边界的处理）
int f(int x){
if(x==1) return 1;//我当前处于第1级台阶，我有几种走法？1种
if(x==2) return 2;//我当前处于第2级台阶，我有几种走法？2种
return f(x-1)+f(x-2);//我当前处于第x级台阶，我怎么走来的？从x-1走1级+从x-2走2级
}
但是在上课的时候，应该有同学做过实验，就是输入\(n=100\)或者更大，程序就像陷入了死循环一样，根本出不来答案？这是怎么一回事呢？
其实不是它跑不出来答案，而是计算量实在是太大太大了。我们把式子展开一下：
\(f(n)=f(n-1)+f(n-2)=[f(n-2)+f(n-3)]+[f(n-3)+f(n-4)]=...\)
会发现，（不严谨的说法）计算量从2变到4，再变到8，每次都翻倍了，这样下去，\(n\)如果稍微大一点点，程序的计算量就贼大贼大，就要跑很久很久。这对于追求速度的我们，是完全不ok的
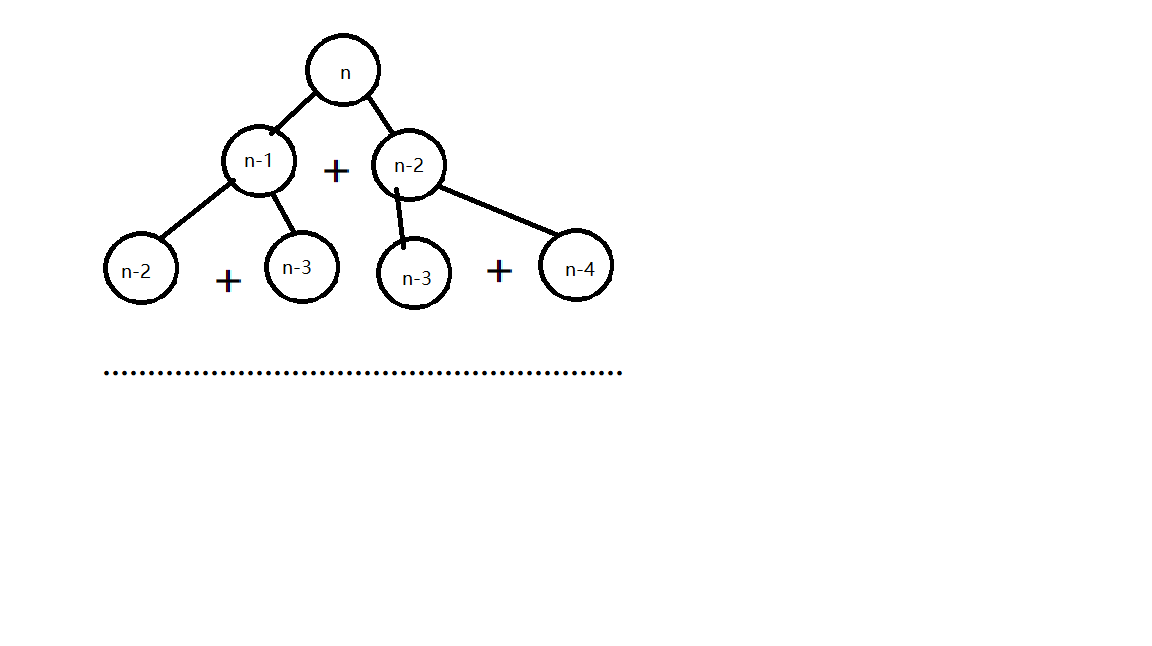
细心的同学可能会发现，我们其实重复算了很多东西，比如\(f(n-2)\)，我们算了两次，\(f(n-3)\)，我们算了3次......那么有没有一种可能，比如说，我们在第一次把\(f(n-2)\)算出来之后，把它的值保存下来，下次再遇到\(f(n-2)\)的时候，直接调用已经保存的值，就不用重复计算了
诶，那么我们的计算过程似乎变成了这样
是不是大大缩减了计算过程？
代码段如下：
int dp[100005];//dp[x]表示走到第x级台阶的方法数
dp[1]=1,dp[2]=2;//在第1级和第2级的走法数
int f(int x){
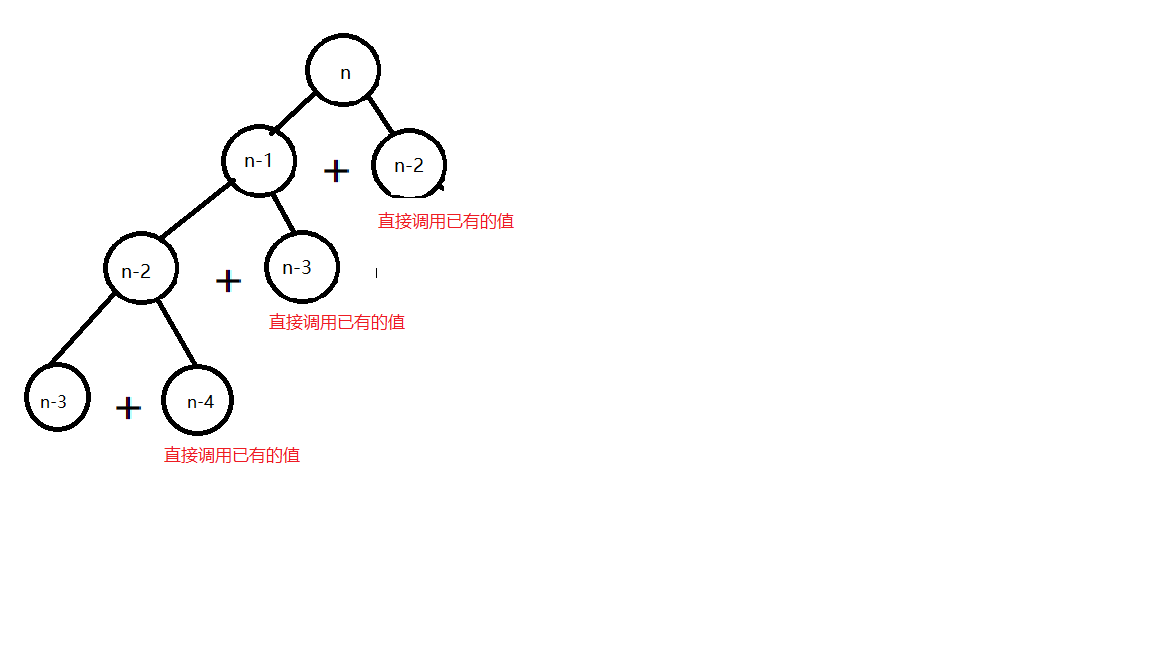
if(dp[x]!=0) return dp[x];//如果曾经走到过第x级台阶并储存下来过它的值，直接调用
dp[x]=f(x-1)+f(x-2);//我当前处于第x级台阶，我怎么走来的？从x-1走1级+从x-2走2级，用dp[x]存一下
return dp[x];
}
这样你可以试一下，别说是\(n=100\)了，就是\(n=100000\)，也能跑出结果
这就是动态规划，以空间换时间，耗费一定的空间把曾经算过的结果存起来，要用的时候直接用，不用再算。
3. 非递归版本的动态规划
上面那种是递归版本的动态规划，更一般递归形式的动态规划我们常把它叫做记忆化搜索，其实是深度优先搜索算法（dfs）的记忆化，更多内容请自行查阅资料。
有人说，可恶我递归学的不好，不想用递归怎么办。别慌，非递归形式的动态规划是存在滴
我们递归形式的动态规划，实际上计算顺序是从\(f(n)\)倒推回去；
只要我们换一个推的顺序，即最开始已知\(f(1)\)和\(f(2)\)，\(f(3)=f(1)+f(2)\)，.......按顺序往后推，它就变成了递推形式的动态规划，也就是广大OIer更喜闻乐见的动态规划的代码实现形式
代码段如下：
int dp[100005];
dp[1]=1,dp[2]=2;
for(int i=3;i<=n;i++){
dp[i]=dp[i-1]+dp[i-2];
}
最后\(dp[n]\)就是所求结果，这玩意儿其实就是个斐波那契数列
4. 一些动态规划的题目
贴个题单在这里，很多题目相对来说有一定难度
有个名叫数字三角形的题目一定要看一看，这个是真正的动态规划入门题目，斐波那契数列属于不入流的；里面也有我们接下来要讲到的背包问题
5. 求解动态规划问题的一般步骤与思路
相关术语请查询百度百科或其他资料
通过分析大量的可以利用动态规划算法的题目，我们可以总结一下，什么样的题目可以用动态规划算法来解决
-
(1) 具有最优子结构性质
如果子问题的最优解正好可以推出更大问题的最优解，官方一点的说，如果问题的最优解所包含的子问题的解也是最优的，我们就称该问题具有最优子结构性质（即满足最优化原理）。动态规划的状态转移方程一般从这里入手推起
-
(2) 无后效性
子问题的解一旦被确定，就不再被影响，不会被改变，后续决策不会对已经求得的子问题的最优解产生影响
-
(3) 子问题的重叠性质
子问题重叠性质是指在用递归算法自顶向下对问题进行求解时，每次产生的子问题并不总是新问题，有些子问题会被重复计算多次。就像之前的例子中，\(f(n-2)\)被算了多次，可以存起来，之后再遇到时，直接调用。
如何求解动态规划问题？
常用的解题思路为：
- (1) 确定子问题
- (2) 确定状态
- (3) 推状态转移方程
- (4) 确定边界
- (5) 确定实现方式
- (6) (非必要)优化
注意，接下来讨论的问题，需要对于动态规划有一定的了解才行。0基础的，先去练练级再来。
在学习的时候，一定要多多查阅其他的资料，反复研究更多的资料，才会有所长进
二、动态规划的经典问题——背包问题
1. 什么是背包问题
-
背包问题（英语：Knapsack problem）是一种组合优化的NP完全问题。问题可以描述为：给定一组物品，每种物品都有自己的重量和价格，在限定的总重量内，我们如何选择，才能使得物品的总价格最高。问题的名称来源于如何选择最合适的物品放置于给定背包中，背包的空间有限，但我们需要最大化背包内所装物品的价值。背包问题通常出现在资源分配中，决策者必须分别从一组不可分割的项目或任务中进行选择，而这些项目又有时间或预算的限制。
——摘自维基百科
2. 01背包
举一个非常经典的例子
1° [NOIP2005 普及组] 采药
题目描述
辰辰是个天资聪颖的孩子，他的梦想是成为世界上最伟大的医师。为此，他想拜附近最有威望的医师为师。医师为了判断他的资质，给他出了一个难题。医师把他带到一个到处都是草药的山洞里对他说：“孩子，这个山洞里有一些不同的草药，采每一株都需要一些时间，每一株也有它自身的价值。我会给你一段时间，在这段时间里，你可以采到一些草药。如果你是一个聪明的孩子，你应该可以让采到的草药的总价值最大。”
如果你是辰辰，你能完成这个任务吗？
输入格式
第一行有 \(2\) 个整数 \(T\)（\(1 \le T \le 1000\)）和 \(M\)（\(1 \le M \le 100\)），用一个空格隔开，\(T\) 代表总共能够用来采药的时间，\(M\) 代表山洞里的草药的数目。
接下来的 \(M\) 行每行包括两个在 \(1\) 到 \(100\) 之间（包括 \(1\) 和 \(100\)）的整数，分别表示采摘某株草药的时间和这株草药的价值。
输出格式
输出在规定的时间内可以采到的草药的最大总价值。
样例 #1
样例输入 #1
70 3
71 100
69 1
1 2
样例输出 #1
3
提示
【数据范围】
- 对于 \(30\%\) 的数据，\(M \le 10\)；
- 对于全部的数据，\(M \le 100\)。
【题目来源】
NOIP 2005 普及组第三题
上述问题是典型的01背包问题(01 knapsack problem)。01背包问题的基本模型是：
-
一共有\(N\)件物品，第\(i\)（\(i\)从1开始）件物品的重量为\(w[i]\)，价值为\(v[i]\)。
在总重量不超过背包承载上限\(W\)的情况下，能够装入背包的最大价值是多少？
我们定义状态\(dp [i] [j]\)意义如下
dp[i][j]表示把前i个物品装入限重为j的背包中，可以获得的最大价值
那么现在对于第\(i\)件物品，我们来做决策：
-
(1) 第\(i\)件物品丢掉，不装进来，那么就有
dp[i][j]=dp[i-1][j];//第i件物品丢掉 -
(2) 第\(i\)件物品装进来，注意，必须要装得下才行，不然只能丢掉
耗费\(w[i]\)的重量，但使得总价值增加\(v[i]\)
dp[i][j]=dp[i-1][j-w[i]]+v[i];//装入第i件物品，要保证j-w[i]>=0!即必须要装得下那么怎么做决策呢？两者之间，选择最大！即：
dp[i][j]=max(dp[i−1][j], dp[i−1][j−w[i]]+v[i]);//j-w[i]>=0
上述过程就是关于01背包问题状态转移方程的推导
2° 一个优化——滚动数组
有趣的是，对于上述01背包的状态转移方程，我们还可以做进一步的优化
从上述状态转移方程不难发现，\(dp [i] [j]\)的值仅与\(dp[i-1] [ 0 ,..., j-1 ]\)有关，于是我们可以采用喜闻乐见的滚动数组方法，对空间进行优化
一般的滚动数组优化采取的是%2的方式进行优化，伪代码如下：
for(int i=1;i<=n;i++){
...
dp[i%2][j]=max(dp[(i-1)%2][j],dp[(i-1)%2][j-w[i]]+v[i]);
...
}
对于01背包我们甚至可以把它优化到一维数组，但是需要注意的是，为了防止之前有用的值被覆盖掉，循环的时候j只能够反向枚举
代码段如下：
for(int i=1;i<=n;i++){
for(int j=W;j>=w[i];j--){
dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
}
}
3. 完全背包
上述01背包问题，每种物品只有一个，可是假设每种物品有无限多个呢，怎么办！！！
这就是接下来要讲到的完全背包问题
1° 经典模型
完全背包（unbounded knapsack problem）与01背包不同就是每种物品可以有无限多个：一共有\(N\)种物品，每种物品有无限多个，第\(i\)（\(i\)从1开始）种物品的重量为\(w[i]\)，价值为\(v[i]\)。在总重量不超过背包承载上限\(W\)的情况下，能够装入背包的最大价值是多少？
类比01背包，我们还是可以设计状态\(dp [i] [j]\)意义如下：
dp[i][j]表示把前i个物品装入限重为j的背包中，可以获得的最大价值
那么同样的，现在对于第\(i\)件物品，我们来做决策：
-
(1) 第\(i\)件物品丢掉，不装进来，与01背包相同，那么就有
dp[i][j]=dp[i-1][j];//第i件物品丢掉 -
(2) 第\(i\)件物品装进来，此时和01背包就有差别了
现在每种物品有无限多个，那么等于说，在装入了第\(i\)个物品后，还可以再继续装入第\(i\)个物品，同样注意，必须要装得下才行，不然只能丢掉，即：
dp[i][j]=dp[i][j-w[i]]+v[i];//装入第i件物品，要保证j-w[i]>=0!即必须要装得下那么怎么做决策呢？老规矩，两者之间，选择最大！即：
dp[i][j]=max(dp[i−1][j], dp[i][j−w[i]]+v[i]);//j-w[i]>=0
上述过程就是关于完全背包问题状态转移方程的推导
2° 滚动数组优化
对于完全背包，也可以用滚动数组优化至一维，但是在这里与01背包不同，它的\(j\)必须要正向枚举
具体原理可以参考
代码段如下：
for(int i=1;i<=n;i++){
for(int j=w[i];j<=W;j++){
dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
}
}
4. 更深入地研究
如果你对背包问题很感兴趣，只了解这些肯定是不够的，推荐经典的背包问题九讲
