【学习笔记】权值线段树
一. 权值线段树
权值线段树即一种线段树，以序列的数值为下标。节点里所统计的值为节点所对应的区间 \([l,r]\) 中，\([l,r]\) 这个值域中所有数的出现次数。
举个例子，有一个长度为 \(10\) 的序列 \(\{1,5,2,3,4,1,3,4,4,4\}\)。
那么统计每个数出现的次数。易知 \(1\) 出现了 \(2\) 次，\(2\) 出现了 \(1\) 次，\(3\) 出现了 \(2\) 次，\(4\)出现了 \(4\)次，\(5\) 出现了 \(1\) 次。
那么我们可以建出一棵这样的权值线段树：
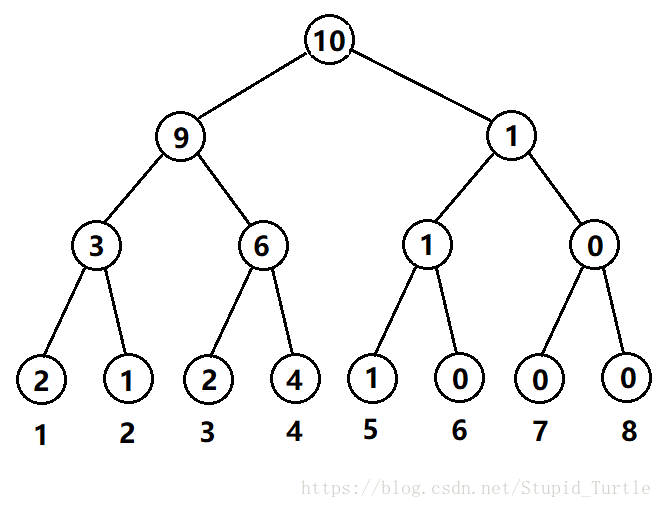
从网上搬的。节点中的数字代表节点对应区间中所有数的出现次数。
换句话说，
每个叶子节点的值： 代表 这个值的出现次数。
非叶子节点的值：代表了某一个值域内，所有值出现次数的和。
上面的权值线段树中，\(6,7,8\) 并没有出现，然而却被建出。如果序列的数 \(a_i\) 的取值范围是 \(w\)，那么我们的树就需要 \(O(w\log w)\) 的空间。这对于大部分题都是无法忍受的。
所以考虑动态开点。一般的线段树，对于节点 \(p\)，其 \(ls,rs\) 一般都是 \(p\times 2,p\times 2+1\)，而这里我们直接定义两个数组 ls[p],rs[p] 来表示节点 \(p\) 的左右儿子。
那么这样，我们会建出 \(O(n)\) 个叶子结点，而对于每一个叶子结点网上还有 \(O(\log w)\) 的深度，所以总的空间复杂度降为 \(O(n\log w)\)。
考虑如何用代码实现建树的过程。
inline void pushup(int p){
tr[p]=tr[ls[p]]+tr[rs[p]];
return;
}
inline void update(int &p,int l,int r,int now){
if(!p)p=++id;
if(l==r){
tr[p]++;
return;
}
int mid=(l+r)>>1;
if(now<=mid)update(ls[p],l,mid,now);
else update(rs[p],mid+1,r,now);
pushup(p);
return;
}
我们可以实现在 update 的过程用中 build。
我们将 \(p\) 传参，若 \(p\) 未出现过则直接用 ++id 来新建节点。
l,r 表示当前节点所代表的的区间。now 表示当前 update 往权值线段树中加入的值，那么我们就在对于包含 now 的全部区间上的值都加一。
剩下的部分在例题中具体实现。
二. 例题
相信大家都做过。
那么考虑使用权值线段树解法。
求逆序对，从左往右遍历数组，遍历到 \(i\) 时，检查一下已经遍历的值 \(a_1\sim a_{i-1}\) 中，有多少比它大的即可。
这可以用权值线段树来实现。
#include<bits/stdc++.h>
using namespace std;
const int N=1e7+8;
const int lim=1e9;
int tr[N],ls[N],rs[N],n,id,rt;
long long ans;
inline void pushup(int p){
tr[p]=tr[ls[p]]+tr[rs[p]];
return;
}
inline void update(int &p,int l,int r,int col){
if(!p)p=++id;
if(l==r){
tr[p]++;
return;
}
int mid=(l+r)>>1;
if(col<=mid)update(ls[p],l,mid,col);
else update(rs[p],mid+1,r,col);
pushup(p);
return;
}
inline long long query(int p,int l,int r,int now){//这里的now表示询问区间的左端点。右端点是 lim，所以不传参了。
if(!p)return 0;
if(l>now)return (long long)tr[p];//即有多少个大于x的数
int mid=(l+r)>>1;
long long res=0;
if(now<=mid)res+=query(ls[p],l,mid,now);
res+=query(rs[p],mid+1,r,now);//由于t是lim，所以必然大于mid，不需判断。
return res;
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
int x;
scanf("%d",&x);
update(rt,1,lim,x);//rt是当前权值线段树的根。
ans+=query(1,1,lim,x);//这里应该写query(1,1,lim,x,lim)，我将最后的lim省略了。
//这句两行相当于在权值线段树中加入 x，查询权值线段树中大于x的值的个数。
}
printf("%lld",ans);
return 0;
}
考虑在线段树节点里面额外维护一个信息 flag[p]，代表这个值域内，是否存在仅出现一次的元素。
然后询问时，优先询问右边（值域较大的部分）。
注意到值域 \(a_i\) 可能为负数，那么这是一个trick：给 \(a_i\) 加上 delta，使 \(a_i\) 为正。
那么对于此题 delta 就是 \(10^9\)。注意这样 lim 就变成 \(2\times 10^9\)。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=1e7+8;
const int lim=2e9;
const int delta=1e9;
int tr[N],ls[N],rs[N],flag[N],k,n,id,rt,a[N];
inline void pushup(int p){
tr[p]=tr[ls[p]]+tr[rs[p]];
flag[p]=flag[ls[p]]|flag[rs[p]];
return;
}
inline void update(int &p,int l,int r,int col,int val){
// cout<<p<<" "<<l<<" "<<r<<"*";
if(!p)p=++id;
if(l==r){
tr[p]+=val;
if(tr[p]==1)flag[p]=1;
else flag[p]=0;
return;
}
int mid=(r-l)>>1;
mid+=l;
if(col<=mid)update(ls[p],l,mid,col,val);
else update(rs[p],mid+1,r,col,val);
pushup(p);
return;
}
inline int query(int p,int l,int r){
if(!flag[p])return -1;
if(l==r)return l;
int mid=(r-l)>>1;
mid+=l;
// int mid=(ll)((l+r)>>1);
if(flag[rs[p]])return query(rs[p],mid+1,r);
else return query(ls[p],l,mid);
}
int main(){
scanf("%d%d",&n,&k);
for(int i=1;i<=n;i++)scanf("%d",&a[i]),a[i]+=delta;
for(int i=1;i<k;i++)update(rt,0,lim,a[i],1);
for(int i=1;i<=n-k+1;i++){
int j=i+k-1;
update(rt,0,lim,a[j],1);
int x=query(rt,0,lim);
if(x==-1)puts("Nothing");
else printf("%d\n",x-delta);
update(rt,0,lim,a[i],-1);
}
return 0;
}
权值线段树可以实现模板平衡树的全部功能。
虽然线段树常数比平衡树小，但是注意权值线段树的时间复杂度是 \(O(n\log w)\) 而不是 \(O(n\log n)\)。（\(w\) 指值域）
- 插入与删除
直接 update。
inline void pushup(int p){
tr[p]=tr[ls[p]]+tr[rs[p]];
return;
}
inline void update(int &p,int l,int r,int now,int val){
if(!p)p=++id;
if(l==r){
tr[p]+=val;
return;
}
int mid=(l+r)>>1;
if(now<=mid)update(ls[p],l,mid,now,val);
else update(rs[p],mid+1,r,now,val);
pushup(p);
return;
}
inline void add(int x){
update(rt,1,lim,x,1);
return;
}
inline void del(int x){
update(rt,1,lim,x,-1);
return;
}
- 查询 \(x\) 的排名
直接 query 在 \([1,x-1]\) 中的数的个数，那么答案即为其加一。
inline int query(int p,int l,int r,int s,int t){
if(s<=l&&r<=t)return tr[p];
int mid=(l+r)>>1,res=0;
if(s<=mid)res+=query(ls[p],l,mid,s,t);
if(mid<t)res+=query(rs[p],mid+1,r,s,t);
return res;
}
inline int rnk(int x){
if(x<=1)return 1;
return query(1,1,lim,1,x-1)+1;
}
- 查询第 \(k\) 大
当左子树内权值大于等于剩余查询个数，则递归进入左子树进行查询，否则递归进入右子树进行查询并减去左子树的权值。
inline int kth(int p,int l,int r,int now){
if(l==r)return l;
int mid=(l+r)>>1;
if(now<=tr[ls[p]])return kth(ls[p],l,mid,now);
else return kth(rs[p],mid+1,r,now-tr[ls[p]]);
}
- 前驱后继
以前驱为例。
考虑对于 \([l,r]\) 与 \(x\) 的关系分类。
若 \(r<x\)，则直接查询 \([l,r]\) 区间中最右的点。
若 \(x>mid+1\) 且 \(p\) 有右儿子，优先查询 \([mid+1,r]\) 中是否有 \(<x\) 的节点。
若以上都不符合则查询 \([l,mid]\)。
后继同理。
inline int findpre(int p,int l,int r){//查询[l,r]区间内最右的点
if(l==r)return l;
int mid=(l+r)>>1;
if(tr[rs[p]])return findpre(rs[p],mid+1,r);
else return findpre(ls[p],l,mid);
}
inline int pre(int p,int l,int r,int now){
int mid=(l+r)>>1;
if(r<now){
if(tr[p])return findpre(p,l,r);
else return 0;
}
else if(now>mid+1&&tr[rs[p]]){
int res=pre(rs[p],mid+1,r,now);
if(res)return res;
}
return pre(ls[p],l,mid,now);
}
inline int findnxt(int p,int l,int r){
if(l==r)return l;
int mid=(l+r)>>1;
if(tr[ls[p]])return findnxt(ls[p],l,mid);
else return findnxt(rs[p],mid+1,r);
}
inline int nxt(int p,int l,int r,int now){
int mid=(l+r)>>1;
if(l>now){
if(tr[p])return findnxt(p,l,r);
else return 0;
}
else if(now<=mid&&tr[ls[p]]){
int res=nxt(ls[p],l,mid,now);
if(res)return res;
}
return nxt(rs[p],mid+1,r,now);
}
总代码：
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+6;
const int lim=2e7;
const int M=1e7+8;
const int delta=1e7;
int tr[M],ls[M],rs[M],id,rt,n;
inline void pushup(int p){
tr[p]=tr[ls[p]]+tr[rs[p]];
return;
}
inline void update(int &p,int l,int r,int now,int val){
if(!p)p=++id;
if(l==r){
tr[p]+=val;
return;
}
int mid=(l+r)>>1;
if(now<=mid)update(ls[p],l,mid,now,val);
else update(rs[p],mid+1,r,now,val);
pushup(p);
return;
}
inline void add(int x){
update(rt,1,lim,x,1);
return;
}
inline void del(int x){
update(rt,1,lim,x,-1);
return;
}
inline int query(int p,int l,int r,int s,int t){
if(s<=l&&r<=t)return tr[p];
int mid=(l+r)>>1,res=0;
if(s<=mid)res+=query(ls[p],l,mid,s,t);
if(mid<t)res+=query(rs[p],mid+1,r,s,t);
return res;
}
inline int rnk(int x){
if(x<=1)return 1;
return query(1,1,lim,1,x-1)+1;
}
inline int kth(int p,int l,int r,int now){
if(l==r)return l;
int mid=(l+r)>>1;
if(now<=tr[ls[p]])return kth(ls[p],l,mid,now);
else return kth(rs[p],mid+1,r,now-tr[ls[p]]);
}
inline int findpre(int p,int l,int r){
if(l==r)return l;
int mid=(l+r)>>1;
if(tr[rs[p]])return findpre(rs[p],mid+1,r);
else return findpre(ls[p],l,mid);
}
inline int pre(int p,int l,int r,int now){
int mid=(l+r)>>1;
if(r<now){
if(tr[p])return findpre(p,l,r);
else return 0;
}
else if(now>mid+1&&tr[rs[p]]){
int res=pre(rs[p],mid+1,r,now);
if(res)return res;
}
return pre(ls[p],l,mid,now);
}
inline int findnxt(int p,int l,int r){
if(l==r)return l;
int mid=(l+r)>>1;
if(tr[ls[p]])return findnxt(ls[p],l,mid);
else return findnxt(rs[p],mid+1,r);
}
inline int nxt(int p,int l,int r,int now){
int mid=(l+r)>>1;
if(l>now){
if(tr[p])return findnxt(p,l,r);
else return 0;
}
else if(now<=mid&&tr[ls[p]]){
int res=nxt(ls[p],l,mid,now);
if(res)return res;
}
return nxt(rs[p],mid+1,r,now);
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
int op,x;
scanf("%d%d",&op,&x);
x+=delta;
if(op==1)add(x);
else if(op==2)del(x);
else if(op==3)printf("%d\n",rnk(x));
else if(op==4)printf("%d\n",kth(rt,1,lim,x-delta)-delta);
else if(op==5)printf("%d\n",pre(rt,1,lim,x)-delta);
else printf("%d\n",nxt(rt,1,lim,x)-delta);
}
return 0;
}
习题：
三元上升子序列的个数=每个数前比它小的数的个数 乘上 每个数后比它大的数的个数之和。
那么只需要维护每个数前比它小的数的个数 和 每个数后比它大的数的个数。这类似于逆序对的做法，实现容易。
考虑冒泡排序的本质与对逆序对个数的变化，发现规律后就显然了，使用树状数组或权值线段树维护逆序对都可以。
先考虑给序列弄前缀和。然后对于 \(\sum\limits_{i=l}^ra_i<t\) 转为 \(a_r-a_{l-1}<t\)。考虑插入 \(a_i\) 后查询 \(1\sim a_{i-1}+t-1\) 中数的个数。
遍历到 \(i\) 时，令 \(f_j\) 为目前结尾的值为 \(j\) 的 subsequence 的最大长度。
那么 \(f_{h_i} = \max\limits_j \{ f_j+1 \}\)，其中 \(|h_i - j| \geq d\)
这个 \(f\) 就可以用权值线段树来维护。
查询的时候，分别查询 \(j \geq h_i + d\) 和 \(j \leq h_i - d\) 的部分即可。
