力扣-1353. 最多可以参加的会议数目
1.题目介绍
题目地址(1353. 最多可以参加的会议数目 - 力扣(LeetCode))
https://leetcode.cn/problems/maximum-number-of-events-that-can-be-attended/
题目描述
给你一个数组 events,其中 events[i] = [startDayi, endDayi] ,表示会议 i 开始于 startDayi ,结束于 endDayi 。
你可以在满足 startDayi <= d <= endDayi 中的任意一天 d 参加会议 i 。在任意一天 d 中只能参加一场会议。
请你返回你可以参加的 最大 会议数目。
示例 1:
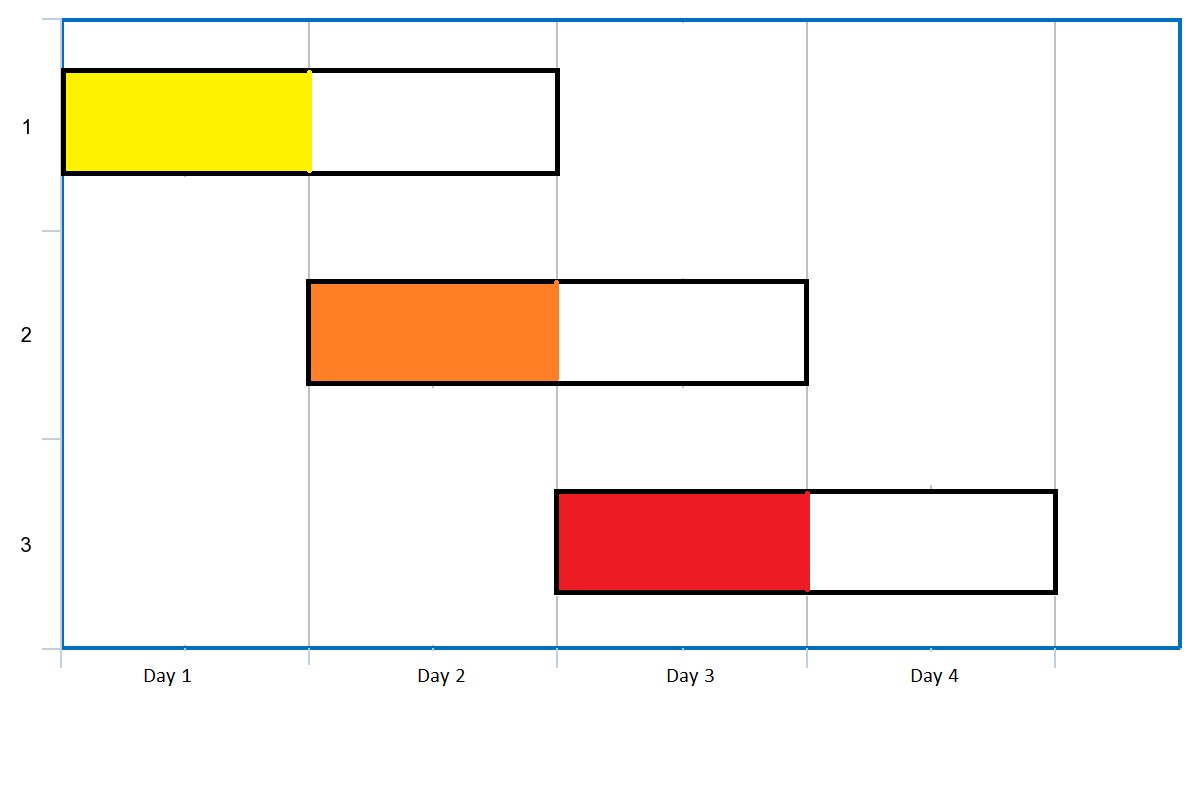
输入:events = [[1,2],[2,3],[3,4]] 输出:3 解释:你可以参加所有的三个会议。 安排会议的一种方案如上图。 第 1 天参加第一个会议。 第 2 天参加第二个会议。 第 3 天参加第三个会议。
示例 2:
输入:events= [[1,2],[2,3],[3,4],[1,2]] 输出:4
提示:
1 <= events.length <= 105events[i].length == 21 <= startDayi <= endDayi <= 105
2.题解
2.1 贪心算法 + 优先级队列(小根堆)
思路
这里我们思考最优贪心策略:
从左到右遍历时间点i,某会议x在满足起始时间startTime大于i(必要条件,否则无法参加),同时结束时间endTime是最早的(因为它结束时间最早,所以相比那些结束时间晚的更容易被淘汰,故优先选择),每次都选择这样的会议参加或者该时间点没有会议参加,局部最优达成全局最优。
那我们就要考虑进行实现了,首先要维护当前时间点i,可以参加的所有会议(并不是所有会议都开始了)
我们并不想维护一个长度为max_TimeEnd的vector数组,并记录其中所有可以参与的会议(这样我们要遍历max_TimeEnd次数组,而且还要花费非常多的额外空间进行维护)
我们选择使用优先级队列进行动态维护,当当前会议开始后,就将该会议加入到队列中;当当前会议到达结束时间后/我们选择参与了该会议,我们将该会议从队列去除。
还有一个问题,我们该如何根据当前时间i,快速判断有哪些会议开始,又有哪些会议结束呢?
如果使用原来的数组,我们每次选择都要从头到尾遍历一遍并进行判断,这十分的耗费时间,
所以我们选择使用一个哈希表来维护:开始时间--结束时间的映射(这里一个开始时间可能对应多个结束时间,比如像多个会议都是时间i开始,但结束时间不一样,所以第二个参数是vector)
当我们得知当前时间后,就可以用mp.count(i)判断是否有当前日期i开始的会议,并根据映射将mp[i]中存储的结束时间加到优先级队列中,这样就维护了进队操作。
这里我们使用一个基于小根堆的优先级队列,队列存储的是各个会议的结束时间,这样就可以在选择会议时让结束时间早的会议优先出队!
同时对于结束时间 < 当前时间的会议, 说明其已经结束了,不可能再进行选择, 我们也要将其出队。 这样就维护了出队操作
代码
- 语言支持:C++
C++ Code:
class Solution {
public:
int maxEvents(vector<vector<int>>& events) {
unordered_map<int, vector<int>> mp;
int cnt = 0;
int max_day = 0; // 用于记录所有活动中最晚的结束时间,确定遍历结束点
for(vector<int> event : events){
// 记录开始时间和结束时间的映射,便于下文我们进行寻找
mp[event[0]].push_back(event[1]);
max_day = max(max_day, event[1]);
}
// 自底向上,将最早(小)结束的排在前面,所以greater(父节点 > 子节点的值就交换,将大的值沉底)
priority_queue<int, vector<int>, greater<int>> q;
// 从左到右遍历每一天,看每一天是否有会议可以参加
for(int i = 0; i <= max_day; i++){
// 如果有今天开始的会议,加入优先级队列
if(mp.count(i)){
for(int endTime : mp[i]){
q.push(endTime);
}
}
// 去除在今天i已经结束的队列成员
while(!q.empty() && q.top() < i){
q.pop();
}
// 选择一个结束最早的会议参加
if(!q.empty()){
cnt++;
q.pop();
}
}
return cnt;
}
};
复杂度分析
令 n 为数组长度。
- 时间复杂度:\(O(n)\)
- 空间复杂度:\(O(n)\)


