力扣-189. 轮转数组
1.题目
题目地址(189. 轮转数组 - 力扣（LeetCode）)
https://leetcode.cn/problems/rotate-array/
题目描述
给定一个整数数组 nums，将数组中的元素向右轮转 k 个位置，其中 k 是非负数。
示例 1:
输入: nums = [1,2,3,4,5,6,7], k = 3 输出:[5,6,7,1,2,3,4]解释: 向右轮转 1 步:[7,1,2,3,4,5,6]向右轮转 2 步:[6,7,1,2,3,4,5]向右轮转 3 步:[5,6,7,1,2,3,4]
示例 2:
输入：nums = [-1,-100,3,99], k = 2 输出：[3,99,-1,-100] 解释: 向右轮转 1 步: [99,-1,-100,3] 向右轮转 2 步: [3,99,-1,-100]
提示：
1 <= nums.length <= 105-231 <= nums[i] <= 231 - 10 <= k <= 105
进阶：
- 尽可能想出更多的解决方案，至少有 三种 不同的方法可以解决这个问题。
- 你可以使用空间复杂度为
O(1)的 原地 算法解决这个问题吗？
2.题解
2.1 新数组存储(空间换时间)
思路
使用一个新数组存储移动k次后的数组状况, 注意索引对应关系即可
最后使用assign函数更新原数组nums即可
代码
class Solution{
public:
void rotate(vector<int>& nums, int k) {
int n = nums.size();
k %= n;
vector<int> arr(n);
for(int i = 0; i < n; i++){
arr[(i + k) % n] = nums[i];
}
nums.assign(arr.begin(), arr.end());
}
};
2.2 环状替换
思路
我们之所以不直接将nums[(i+k)%n]替换为nums[i], 是因为这么操作就会使我们丢失关于nums[(i+k)%n]的数据,导致错误;
那么如果我们每次在替换之前用一个临时变量temp存储nums[(i+k)%n]的数据呢? 那我们就可以从第一个数据开始, 向后替换直到再次回到第一个数据
但是这时不一定遍历完了整个数组, 我们必须知道结束条件----目前已经遍历了多少个数,如果已完成(等于数组个数)就结束;反之向后推进一个数,再次展开循环.
由于最终回到了起点，故该过程恰好走了整数数量的圈,所以假设我们总共遍历了a次数组, 数组长度为n, 遍历了b个元素, 每个元素之间的差值为 k.
我们有 an=bk，即 an一定为 n,k 的公倍数(b暂时未知,所以不纳入讨论)
又因为我们要求第一次回到起点时便结束这次遍历,所以a尽可能的小(a可能是最小圈数的任意倍数,但是我们只需要最小倍数即可,无需重复跑圈)
故 an 就是 n,k 的最小公倍数 lcm(n,k), b 就为 lcm(n,k)/k
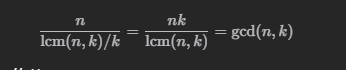
这说明单次遍历会访问到 lcm(n,k)/k 个元素。为了访问到所有的元素，我们需要进行遍历的次数为
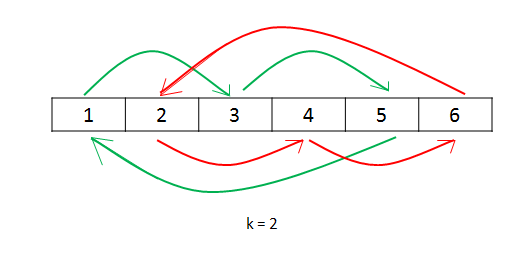
如上, a刚好为n,k的最大公约数,所以我们设置一个外循环规定遍历圈数(也就是第一次起始点和第一次结束时起始点和后面一个被遍历过元素之间所有未被遍历的点(作为循环起始点再次开始循环))
代码
class Solution{
public:
void rotate(vector<int>& nums, int k) {
int n = nums.size();
k %= n;
int count = gcd(n, k); // 一次循环有等式 (an = bk = lcd(n,k) [要求a最小]), 该次循环遍历 b = lcd(n,k) / k 个元素, 那么遍历完n个元素, 需要循环 n / b = nk / (lcd(n,k)) = gcd(n,k)次
for(int start = 0; start < count; start++){
int current = start , preVal = nums[start]; // 记录当前元素位置 和 前一个元素的值(避免被后面的元素值覆盖)
do{
int next = (current + k) % n; // 记录下一个元素位置
// 可以简化为 swap(preVal, nums[next]);
int temp = nums[next];
nums[next] = preVal;
preVal = temp;
current = next;
}while(current != start); // 这里不能使用next,因为其是循环内部元素
}
}
};
2.3 翻转数组(镜像)
思路
这里进行了一个优化k %= nums.size(); // 由于每数组长度次数的移动后,恢复为原数组,所以先减少移动次数到一个数组大小内
原理: 任何一个数组翻转两次后和原数组相同
对于[1,2,3,4,5,6,7], k = 3
1.我们首先进行翻转(镜像) [7,6,5,4,3,2,1]
2.我们将从后端移动至首部的部分看做一个镜像数组(步骤1进行了镜像),所以再次翻转得到实际数组
3.同理,后面部分也看做一个镜像数组,再次翻转得到实际数组
代码
- 语言支持：C++
C++ Code:
class Solution{
public:
void rotate(vector<int>& nums, int k) {
k %= nums.size();
reverse(nums,0,nums.size()-1);
reverse(nums,0,k-1);
reverse(nums,k, nums.size()-1);
}
void reverse(vector<int>& nums,int start, int end){
while (start < end){
swap(nums[start++],nums[end--]);
}
}
};
复杂度分析
令 n 为数组长度。
- 时间复杂度：\(O(n)\)
- 空间复杂度：\(O(1)\)
