912. 排序数组---快速排序
1.题目介绍
给你一个整数数组 \(nums\)，请你将该数组升序排列。
示例 1：
输入：nums = [5,2,3,1]
输出：[1,2,3,5]
示例 2：
输入：nums = [5,1,1,2,0,0]
输出：[0,0,1,1,2,5]
提示：
- \(1 <= nums.length <= 5 * 10^{4}\)
- \(-5 * 10^{4} <= nums[i] <= 5 * 10^{4}\)
2.题解
2.1随机化快速排序（快慢指针）
思路
如何和把选定的基点数据挪到正确位置上，这是快速排序的核心，我们称为 Partition。
过程如下所示，其中 i 为当前遍历比较的元素位置：
代码
public class Solution {
public int[] sortArray(int[] nums) {
quicksort(nums, 0, nums.length - 1);
return nums;
}
private void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
private int partition(int[] nums, int start, int end) {
int randomIndex = new Random().nextInt(end - start + 1) + start;
swap(nums, randomIndex, start);
int pivot = nums[start];
int j = start;
for (int i = start + 1; i <= end; i++) {
if (nums[i] < pivot) {
j++;
swap(nums, j, i);
}
}
swap(nums, start, j);
return j;
}
private void quicksort(int[] nums, int start, int end) {
if (start >= end) {
return;
}
int pivotIndex = partition(nums, start, end);
quicksort(nums, start, pivotIndex - 1);
quicksort(nums, pivotIndex + 1, end);
}
}
#include<bits/stdc++.h>
using namespace std;
void swap(vector<int> &arr, int i, int j){
int temp;
temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
int partition(vector<int> &arr, int begin, int end){
srand((unsigned)time(NULL));
int randNum = rand() % (end - begin + 1) + begin;
int j = begin, currNum = arr[randNum];
swap(arr, begin, randNum);
for(int i = begin + 1; i <= end; i++){
if(arr[i] < currNum){
j++;
swap(arr, i, j);
}
}
swap(arr, begin, j);
return j;
}
void quicksort(vector<int> &arr, int begin, int end){
if(begin >= end) return;
int medium = partition(arr, begin, end);
quicksort(arr, begin, medium - 1);
quicksort(arr, medium + 1, end);
}
void sortArray(vector<int> &arr){
int length = arr.size();
quicksort(arr, 0, length - 1);
}
int main(){
int n, j;
cin >> n;
vector<int> a(n);
for (int i = 0; i < n; i++){
cin >> a[i];
}
sortArray(a);
for (int i = 0; i < n; i++){
cout << a[i] << ' ';
}
}
优点（相对于普通快速排序）
如果是对近乎有序的数组进行快速排序，每次 partition 分区后子数组大小极不平衡，容易退化成 O(n^2) 的时间复杂度算法。我们需要对上述代码进行优化，随机选择一个基点做为比较，称为随机化快速排序算法。只需要在上述代码前加上下面一行，随机选择数组中一数据和基点数据进行交换。
示例数据：
缺点
对于有大量重复元素的数组，如果使用上一节随机化快速排序效率是非常低的，导致 partition 后大于基点或者小于基点数据的子数组长度会极度不平衡，甚至会退化成 O(n*2) 时间复杂度的算法
具体问题情况请参考：快速排序优化-双路快速排序法
这里可以想到，不管是把小于等于"v"的元素放到橙色部分，还是把大于等于"v"的元素放到橙色部分，当我们整个数组中包含有大量重复键值的时候，Partition过程都非常有可能把整个数组分成极度不平衡的两个部分，这是因为对于每个键值来说重复的元素太多了，我们选的键值稍微有一点不平衡的话，两部分的差距就会特别的大。
2.2双路快速排序（首尾指针）
思路
时间和空间复杂度同随机化快速排序。
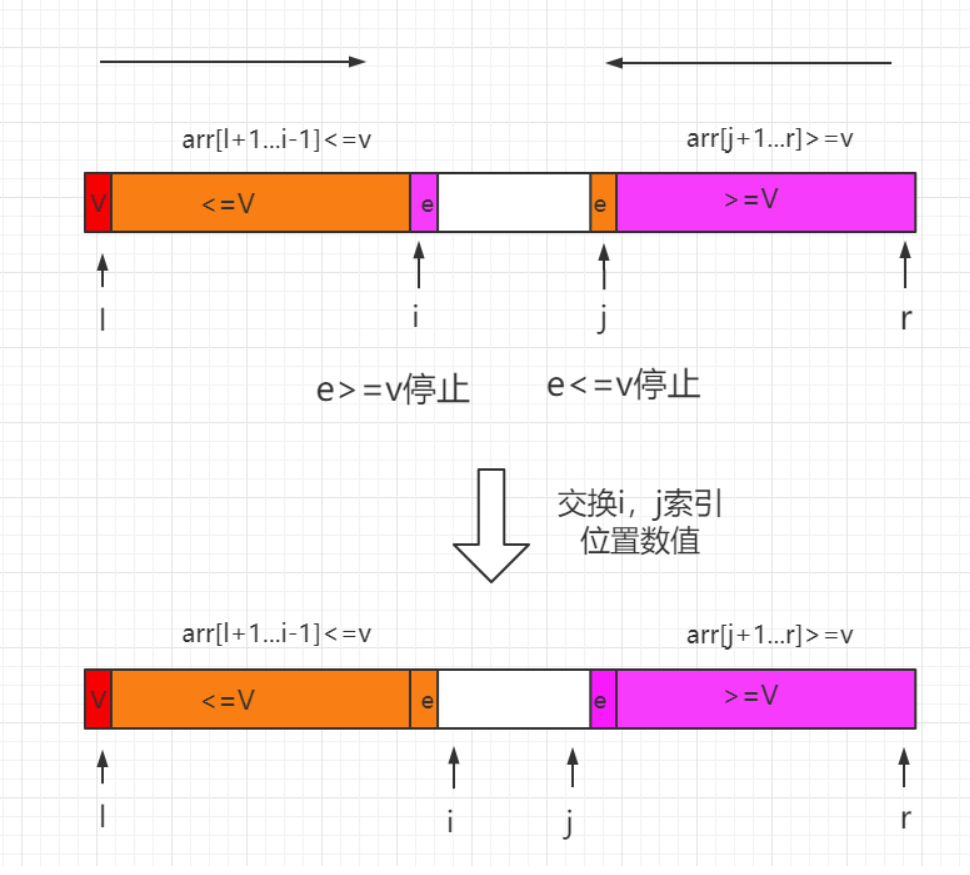
使用两个索引值（i、j）用来遍历我们的序列，将 <=v 的元素放在索引 i 所指向位置的左边，而将 >=v 的元素放在索引 j 所指向位置的右边，平衡左右两边子数组。
而不是一股脑将=v的数据放在某一边，而是均衡到两边的序列，这样就不会出现长度极端失衡的情况了！
代码
class Solution {
public int[] sortArray(int[] nums) {
quicksort(nums,0,nums.length-1);
return nums;
}
public void swap(int[] nums, int i, int j){
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
public void quicksort(int[] nums, int start, int end){
if (start > end) return;
int v = new Random().nextInt(end-start+1)+start;
swap(nums,v,start);
int ans = nums[start];
int i = start, j = end;
// 进行一轮循环
while (start != end){
// end开始逆向寻找比基准数小的
while (true){
if (start >= end || nums[end] < ans) break;
end--;
}
// start开始正向寻找比基准数大的
while (true){
if (start >= end || nums[start] > ans) break;
start++;
}
// 交换两数
swap(nums,start,end);
}
// 结束一轮循环，将基准数与start/end当前所在位置交换
swap(nums,i, start);
quicksort(nums,i,start-1);
quicksort(nums,start+1,j);
}
}
#include<bits/stdc++.h>
using namespace std;
void swap(vector<int> &arr, int i, int j){
int temp;
temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
int partition(vector<int> &arr, int begin, int end){
srand((unsigned)time(NULL));
int randNum = rand() % (end - begin + 1) + begin;
int start = begin, currNum = arr[randNum];
swap(arr, begin, randNum);
while(begin < end){
while(begin < end && arr[end] >= currNum){
end--;
}
while(begin < end && arr[begin] <= currNum){
begin++;
}
if (begin < end) {
swap(arr, begin, end);
}
}
swap(arr, start, begin);
return begin;
}
void quicksort(vector<int> &arr, int begin, int end){
if(begin >= end) return;
int medium = partition(arr, begin, end);
quicksort(arr, begin, medium - 1);
quicksort(arr, medium + 1, end);
}
void sortArray(vector<int> &arr){
int length = arr.size();
quicksort(arr, 0, length - 1);
}
int main(){
int n, j;
cin >> n;
vector<int> a(n);
for (int i = 0; i < n; i++){
cin >> a[i];
}
sortArray(a);
for (int i = 0; i < n; i++){
cout << a[i] << ' ';
}
}
2.3三路快速排序
思路
三路快速排序是双路快速排序的进一步改进版本，三路排序算法把排序的数据分为三部分，分别为小于 v，等于 v，大于 v，
v 为标定值，这样三部分的数据中，等于 v 的数据在下次递归中不再需要排序，小于 v 和大于 v 的数据也不会出现某一个特别多的情况），通过此方式三路快速排序算法的性能更优。
最终[low,lt)为小于基准数，[lt,gt]为等于基准数, (gt,high]为大于基准数
我们分三种情况进行讨论 partiton 过程，i 表示遍历的当前索引位置：
（1）当前处理的元素 e=V，元素 e 直接纳入蓝色区间，同时i向后移一位。
（2）当前处理元素 e<v，e 和等于 V 区间的第一个位置数值进行交换，同时索引 lt 和 i 都向后移动一位
（3）当前处理元素 e>v，e 和 gt-1 索引位置的数值进行交换，同时 gt 索引向前移动一位。
最后当 i=gt 时，结束遍历，同时需要把 v 和索引 lt 指向的数值进行交换，这样这个排序过程就完成了，然后对 <V 和 >V 的数组部分用同样的方法再进行递归排序。
代码
class Solution {
public int[] sortArray(int[] nums) {
quicksort(nums, 0, nums.length - 1);
return nums;
}
public void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
public void quicksort(int[] nums, int low, int high) {
if (low >= high) {
return;
}
int pivot = nums[low];
int lt = low; // less than pivot
int gt = high; // greater than pivot
int i = low + 1;
while (i <= gt) {
if (nums[i] < pivot) {
swap(nums, i, lt);
lt++;
i++;
} else if (nums[i] > pivot) {
swap(nums, i, gt);
gt--;
} else {
i++;
}
}
quicksort(nums, low, lt - 1);
quicksort(nums, gt + 1, high);
}
}
#include<bits/stdc++.h>
using namespace std;
void swap(vector<int> &arr, int i, int j){
int temp;
temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
pair<int, int> partition(vector<int>& arr, int begin, int end) {
srand((unsigned)time(NULL));
int randNum = rand() % (end - begin + 1) + begin;
int currNum = arr[randNum];;
int i = begin, lt = begin, gt = end;
swap(arr, begin, randNum);
while (i <= gt) { //gt前一个才是已排好的序列，gt还是留白，只有当i跨过gt才是匹配完成了
if (arr[i] < currNum) {
swap(arr, lt, i);//这个lt已经是小于currNum的了
lt++;//这里lt++表明当前lt是已排好 的小于currNum集合的下一个元素
i++;//i总是指向下一个需要排序的数
}
else if (arr[i] == currNum){
i++;
}
else{
swap(arr, i, gt);//这个gt已经是大于currNum的了
gt--;//这里gt--表明gt总是指向已排好 的大于currNum集合的前一个元素
}
}
return make_pair(lt, gt);
}
void quicksort(vector<int>& arr, int begin, int end) {
if (begin >= end)
return;
pair<int, int> pos = partition(arr, begin, end);
int lt = pos.first, gt = pos.second;
quicksort(arr, begin, lt - 1);//lt指向已排好小于currNum的下一个，所以这里是lt-1
quicksort(arr, gt + 1, end);//gt指向已排好大于currNum的前一个，所以这里是gt+1
}
void sortArray(vector<int> &arr){
int length = arr.size();
quicksort(arr, 0, length - 1);
}
int main(){
int n, j;
cin >> n;
vector<int> a(n);
for (int i = 0; i < n; i++){
cin >> a[i];
}
sortArray(a);
for (int i = 0; i < n; i++){
cout << a[i] << ' ';
}
}
