拓扑排序

一、定义

拓扑排序(Topological Order)是指，将一个有向无环图(Directed Acyclic Graph简称DAG)进行排序进而得到一个有序的线性序列。

这样说，可能理解起来比较抽象。下面通过简单的例子进行说明！
例如，一个项目包括A、B、C、D四个子部分来完成，并且A依赖于B和D，C依赖于D。现在要制定一个计划，写出A、B、C、D的执行顺序。这时，就可以利用到拓扑排序，它就是用来确定事物发生的顺序的。

在拓扑排序中，如果存在一条从顶点A到顶点B的路径，那么在排序结果中B出现在A的后面。

二、算法思想

记录每个节点的入度和出度，入度为0 的节点为拓扑序列头部。

从上一节点得到下一节，从中选择入度最小的节点加入拓扑序列。

当得到加入拓扑序列的节点出度为0时，排序结束。

如果序列中的节点数少于总节点数，说明该图不是DAG，无法进行拓扑排序。

例：

这是一个简单的DAG

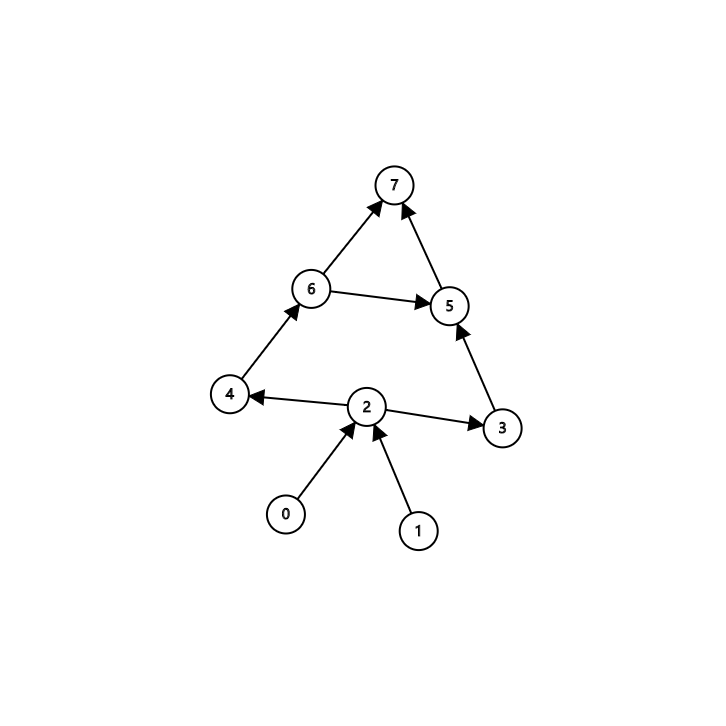
拓扑排序步骤如下：
（1）定义一个队列Q，并把所有入度为0的结点加入队列
（2）取队首结点，访问输出，然后删除所有从它出发的边，并令这些边到达的顶点的入度减1，如果某个顶点的入度减为0，则将其加入队列。
（3）重复进行（2）操作，直到队列为空。如果队列为空时入过队的结点数恰好为N，说明拓扑排序成功，图G为有向无环图；否则，拓扑排序失败，图G有环。

结点0和1的入度都为0，可以任意访问，但是结点2必须在结点0和1访问完之后才能访问，同理结点3和4必须在结点2访问完以后才能访问，但是结点3和4 之间没有依赖关系，结点5必须在结点3和结点6访问之后才能访问，等等.....
因此，对于上图的一个拓扑序列可以是：0,1,2,3,4,6,5,7 也可以是：0,1,2,4,6,3,5,7

拓扑排序两种做法：

​ 1、采用朴素做法，使用二维数组存储有向图

​ 2、使用邻接表存储有向图

ACwing848有向图的拓扑序列>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>AC代码

HDU1285确定比赛名次>>>>>>>>>>>>>AC代码1>>>>>>>>>>>>>>AC代码2