[学习记录]intel-ML课程记录04
本次课主要讲正则化、特征选取以及梯度下降(部分内容参考了链接1,链接2)
在先前的讨论中,我们发现K值越高,或是线性回归的阶数越高,一定程度能够对训练数据产生更好的拟合效果,但是对于测试数据而言误差也许非常大,即过拟合

正则化就能够用来解决因为特征过多导致的过拟合问题

βj即惩罚项,用来减少某一个特征所带来的影响,λ作为系数作为控制参数,可以使各个参数都不会太大,从而防止过拟合。但λ过大也会导致欠拟合
在上述成本函数中,除了通过惩罚减小参数,同时由于平方的影响,参数越大,收到的惩罚越严重。这叫做岭回归(L2)。
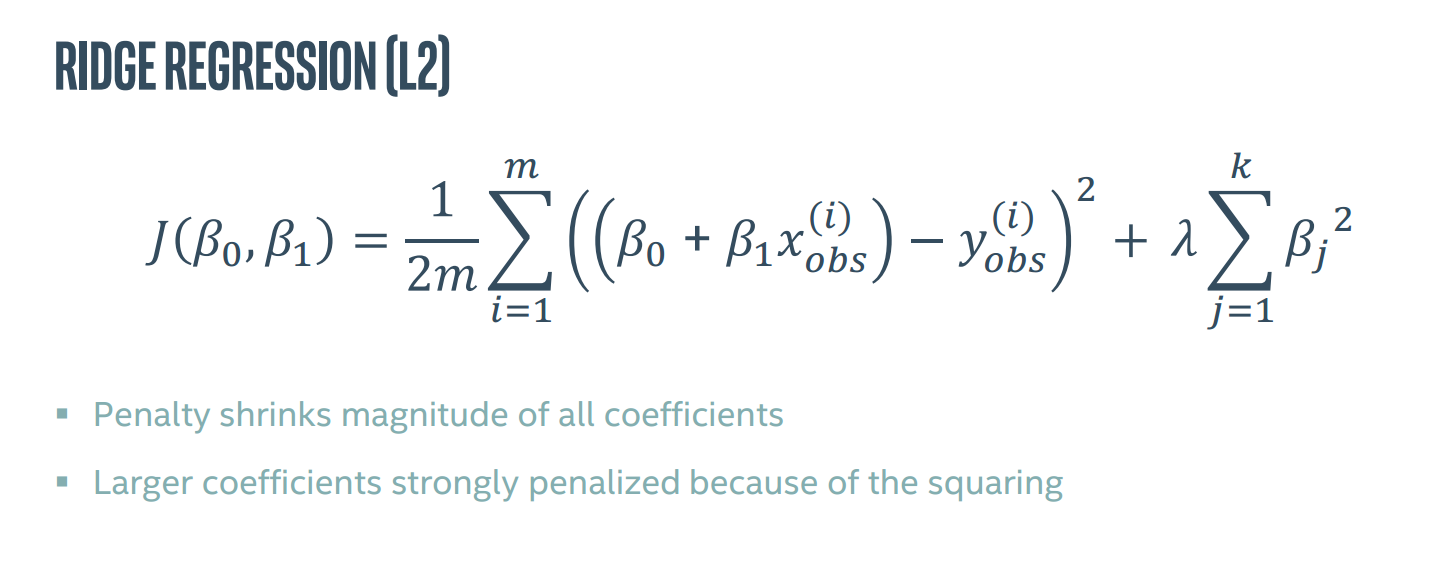

还有一种叫做lasso回归,即取绝对值,可用于特征选择,惩罚会选择性地缩小一些系数,但收敛比岭回归慢。
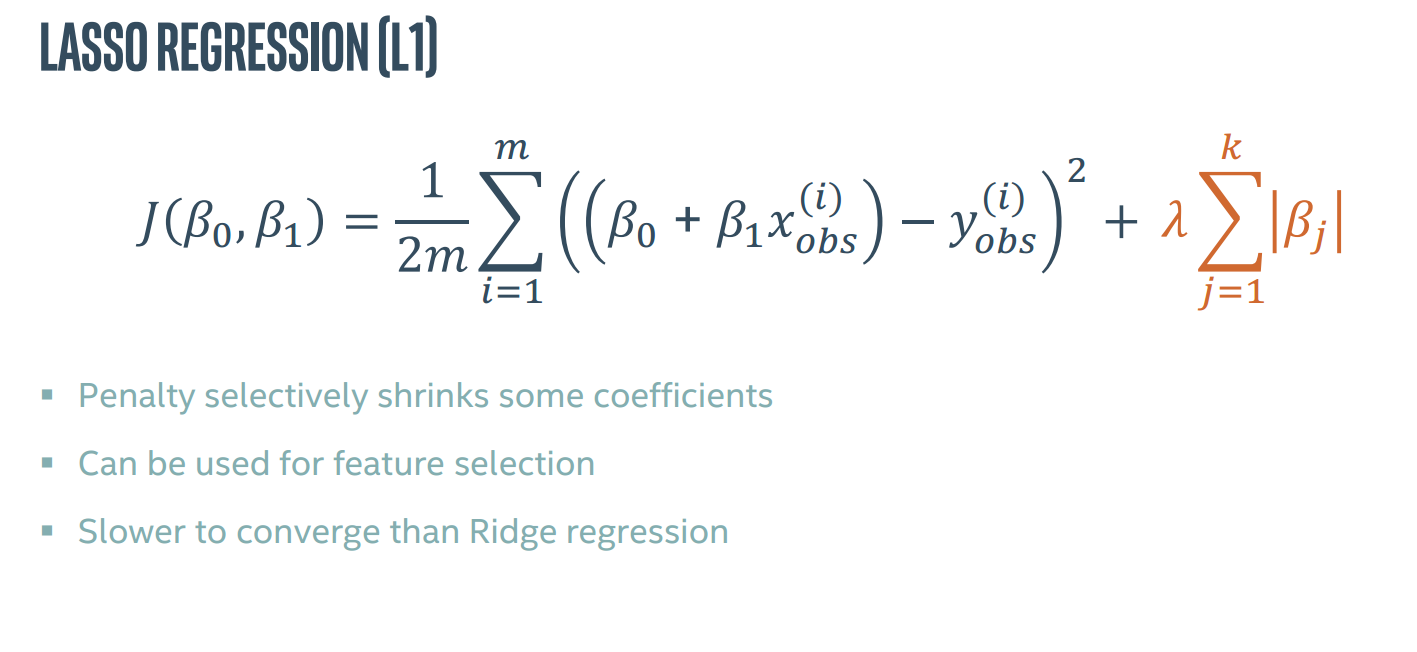

弹性网络回归,是一种对L1和L2的妥协,调整不同的参数控制两种回归的惩罚度


上面三种正则化方法都涉及到参数λ的选择,目前λ往往是依靠经验确定的,在调整λ时不能使用训练集,而是再分出一个验证集用来调整。

以下给出实例
岭回归,参数alpha就是λ。ridgecv类会对验证集进行交叉验证。

lasso回归,基本同岭回归

弹性网络回归,alpha为λ_L1,l1_ratio=λ_L1/λ_L2

特征选择
正则化方法通过减少特征的贡献从而实现特征选择。对于L1正则化来说,将部分特征贡献减至0即完成了特征选择。当然特征选择也能通过移除某一个特征来实现。
进行特征选择的意义在于
(1)减少特征数量是为了防止过度拟合
(2)对于部分模型,较少的特征可以有效缩短拟合时间,提高拟合效果
(3)同时确定最关键的特征也有利于提高模型的可解释性
下面给出实例
est为使用的模型的样例,n_features_to_select为最后剩下的参数的个数

梯度下降
梯度下降想找到一个全局代价最低点,通过求导数
对于之前我们讨论的成本函数J(β0,β1),也许图像是这样的,梯度是一个矢量,由各个参数在该点的导数组成。

我们从一个点出发,通过该点的梯度寻找下一个点,逐级找下去最终希望找到全局最低点,通过一个α来控制每次前进的步幅。
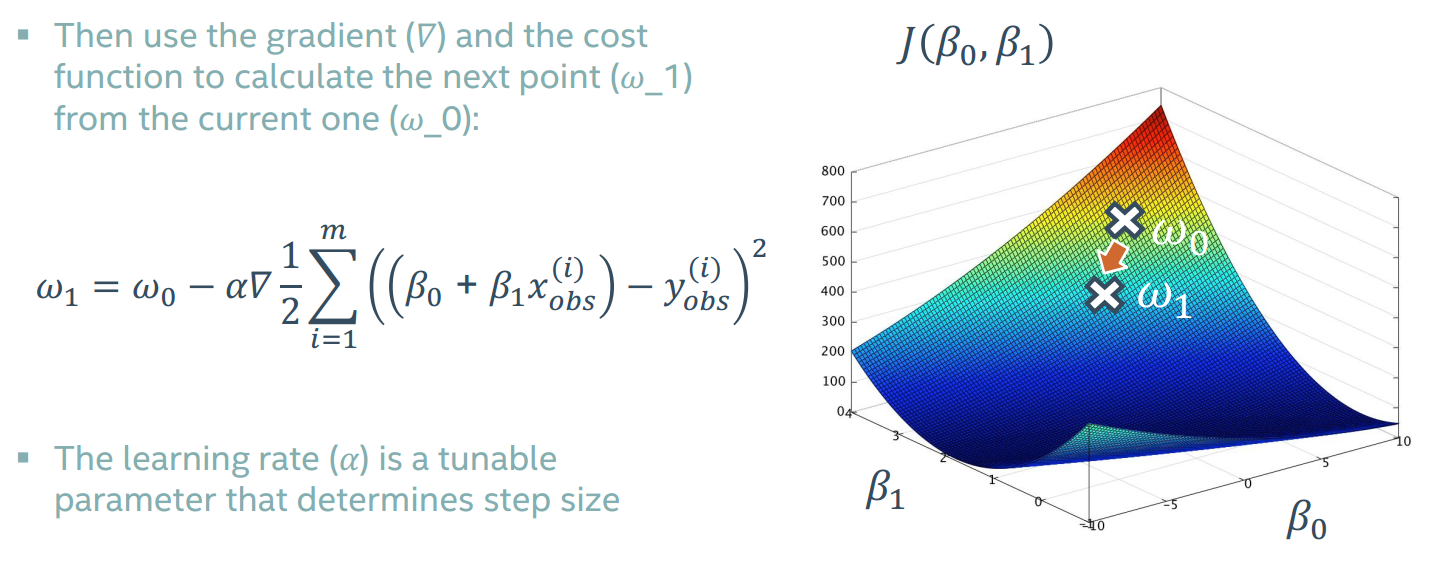
用这种方法叫做线性回归梯度下降方法

还有一种叫做随机梯度下降算法,使用单一点而不是所有点进行计算。
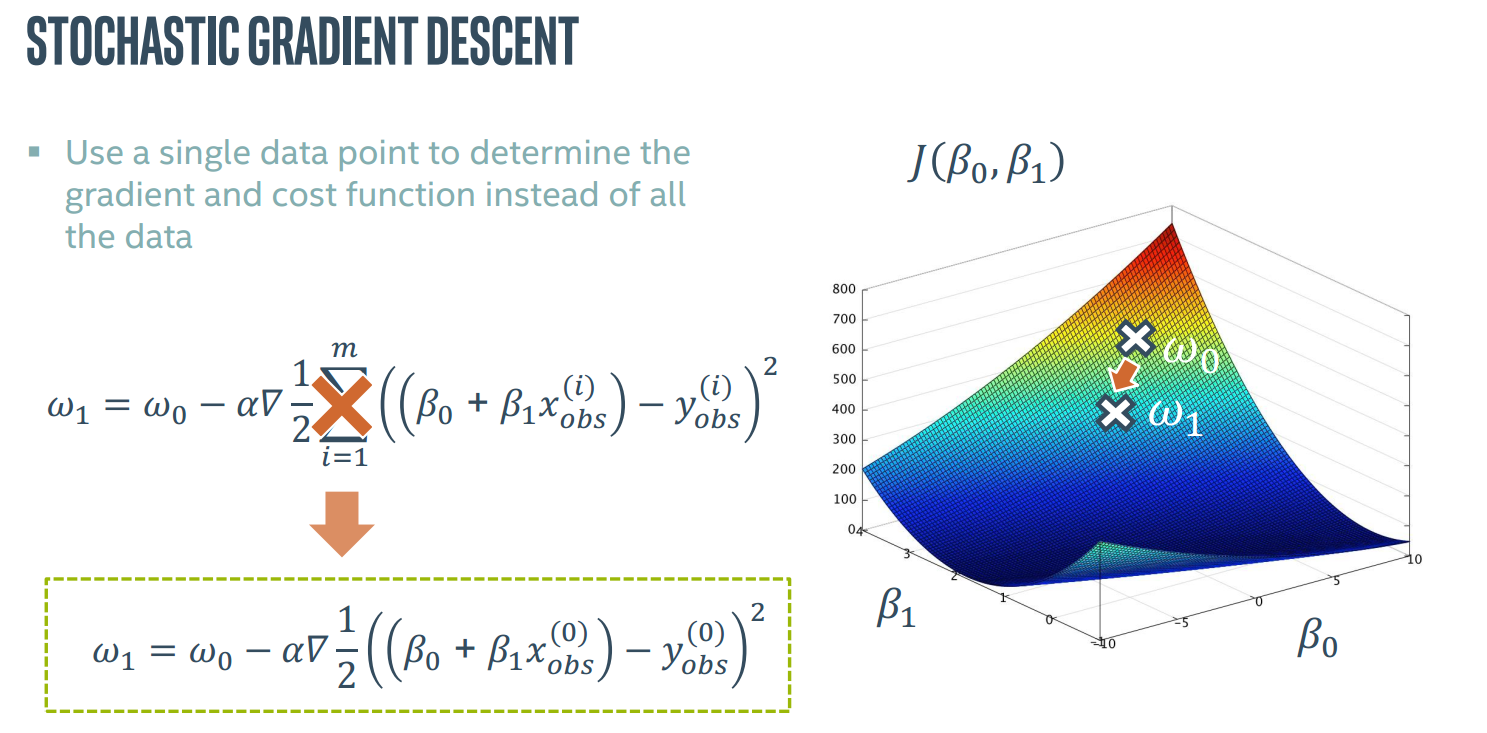
由于路径是直接由单一点产生的容易受噪音影响,所以有点“随机”

最小批梯度下降算法
注意是n而不是m,每训练n个作为一批进行梯度下降,是目前最好的梯度下降算法,也不像随机梯度下降那样容易受噪音影响。

(1)通常用于神经网络的迷你批处理实现
(2)批的大小在50-256之间
(3)批的大小与学习速率都需要权衡
(4)学习率应该随着时间增加而降低
实例
随机梯度下降:loss='squared_loss'声明是线性回归,alpha为学习速率。

略作调整就变成最小批模式

逻辑回归版随机梯度下降分类

对应的最小批模式

习题
Q1

问题1:导入数据,将x分散到0-1范围内,使用公式y=sin(2πx)得到数据Y


Q2

问题2:使用PolynomialFeatures 类建立一个20阶多项式特征,使用线性回归拟合数据,绘制比较结果。注意PolynomialFeatures需要接受一个长为x,高为1的dataframe。

可以对比特征前后数据框情况

Q3

问题3:使用先前多项式特征的数据集进行岭回归与lasso回归,画出图像。
这个图画的非常经典了


图像可以看出来线性回归过拟合,紫色(岭回归)和黄色(lasso回归)都还可以
看看正则化的效果
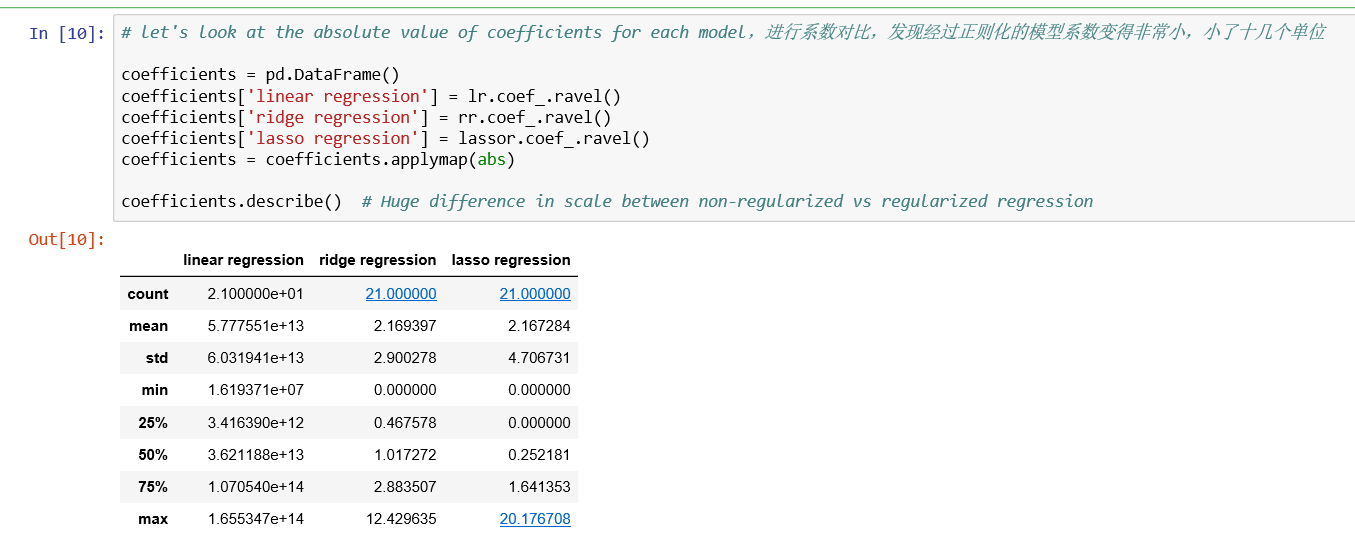
然后是分析20个系数的大小,画图过程相当繁琐。不过图非常简洁,刚开始几个系数较大,但到后面系数非常接近零,贡献降到最低。


Q4

问题4:接下来导入上一个实验的数据集,准备进行接下来的实验。
(1)导入数据,进行one-hot编码

(2)收集浮点类型的数据集,限制斜率

(3)逻辑回归对参数的影响

(4)将打算作为target的SalePrice取出来,准备测试集与训练集
Q5

问题5:写一个rmse函数来对比预测值与实际值,并且返回RMSE。
图像横轴是实际价格,纵轴是预测价格,可以看到两者的比基本接近1:1

Q6

问题6:岭回归使用L2来减小系数大小,这在方差较大的时候回非常有用。问题要求采用如下值作为α的范围。

Q7:

问题7:使用LassoCV和ElasticNetCV对刚才的数据进行交叉验证,比较效果

0.1-0.9范围内的弹性网络

最后绘图比较,发现。。。其实差不多

Q8:

问题8:最后探索一下随机梯度下降,线性模型对缩放非常敏感,同时SGD也是。此外较高的学习率会导致算法发散,过低又影响收敛速度。要求拟合一个随机梯度下降模型,使用三种不同的惩罚措施来交叉验证。注意,在拟合模型钳不要进行缩放。
比较与不使用随机梯度下降的结果。
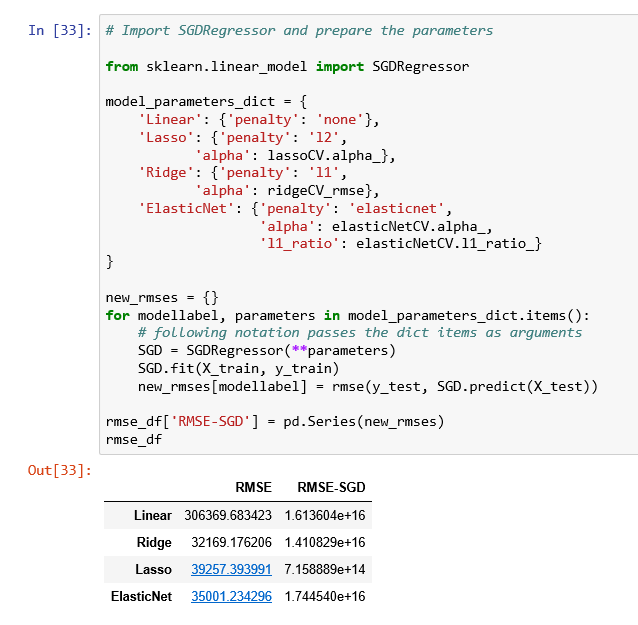
我们发现算法目前错误率高的离谱,我们调整学习率重新比较,发现结果好多了
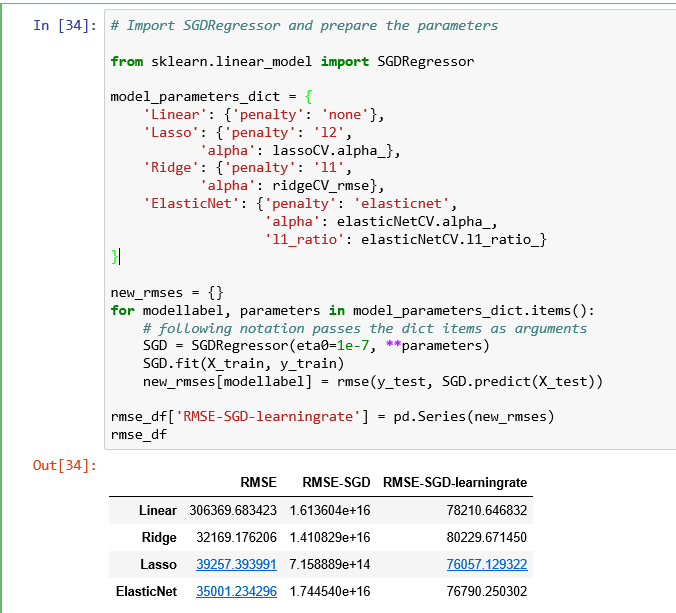
最后对训练数据进行缩放,再次测试效果,不过不要传入eta0
首先不小心传入了eta0

发现误差非常大
那么不传入呢?(默认0.01)

这次效果就相对好一点了。






