债券及衍生品分析计算示例

债券分析

基础计算

日期计算

#先使用to_datetime把某一列的格式转换为日期
df['maturity_date'] = pd.to_datetime(df['maturity_date']) 
df_coupon['b.coupon_obtain_date'] = pd.to_datetime(df_coupon['b.coupon_obtain_date'])

#转化为日期之后的两列可以直接相减，得到相差的天数，但是天数不能直接与数值作比较：
df['date_diff'] = df['maturity_date']-df['value_date']
df['date_diff'] =  df['date_diff'].dt.days

债券利息的计算

债券的计息基准与应计利息的计算（非常详细）：https://mp.weixin.qq.com/s/1j1-LaVTRB-CkuFr1B1log

债券的损益分解（Carry roll-down与PL）

https://zhuanlan.zhihu.com/p/348301609

其它计算

衍生品分析

利率互换计算

【案例一】计算利率互换价值的函数

https://zhuanlan.zhihu.com/p/163607169
假设按照某利率互换条款，某一金融机构同意支付3个月期的SHIBOR，同时收取每年8%的利率（年化利率），名义本金为1亿美元，该互换还有1年时间到期。按照复利计算的3个月、6个月、9个月和12个月的相关贴现率分别是8%、8.3%、8.5%和9%。上一支付日所对应的SHIBOR为8.2%（年化利率）【定盘利率，定下一付息期的利率】。计算该利率互换对于该金融机构的价值。

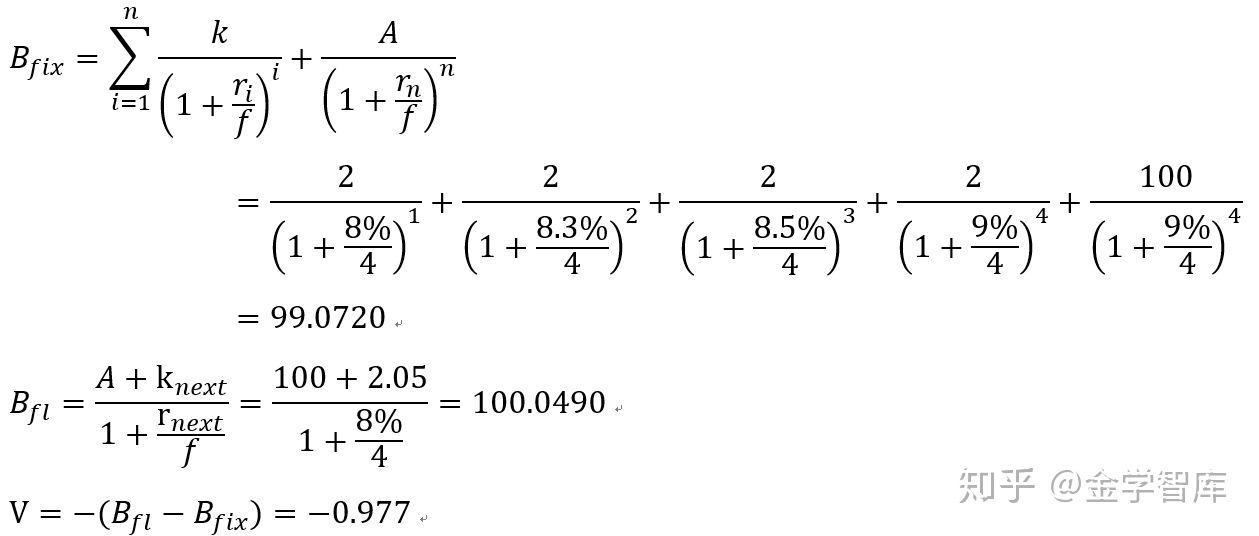
注意该互换1年后到期，因此支付日从现在往后推分别是3个月后，6个月后，9个月和12个月后。该金融机构支浮收固，是互换空头,对于该金融机构来说互换价值为负。

import numpy as np
def int_swap_long(A,k,f,r,n,k_next):
    '''计算利率互换价值的函数；
    A:利率互换中的名义本金金额；
    k:现金流交换日交换的固定利息额；
    f:为年付息频率；
    r：每期的贴现利率；
    n：交换次数；'''
    Bfix=sum(k/(1+r/f)**n)+A/(1+r[-1]/f)**n[-1]
    Bfl=(A+k_next)/(1+r[0]/f)
    return Bfl-Bfix

r1=np.array([0.08,0.083,0.085,0.09])
n1=np.array([1,2,3,4])
V=-int_swap_long(A=100,k=2,f=4,r=r1,n=n1,k_next=2.05) #调用利率互换损益计算函数
print('互换合约的价值为：',round(V,4))

#远期利率的计算
def Rf(R1,R2,T1,T2,n):
    '''定义计算远期利率的函数；
    R1:表示对应期限为T1的零息利率；
    R2:表示对应期限为T2的零息利率；
    T1:表示对应于零息利率R1的期限长度；
    T2:表示对应于零息利率R2的期限长度；
    n：表示年计息频率；'''
    return (((1+R2/n)**(T2*n)/(1+R1/n)**(T1*n))-1)*n  #一般复利

zero_rate=np.array([0.0314,0.0342,0.036,0.0384,0.0402,0.0426,0.0454,0.0495,0.0527,0.0568])
k=2 #付息频率
T_list=np.arange(1,len(zero_rate)+1)/k
R_result=Rf(R1=zero_rate[0:len(zero_rate)-1],R2=zero_rate[1:],T1=T_list[0:len(zero_rate)-1],T2=T_list[1:],n=k)
R_result=np.insert(R_result,0,zero_rate[0]) #第1期利率的即期利率=远期利率
print('远期利率为：',np.round(R_result,4))

#求解利率互换合约定价的固定利率
def fixingrate(A,t,k,R,f):
    '''#求解利率互换合约定价的固定利率的函数
    A:本金；
    t:付息年化时间；
    k：付息频率；
    R：即期利率；
    f：远期利率；'''
    discount=np.zeros(len(t))
    for i in range(len(t)):  #求折现因子
        discount[i]=1/((1+R[i]/(1/k))**(t[i]*k))
    Bfl=A*1/k*sum(f*discount)  #浮动端贴现价格
    from scipy import optimize  #求解固定利率y
    def g(y):
        e=Bfl-A*1/k*sum(y*discount)  #固定端-浮动端=0
        return e
    result=optimize.fsolve(g,0.1)  #猜测固定利率初始值0.1，不断迭代
    return result
        
fixingrate1=fixingrate(A=100,t=T_list,k=2,R=zero_rate,f=R_result)
print('固定利率为：',np.round(fixingrate1,4))

Perfect Bloomberg Price Match of an Interest Rate Swap in Excel by using Dual Bootstrapping

https://blog.deriscope.com/index.php/en/excel-interest-rate-swap-price-dual-bootstrapping-curve

CASE STUDY_DUAL_SWAP_CURVE_VALUATION

https://github.com/domokane/FinancePy-Conference-Notebooks/blob/master/CASE STUDY_DUAL_SWAP_CURVE_VALUATION.ipynb

CASE STUDY EQUITY_VANILLA_OPTION

https://github.com/domokane/FinancePy-Conference-Notebooks/blob/master/CASE_STUDY_EQUITY_VANILLA_OPTION.ipynb

期权计算

QuantLib计算欧式看涨期权

#coding=utf8
import QuantLib as ql
import matplotlib.pyplot as plt
 
# 1.设置期权的五要素以及分红率和期权类型
# 1.1五要素
maturity_date = ql.Date(11, 8, 2017)
spot_price = 9.37
strike_price = 10.00
volatility = 0.20 # the historical vols for a year
risk_free_rate = 0.001
# 1.2分红率
dividend_rate = 0.01
# 1.3期权类型
option_type = ql.Option.Call
 
# 1.4设置日期计算方式与使用地区
day_count = ql.Actual365Fixed()
calendar = ql.UnitedStates()
# 1.5计算期权价格的日期，也就是估值日，我们设为今天
calculation_date = ql.Date(11, 5, 2017)
ql.Settings.instance().evaluationDate = calculation_date
 
# 2.利用上的设置配置一个欧式期权
payoff = ql.PlainVanillaPayoff(option_type, strike_price)
exercise = ql.EuropeanExercise(maturity_date)
# 2.1根据payoff与exercise完成欧式期权的构建
european_option = ql.VanillaOption(payoff, exercise)
 
# 3.构造我们的BSM定价引擎
# 3.1 处理股票当前价格
spot_handle = ql.QuoteHandle(
    ql.SimpleQuote(spot_price)
)
# 3.2 根据之前的无风险利率和日期计算方式，构建利率期限结构
flat_ts = ql.YieldTermStructureHandle(
    ql.FlatForward(calculation_date, risk_free_rate, day_count)
)
# 3.3 设置分红率期限结构
dividend_yield = ql.YieldTermStructureHandle(
    ql.FlatForward(calculation_date, dividend_rate, day_count)
)
# 3.4 设置波动率结构
flat_vol_ts = ql.BlackVolTermStructureHandle(
    ql.BlackConstantVol(calculation_date, calendar, volatility, day_count)
)
# 3.5 构造BSM定价引擎
bsm_process = ql.BlackScholesMertonProcess(spot_handle,
                                           dividend_yield,
                                           flat_ts,
                                           flat_vol_ts)
 
# 4使用BSM定价引擎计算
european_option.setPricingEngine(ql.AnalyticEuropeanEngine(bsm_process))
bs_price = european_option.NPV()
print "The theoretical price is ", bs_price

EQUITY_VANILLA_OPTION

https://github.com/domokane/FinancePy-Conference-Notebooks/blob/master/CASE_STUDY_EQUITY_VANILLA_OPTION.ipynb

利率互换期权计算

https://zhuanlan.zhihu.com/p/126306891

金融量化学习---Python, MySQL, Pandas

导航

公告