Pulp之三：官网上的应用样例（2）-A Set Partitioning Problem (集合划分问题）

Pulp的精髓并不在于单个变量的问题的解决，而在于将约束变量dict化，在有量约束变量的情况下求解。
下面有个例子：https://pythonhosted.org/PuLP/CaseStudies/a_set_partitioning_problem.html
本例来源于PULP的官方文档，本例中使用了pulp.allcombinations()方法,

allcombinations（list, k）: 返回list的所有元素组合，元素个数不超过k

A set partitioning problem determines how the items in one set (S) can be partitioned into smaller subsets.
All items in S must be contained in one and only one partition.

Related problems are （不同的例子）:
1 set packing （集合配置）- all items must be contained in zero or one partitions; 所有项目必须属于某集合或不属于任何集合。
2 set covering （集合覆盖） - all items must be contained in at least one partition.

问题：
有17个客人，有5张桌子，每张桌子最多坐4人。如何分配才能坐满？
如婚礼座位分配问题，一个客人(item）至少坐在某一桌（partition)，不能同时在两桌，一桌可以有多个客人。
In this case study a wedding planner must determine guest seating allocations for a wedding. To model this problem the tables are modelled as the partitions and the guests invited to the wedding are modelled as the elements of S. The wedding planner wishes to maximise the total happiness of all of the tables.

import pulp
max_tables = 5
max_table_size = 4
guests = 'A B C D E F G I J K L M N O P Q R'.split()      # 结果是： ['A', 'B', 'C', 'D', 'E', 'F'... 'R']
# guest1 = 'ABC GHI'.split()    这样分割的结果是 ['ABC', 'GHI']

def happiness(table):
    return abs(ord(table[0]) - ord(table[-1]))
""
    Find the happiness of the table
    - by calculating the maximum distance between the letters
    ord() 函数是 chr() 函数（对于8位的ASCII字符串）或 unichr() 函数（对于Unicode对象）的配对函数，
    它以一个字符（长度为1的字符串）作为参数，返回对应的 ASCII 数值，或者 Unicode 数值
""

                
# 列表化所有的方案
possible_tables = [tuple(c) for c in pulp.allcombinations(guests, max_table_size)]

# 设置变量,这次是一个整数规划的问题，引入01决策变量，在线性规划中设置01变量即，把决策变量的上下限变为01，并设定为整数
x = pulp.LpVariable.dicts('table', possible_tables, lowBound = 0,upBound = 1,cat = pulp.LpInteger)

seating_model = pulp.LpProblem("Wedding Seating Model", pulp.LpMinimize)
seating_model += sum([happiness(table) * x[table] for table in possible_tables])
# x对应一种方案，a对应效益，各个方案的效益总和即为目标函数
# 效益总和 a1x1 + a2x2 + a3x3 + a4x4

#限定决策变量的总数目
# x1+x2+x3...<= 某个值
seating_model += sum([x[table] for table in possible_tables]) <= max_tables,  "Maximum_number_of_tables"                  

# 每个客人只能出席一桌
# 这个语句需要留意一下
for guest in guests:
    seating_model += sum([x[table] for table in possible_tables if guest in table]) == 1, "Must_seat_%s"%guest
		                                                                        
seating_model.solve()

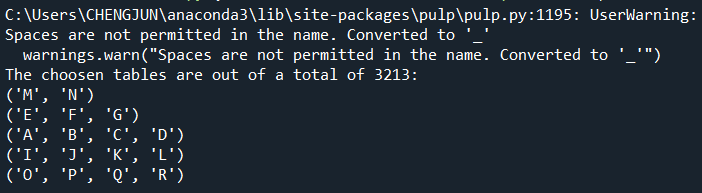
print("The choosen tables are out of a total of %s:"%len(possible_tables))
for table in possible_tables:
    if x[table].value() == 1.0:
        print(table)