卡特兰数的四大公式
卡特兰数
公式一 递归公式
\(h[0]=1\)
\(h[1]=1\)
\(h[n]=h[0]∗h[n−1]+h[1]∗h[n−2]+...+h[n−1]∗h[0] (n>=2)\)
推导:
视频链接:https://www.bilibili.com/video/BV1nE411A7ST?from=search&seid=7193588783915104419
公式二、三 组合数通项公式
\(h[n]=C_{2n}^{n}-C_{2n}^{n-1}\)
\(h[n]=\frac{C_{2n}^{n}}{n+1}\)
推导:
下图中,表示从 (0,0)(0,0) 走到 (n,n)(n,n) 的路径,在绿线及以下表示合法,若触碰红线即不合法。
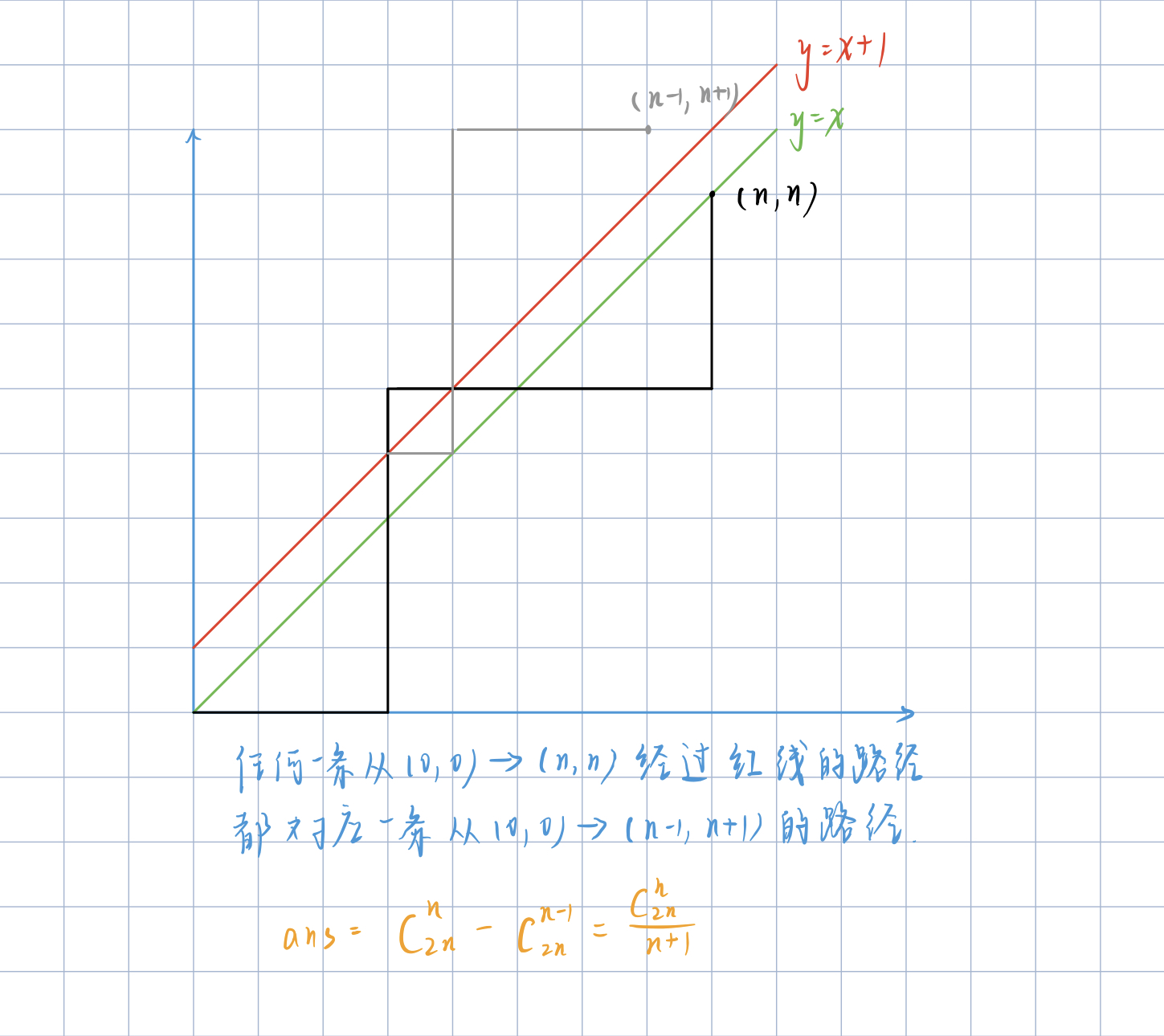
图片来源:https://www.acwing.com/solution/acwing/content/8907/
详细推导过程可参考:https://www.cnblogs.com/zyt1253679098/p/9190217.html
公式四 递推公式
\(h[n+1]=\frac{4n+2}{n+2}h[n]\)
推导:
可参考 https://www.cnblogs.com/zyt1253679098/p/9190217.html



