堆排序

堆排序的原理是利用了完全二叉树的性质

我以这个数组来举例子int arr[]={2,6,4,8,5,3};

这是一颗完全二叉树：

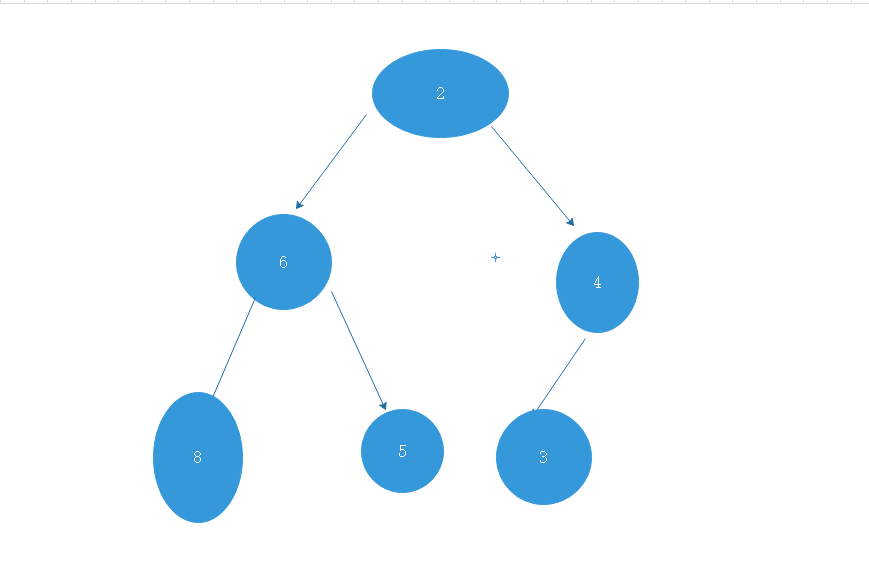
结点的父节点为:(index-1)/2,index是指数组的下标，比如我举个例子值为8的结点在数组中的下标为3，那么它的父节点下标为1，父节点值为6，

结点的左孩子的下标为:index*2+1,index是指数组的下标，比如我举个例子值为6的结点在数组中的下标为1，那么它的左孩子的下标为3，值为8的结点

结点的右孩子的下标为:index*2+2，idnex是指数组的下标，比如我举个例子值为6的结点咋数组的下标为1，那么它的右孩子的下标为4，值为5的结点

知道了这个那就好办了，

第一步把这个完全二叉树调成一个大根堆，何为大根堆，就是任何父节点比左子树或者左孩子，右子树孩子右孩子都要大，

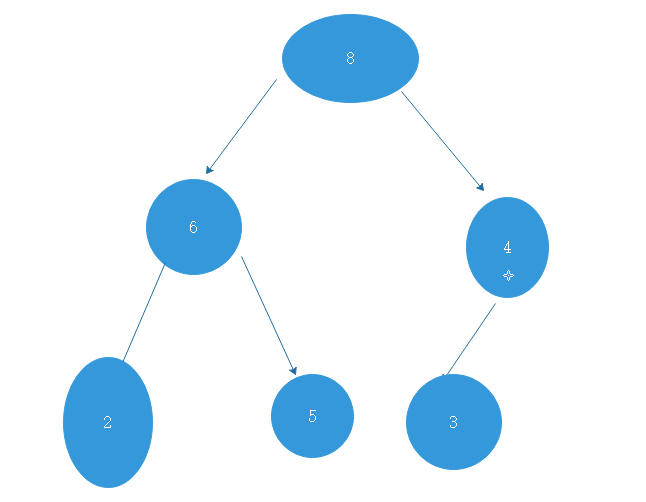
这就是上面哪个例子调成大根堆的完全二叉树，你可以去验证一下不管任何一颗子树的父节点都要比左右孩子要大

那我们来聊聊怎么调成大根堆，具体的在代码中看

/**
	 * 调成大根堆
	 */
	public static void sort(int arr[],int l,int r){
		//每个数组的数都向上调第一个循环意思是数组的每个数都要往上比较，一旦比父节点大就交换
		while(l<=r){
				int parent = (l-1)/2;
				int temp = l;
				//如果这个结点的值比父节点的值要打，就交换，一直往上比较，一旦大就交换
				while(arr[temp]>arr[parent]){
					swap(arr,temp,parent);//这是数组的两个下标的值进行交换
					temp = parent;
					parent = (parent-1)/2;
			}
				l++;
			}
	}

　　调成大根堆，那么你想一下，根结点是不是最大，那么我把根结点和最后一个结点交换，然后让这个大根堆的大小减一，也就是数组的长度减一，这样我不是排好了一个数码！然后在减一后的数组里，此时这个数组不是大根堆，所以我们要用一个函数还使得这个数组还是一个大根堆，然后继续把根结点得值和大根堆范围里最后一个结点交换，直到全部排好!

具体的代码里看

/*
	 * 根结点的值和大根堆范围里的最后一个结点交换，就不是一个大根堆了，这个函数使得
	 * 它变成大根堆
	 */
	public static void heapfy(int arr[],int l,int r){
		int left = l*2+1;//左孩子
		int parent = l;//父节点
		while(left<=r){//这个循环是让根结点的值于左右孩子中的最大值进行比较，如果小于就往下调
						//调完一次后，在于左右孩子比较，知道大于和等于就停止
			int temp = left+1<=r&&arr[left+1]>arr[left]?left+1:left;//返回左右孩子中值最大的下标
			if(arr[temp]<=arr[parent]){//如果父节点等于或者大于左右孩子中最大的一个就退出循环
				break;
			}
			swap(arr,temp,parent);//如果父节点小于左右孩子中的最大的一个，那么就交换
			parent = temp;
			left = temp*2+1;
		}
	}

　　上面这个函数只排好了一个数，所以要有一个循环让这这个函数排好全部的数

public static void finallySort(int arr[],int l,int r){
        sort(arr,l,r);//先调整成大根堆
        swap(arr,l,r);//让根结点于最后一个数交换
        for(int i=r-1;i>0;i--){
            heapfy(arr,0,i);//然后再大根堆范围减一的范围调成成大根堆
            swap(arr,0,i);//调整好了大根堆，继续把根结点与大根堆最后一个结点的值交换
        }
    }

最后来一个完整的代码

public static void finallySort(int arr[],int l,int r){
        sort(arr,l,r);//先调整成大根堆
        swap(arr,l,r);//让根结点于最后一个数交换
        for(int i=r-1;i>0;i--){
            heapfy(arr,0,i);//然后再大根堆范围减一的范围调成成大根堆
            swap(arr,0,i);//调整好了大根堆，继续把根结点与大根堆最后一个结点的值交换
        }
    }
    /**
     * 调成大根堆
     */
    public static void sort(int arr[],int l,int r){
        //每个数组的数都向上调第一个循环意思是数组的每个数都要往上比较，一旦比父节点大就交换
        while(l<=r){
                int parent = (l-1)/2;
                int temp = l;
                //如果这个结点的值比父节点的值要打，就交换，一直往上比较，一旦大就交换
                while(arr[temp]>arr[parent]){
                    swap(arr,temp,parent);//这是数组的两个下标的值进行交换
                    temp = parent;
                    parent = (parent-1)/2;
            }
                l++;
            }
    }
    /*
     * 根结点的值和大根堆范围里的最后一个结点交换，就不是一个大根堆了，这个函数使得
     * 它变成大根堆
     */
    public static void heapfy(int arr[],int l,int r){
        int left = l*2+1;//左孩子
        int parent = l;//父节点
        while(left<=r){//这个循环是让根结点的值于左右孩子中的最大值进行比较，如果小于就往下调
                        //调完一次后，在于左右孩子比较，知道大于和等于就停止
            int temp = left+1<=r&&arr[left+1]>arr[left]?left+1:left;//返回左右孩子中值最大的下标
            if(arr[temp]<=arr[parent]){//如果父节点等于或者大于左右孩子中最大的一个就退出循环
                break;
            }
            swap(arr,temp,parent);//如果父节点小于左右孩子中的最大的一个，那么就交换
            parent = temp;
            left = temp*2+1;
        }
    }
    /**
     * 交换函数
     * @param arr
     * @param l
     * @param r
     */
    public static void swap(int arr[],int l,int r){
        int temp = arr[l];
        arr[l] =arr[r];
        arr[r] =temp;
    }