《线性代数》2. 向量的高级话题

规范化和单位向量

在了解完向量的基础知识后，我们来探讨更多和向量有关的高级话题。首先向量是一个有向线段，由原点指向空间中的某一个点，所以向量除了具有方向之外，还应该具有大小。比如有两个向量 \(\vec{u}\)、\(\vec{w}\)，分别是 \((3, 4)^{T}\)、\((4, 3)^{T}\)，那么它们的长度是多少呢？

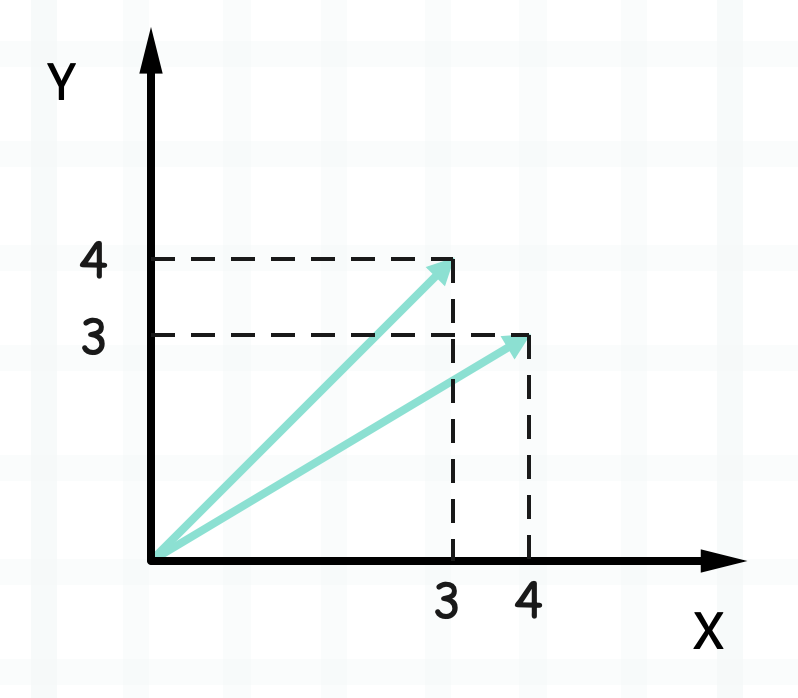
很明显，它们的长度都是 \(5\)。当然在数学领域，向量的长度还有一个更专业的名称，叫向量的模，符号是在向量的周围加上两条双竖线，比如向量 \(\vec{u}\) 的模就是 \(||\vec{u}||\)。

以上是二维向量，如果让你求三维向量的模，肯定也不在话下。比如 \(\vec{u} = (2, 3, 5)^{T}\)，那么它的模 \(||\vec{u}||\) 就等于 \(\sqrt{2^{2} + {3^{2}} + {5^{2}}}\)。如果将向量扩展到 \(n\) 维：

\(\vec{u} = (u_{1}, u_{2}, u_{3}, ..., u_{n})^{T}\)，那么它的模就是 \(\sqrt{u_{1}^{2} + {u_{2}^{2}} + {u_{3}^{2}} + ... + {u_{n}^{2}}}\)，说白了向量的模就是坐标点和原点之间的欧拉距离。

介绍完什么是向量的模，以及如何求之后，我们就可以引入一个新的概念：单位向量（unit vector）。单位向量指的是模为 \(1\) 的向量，所以对于单位向量来说，它的长度已经不重要了，它只表示方向。

对于 \(n\) 维向量 \(\vec{u} = (u_{1}, u_{2}, u_{3}, ..., u_{n})^{T}\)，那么对应的单位向量就是 \(\hat{{u}} = (\frac{u_{1}}{||\vec{u}||}, \frac{u_{2}}{||\vec{u}||}, \frac{u_{3}}{||\vec{u}||}, ..., \frac{u_{n}}{||\vec{u}||})^{T}\)，也就是让向量的在每个维度的分量都除以模。然后单位向量也有专门的表示方式，在符号的上方加上一个类似于 ^ 的符号，就表示该向量是单位向量，并且满足 \(||\hat{u}|| == 1\)。而单位向量 \(\hat{u}\) 和原向量 \(\vec{u}\) 之间的差别仅仅在于它们的长度不同，而方向是一致的，比如向量 \(\vec{u} = (3, 4)^{T}\)，它的单位向量就是 \(\hat{u} = (\frac{3}{5}, \frac{4}{5})^{T}\)。

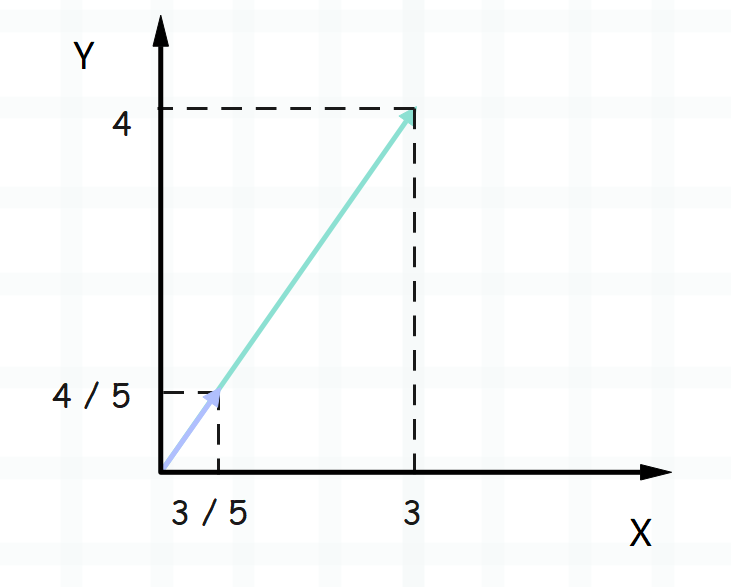
引入单位向量的意义就在于它将向量的模和方向给拆开了，大小可以由向量的模表示，方向可以由向量对应的单位向量表示。如果只关心向量的大小，那么求向量的模即可，如果只关心方向，那么求单位向量即可。而根据向量（\(\vec{u}\)）求出单位向量 \(\hat{u}\) 的过程，就叫做归一化、或者规范化（normalize）。

而且从单位向量的概念上来理解，我们不难发现单位向量有无数个，以二维空间为例，以原点为圆心，半径为 \(1\) 画圆，那么原点到圆上的每一条有向线段都是一个单位向量。如果以三维空间为例，那么以原点为球心，半径为 \(1\) 做一个球，那么球心到球上的每一条有向线段也都是一个单位向量。至于更高维度的向量也是如此。

另外对于二维空间，有两个特殊的单位向量：\(\vec{e_{1}} = (1, 0)\) 和 \(\vec{e_{2}} = (0, 1)\)，因为它们和坐标轴是重合的。同理三维空间有三个特殊的单位向量：\(\vec{e_{1}} = (1, 0, 0)\)、 \(\vec{e_{2}} = (0, 1, 0)\)、\(\vec{e_{3}} = (0, 0, 1)\)。当然这些特殊的单位向量，也叫做标准单位向量，默认使用字母 \(\vec{e}\) 表示。如果拓展到 \(n\) 维的话，那么就有 \(n\) 个标准单位向量。

注意：标准单位向量是很重要的一组向量，由于标准单位向量指向坐标轴的正方向，所以可以说整个坐标系就是由标准单位向量所构建的。

从原理上我们已经介绍了单位向量是什么，那么接下来就用代码来实现它，由于在上一篇文章中我们实现了 Vector 类，那么下面就继续在 Vector 之上添砖加瓦。

import math


class Vector:
    """
    向量
    """

    def __init__(self, values):
        self._values = values

    def __len__(self):
        """返回向量的维度（有多少个元素）"""
        return len(self._values)

    def __repr__(self):
        return f"Vector({self._values})"

    def __str__(self):
        return f"{tuple(self._values)}"

    def __getitem__(self, item):
        """基于索引获取向量的元素"""
        return self._values[item]

    def __add__(self, other):
        if type(other) is not Vector:
            raise TypeError("Vector 只能和 Vector 相加")
        if len(self) != len(other):
            raise TypeError("相加的两个 Vector 的维度必须相同")
        return Vector(
            [self[i] + other[i] for i in range(len(self))]
        )

    def __mul__(self, other):
        if type(other) is not int:
            raise TypeError("Vector 只能和一个整数相乘")
        return Vector(
            [self[i] * other for i in range(len(self))]
        )

    __rmul__ = __mul__

    @classmethod
    def zero(cls, dim: int):
        """构建一个零向量"""
        return cls([0] * dim)

    def __neg__(self):
        """构建一个负向量"""
        return Vector(
            [-self[i] for i in range(len(self))]
        )

    def __eq__(self, other):
        if type(other) is not Vector:
            raise TypeError("Vector 只能和 Vector 进行比较")
        if len(self) != len(other):
            return False
        return all([self[i] == other[i] for i in range(len(self))])

    def norm(self):
        """返回向量的模"""
        return math.sqrt(sum(self[i] ** 2 for i in range(len(self))))

    def normalize(self):
        """返回对应的单位向量"""
        norm = self.norm()  # 如果是 0 向量，那么返回它的单位向量是没有意义的，而且会报错
        if norm < 1e-8:  # 浮点数有误差，不能直接判断 == 0
            raise ValueError("不能获取零向量对应的单位向量")
        return Vector(
            [self[i] / norm for i in range(len(self))]
        )

此时向量的模和单位向量就已经实现了，来测试一下。

from vector import Vector

vec = Vector([3, 4])
print(vec.norm())  # 5.0
print(vec.normalize())  # (0.6, 0.8)
# 单位向量的模是 1
print(vec.normalize().norm())  # 1.0

结果没有问题。

向量的点乘与几何意义

我们之前介绍了两个向量相加，以及一个向量和一个整数相乘，都比较简单，那么两个向量相乘会有什么结果呢？有小伙伴觉得这个还不简单，不就是像下面这样吗？

\(\vec{u} · \vec{w} = \begin{pmatrix} u_{1} \\ u_{2} \\ u_{3} \\ ... \\ u_{n} \\ \end{pmatrix} · \begin{pmatrix} w_{1} \\ w_{2} \\ w_{3} \\ ... \\ w_{n} \\ \end{pmatrix} = \begin{pmatrix} u_{1} · w_{1} \\ u_{2} · w_{2} \\ u_{3} · w_{3} \\ ... \\ u_{n} · w_{n} \\ \end{pmatrix}\)

不好意思，这是错误的，向量的乘法不是这么定义的，至于为什么，后续揭晓。而向量乘法的真正定义如下：

\(\vec{u} · \vec{w} = \begin{pmatrix} u_{1} \\ u_{2} \\ u_{3} \\ ... \\ u_{n} \\ \end{pmatrix} · \begin{pmatrix} w_{1} \\ w_{2} \\ w_{3} \\ ... \\ w_{n} \\ \end{pmatrix} = sum(\begin{pmatrix} u_{1} · w_{1} \\ u_{2} · w_{2} \\ u_{3} · w_{3} \\ ... \\ u_{n} · w_{n} \\ \end{pmatrix}) = u_{1} · w_{1} + u_{2} · w_{2} + u_{3} · w_{3} + ... + u_{n} · w_{n}\)

所以真正的定义相比错误的定义只是多了一个求和操作，因此一个结论就产生了：两个向量相乘的结果不再是向量，而是一个标量，也就是一个数。当然啦，为了方便描述，我们说两个向量相乘，但更严格的说法应该叫两个向量的点乘，或者两个向量的内积。

那么两个向量的点乘为什么要这么定义？背后有什么数学意义呢？其实很简单：

\(\vec{u} · \vec{w} = \begin{pmatrix} u_{1} \\ u_{2} \\ u_{3} \\ ... \\ u_{n} \\ \end{pmatrix} · \begin{pmatrix} w_{1} \\ w_{2} \\ w_{3} \\ ... \\ w_{n} \\ \end{pmatrix} = u_{1} · w_{1} + u_{2} · w_{2} + u_{3} · w_{3} + ... + u_{n} · w_{n} = ||\vec{u}|| · ||\vec{w}|| · cosθ\)

两个向量（\(\vec{u}\)、\(\vec{w}\)）点乘的结果等于：\(\vec{u}\)、\(\vec{w}\) 的每个维度上的分量分别相乘，然后再相加，同时它也等于：\(\vec{u}\)、\(\vec{w}\) 的模相乘之后再乘上两者夹角的余弦值。下面我们就以二维平面为例，来证明这个结论。不过证明之前，需要补充一个知识点：向量的减法。

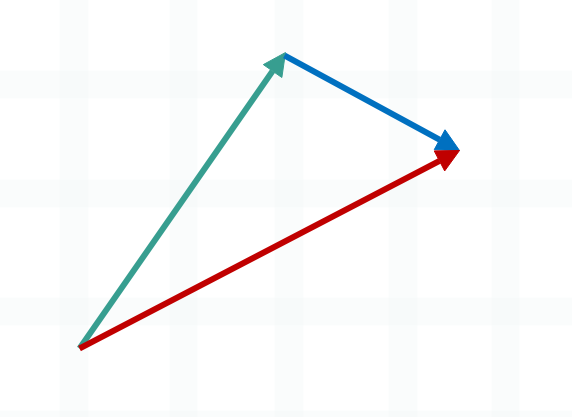
注：向量的尾巴（没有箭头）是向量的起始点，向量的箭头是向量的结束点。

如果将绿色的线段记作 \(\vec{u}\)，蓝色的线段记作 \(\vec{w}\)，那么红色的线段等于多少呢？毫无疑问，等于 \(\vec{u} + \vec{w}\)。这个我们在高中的时候学过，如果多个向量像上图一样满足首尾相连，那么第一个向量的起始点和最后一个向量的结束点之间的连线，就等于所有向量之和。然后我们还将绿色的线段记作 \(\vec{u}\)，但是将红色的线段记作 \(\vec{w}\)，那么此时蓝色的线段等于多少呢？很明显，它等于红色线段对应的向量，减去绿色线段对应的向量，也就是 \(\vec{w} - \vec{u}\)。

和加法一样，两个向量相减等于每一个维度上的分量进行相减，并且返回的也是向量。

然后还要补充一个余弦定理，假设有一个三角形，三条边记作：a、b、c，并且 a 的对角为 \(θ_{a}\)，b 的对角为 \(θ_{b}\)，c 的对角为 \(θ_{c}\)。

那么结论如下：

\(a^{2} = b^{2} + c ^ {2} - 2·b·c·cosθ_{a}\)
\(b^{2} = a^{2} + c ^ {2} - 2·a·c·cosθ_{b}\)
\(c^{2} = a^{2} + b^{2} - 2·a·b·cosθ_{c}\)

好了，补充完向量的减法和余弦定理之后，我们在二维空间中证明上面那个结论：

\(\vec{u} · \vec{w} = \begin{pmatrix} u_{1} \\ u_{2} \\ \end{pmatrix} · \begin{pmatrix} w_{1} \\ w_{2} \\ \end{pmatrix} = u_{1} · w_{1} + u_{2} · w_{2} = ||\vec{u}|| · ||\vec{w}|| · cosθ\)

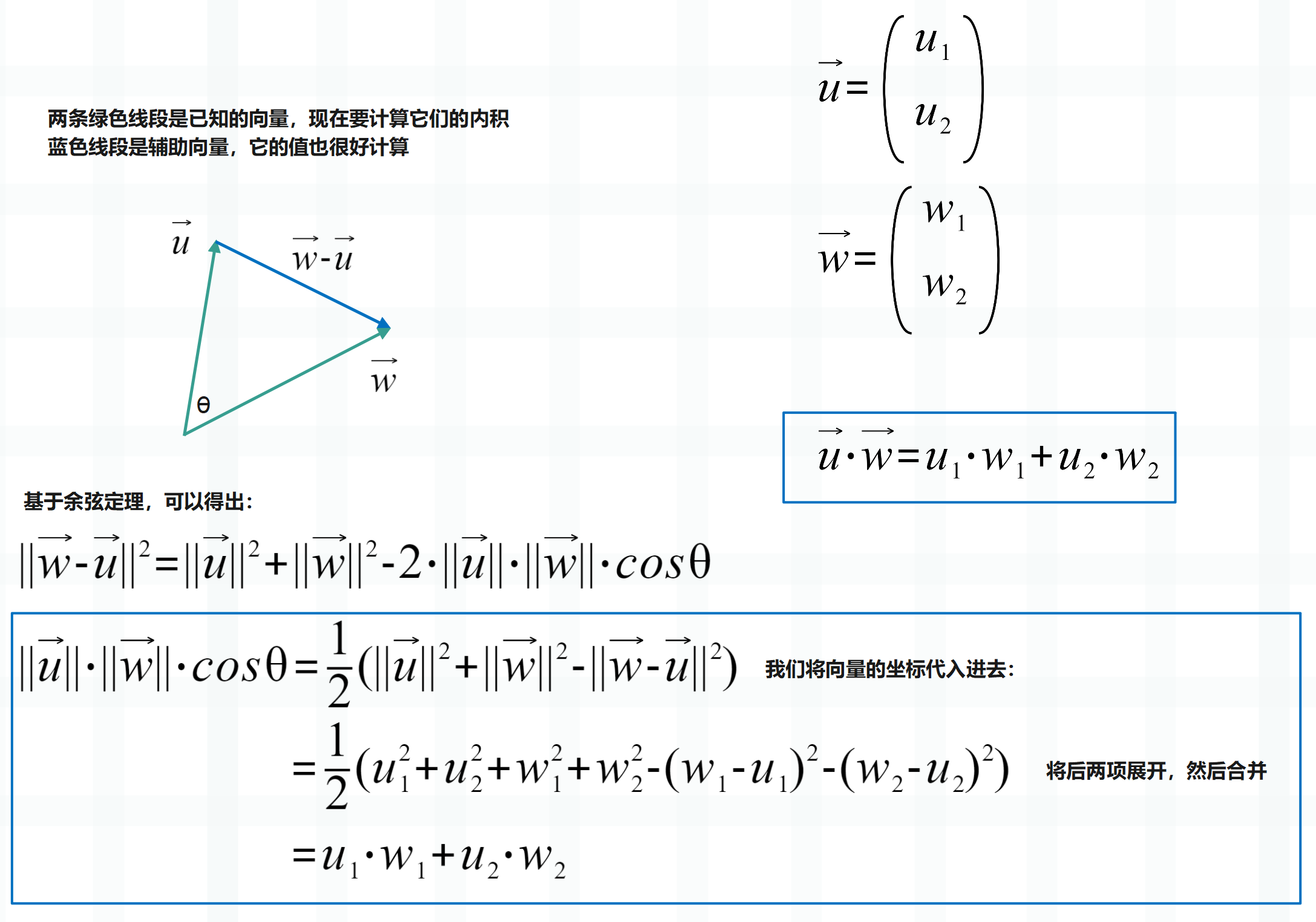
基于已有的余弦定理，我们就证明了这个结论：\(\vec{u} · \vec{w} = \begin{pmatrix} u_{1} \\ u_{2} \\ \end{pmatrix} · \begin{pmatrix} w_{1} \\ w_{2} \\ \end{pmatrix} = u_{1} · w_{1} + u_{2} · w_{2} = ||\vec{u}|| · ||\vec{w}|| · cosθ\)，这便是向量的点乘（内积）。

当然扩展到 \(n\) 维也是成立的：\(\vec{u} · \vec{w} = \begin{pmatrix} u_{1} \\ u_{2} \\ u_{3} \\ ... \\ u_{n} \\ \end{pmatrix} · \begin{pmatrix} w_{1} \\ w_{2} \\ w_{3} \\ ... \\ w_{n} \\ \end{pmatrix} = u_{1} · w_{1} + u_{2} · w_{2} + u_{3} · w_{3} + ... + u_{n} · w_{n} = ||\vec{u}|| · ||\vec{w}|| · cosθ\)，有兴趣可以自己验证一下。

编程实现向量点乘

这里我需要事先说明一下，乘法在计算机中就表示单纯的乘法，即使在 Numpy 中也是如此。

import numpy as np

arr1 = np.array([1, 2, 3])
arr2 = np.array([11, 22, 33])
# 让每个元素分别进行相乘
print(arr1 * arr2)  # [11 44 99]

如果你想实现向量的点乘，在 Python 里面你应该使用 @ 符号。也就是说：@ 才是向量的点乘，而 * 始终表示普通的乘法。

import numpy as np

arr1 = np.array([1, 2, 3])
arr2 = np.array([11, 22, 33])
print(arr1 * arr2)  # [11 44 99]

# 1 * 11 + 2 * 22 + 3 * 33
print(arr1 @ arr2)  # 154

而 @ 操作符对应的魔法方法是 __matmul__，所以我们需要重载 Vector 的 __matmul__ 方法。这里的 mat 表示矩阵的意思，也就是矩阵乘法，而向量可以看作是一维矩阵。

import math


class Vector:
    """
    向量
    """

    def __init__(self, values):
        self._values = values

    def __len__(self):
        """返回向量的维度（有多少个元素）"""
        return len(self._values)

    def __repr__(self):
        return f"Vector({self._values})"

    def __str__(self):
        return f"{tuple(self._values)}"

    def __getitem__(self, item):
        """基于索引获取向量的元素"""
        return self._values[item]

    def __add__(self, other):
        if type(other) is not Vector:
            raise TypeError("Vector 只能和 Vector 相加")
        if len(self) != len(other):
            raise TypeError("相加的两个 Vector 的维度必须相同")
        return Vector(
            [self[i] + other[i] for i in range(len(self))]
        )

    def __mul__(self, other):
        if type(other) is not int:
            raise TypeError("Vector 只能和一个整数相乘")
        return Vector(
            [self[i] * other for i in range(len(self))]
        )

    __rmul__ = __mul__

    @classmethod
    def zero(cls, dim: int):
        """构建一个零向量"""
        return cls([0] * dim)

    def __neg__(self):
        """构建一个负向量"""
        return Vector(
            [-self[i] for i in range(len(self))]
        )

    def __eq__(self, other):
        if type(other) is not Vector:
            raise TypeError("Vector 只能和 Vector 进行比较")
        if len(self) != len(other):
            return False
        return all([self[i] == other[i] for i in range(len(self))])

    def norm(self):
        """返回向量的模"""
        return math.sqrt(sum(self[i] ** 2 for i in range(len(self))))

    def normalize(self):
        """返回对应的单位向量"""
        norm = self.norm()  # 如果是 0 向量，那么返回它的单位向量是没有意义的，而且会报错
        if norm < 1e-8:  # 浮点数有误差，不能直接判断 == 0
            raise ValueError("不能获取零向量对应的单位向量")
        return Vector(
            [self[i] / norm for i in range(len(self))]
        )
    
    def __matmul__(self, other):
        if type(other) is not Vector:
            raise TypeError("Vector 只能和 Vector 进行比较")
        if len(self) != len(other):
            raise TypeError("点乘的两个 Vector 的维度必须相同")
        return sum(self[i] * other[i] for i in range(len(self)))

实现完毕，我们来测试一下：

from vector import Vector

vec1 = Vector([1, 2, 3])
vec2 = Vector([11, 22, 33])
print(vec1 @ vec2)  # 154

结果没有问题，非常简单。

向量点乘的应用

基于向量的点乘公式 \(\vec{u} · \vec{w} = u_{1} · w_{1} + u_{2} · w_{2} + u_{3} · w_{3} + ... + u_{n} · w_{n} = ||\vec{u}|| · ||\vec{w}|| · cosθ\)，我们可以很容易求出两个向量的夹角：\(cosθ = \frac{\vec{u} · \vec{w}}{||\vec{u}|| · ||\vec{w}||}\)。

如果 \(θ\) 等于 \(90°\)，那么这两个向量点乘的结果就是 \(0\)；
反之，如果两个向量点乘的结果是 \(0\)，那么这两个向量互相垂直（夹角为 \(90°\)）；

而且我们也能够推出：

如果 \(\vec{u} · \vec{w} > 0\)，那么两个向量之间夹角为锐角；
如果 \(\vec{u} · \vec{w} < 0\)，那么两个向量之间夹角为钝角；
如果 \(\vec{u} · \vec{w} = 0\)，那么两个向量之间夹角为直角，比如标准单位向量点乘的结果就是 0。并且无论维度是多少，标准单位向量永远是两两垂直的；

然后向量点乘还可以用在推荐系统当中，比如你看了某部电影之后觉得非常喜欢，那么如果再有与之相似的电影，系统就会推荐给你。当然电商系统里的商品也是如此，而在这个策略背后，就是如何判断两个商品的相似度呢？答案就是向量的点乘。首先基于商品的特征，可以抽象成高维空间的一个向量，那么我们只需要看两个向量的夹角即可。

如果为锐角，那么两个商品是具有一定相似度的，并且角度越小，相似度越高
如果为直角，那么两个商品是不具有相似度，彼此无关
如果为钝角，那么两个商品的特征是相反的

在 Numpy 中如何使用向量

说到科学计算，就不得不说 Numpy，它是奠定 Python 数据科学的最大功臣。那么在 Numpy 中，我们如何使用向量呢？

import numpy as np

# 在 numpy 中我们一般会创建一维数组来表示向量
# 如果是矩阵，那么就用多维数组来表示
vec1 = np.array([1, 2, 3])
vec2 = np.array([2, 3, 4])

# 向量的加法
print(vec1 + vec2)  # [3 5 7]
# 向量的减法
print(vec1 - vec2)  # [-1 -1 -1]
# 向量和一个标量相乘
print(vec1 * 3)  # [3 6 9]
# 向量的乘法（每个元素相乘，得到的还是向量）
print(vec1 * vec2)  # [ 2  6 12]
# 向量的点乘
print(vec1 @ vec2)  # 20

然后 np 下面有一个子模块 linalg，里面包含了大量和线性代数相关的方法，因为 linalg 就是线性代数的缩写。

import numpy as np

vec = np.array([1, 2, 3])
# 计算向量的模
print(np.linalg.norm(vec))
"""
3.7416573867739413
"""
# 计算单位向量，numpy 并没有直接提供单位向量，需要我们手动做一下除法
print(vec / np.linalg.norm(vec))
"""
[0.26726124 0.53452248 0.80178373]
"""
# 单位向量的模是 1
print(np.linalg.norm(vec / np.linalg.norm(vec)))  # 1.0

另外计算单位向量的时候，要确保原向量不是零向量，这一点需要由使用者保证。

posted @ 2023-08-26 18:44 古明地盆阅读(372) 评论(0) 编辑收藏举报

刷新页面返回顶部

来自东方地灵殿的小提琴手

愿时间能带走痛苦