一文让你明白什么是泰勒展开式?
有一位数学家叫泰勒,某天看到一个函数 \(y = cosx\),瞬间眉头一皱,心里面不断犯嘀咕。有些函数它就是很恶心,本来这些函数具备很优秀的品质(可以轻松地无限次求导),但如果代入数值计算的话就比较困难了。比如这里的 \(f(x) = cosx\),在没有计算机的年代,很难计算出 \(x = 2\) 时 \(f(x)\) 的值。
为避免这种尴尬局面,泰勒就开始想:我能不能找到另一条曲线 \(g(x)\),它和 \(f(x)\) 无限相似,但相比之下却能更简单地进行求值呢?所以面对 \(f(x) = cosx\),泰勒的目的是仿造一条一模一样的曲线,从而避免余弦计算。
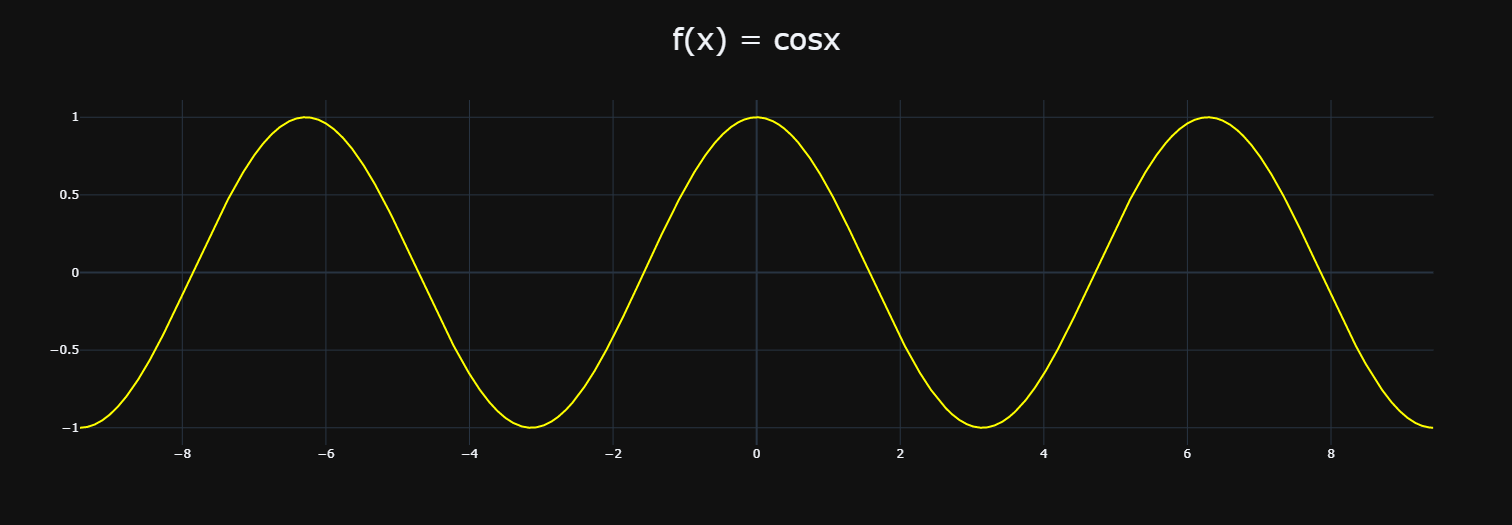
想要复制这段曲线,首先得找一个切入点,可以是这条曲线最左端的点,也可以是最右端的点,亦或是这条线上任何一点,而泰勒选择了 \((0, 1)\)。由于这段曲线经过 \((0, 1)\) 这个点,那么仿造的第一步就是让仿造的曲线也经过这个点。并且仿造的曲线也要能够很轻松地根据 x 进行求值,否则仿造就没有意义了。
经过 \((0, 1)\) 的曲线有很多,比如 \(f(x) = x^2 + 1\),但它们仅仅是经过了 \((0, 1)\) 这个点,至于其它的部分则和 \(f(x) = cosx\) 没有任何相似之处。所以泰勒不仅要保证仿造的曲线过 \((0, 1)\) 点,还要保证在这一点导数和原曲线也是相等的,导数相同意味着变化趋势相同。
还没结束,起始点相同,变化趋势相同,还要考虑曲线的凸凹性。我们知道表征曲线的凸凹性的参数被称为"导数的导数",所以还要保证导数的导数相等。于是泰勒开始动手计算了,首先他知道自己要仿照一段曲线,从 \((0, 1)\) 入手,要保证:
- 初始值相同:\(g(0) = f(0)\)
- x = 0 处的一阶导相同:\(g'(0) = f'(0)\)
- x = 0 处的二阶导相同:\(g''(0) = f''(0)\)
- ............
- x = 0 处的 n 阶导相同:\(g^{'''...}(0) = f^{'''...}(0)\),光有一阶和二阶是不够的
这时候,泰勒思考了两个问题:
1)余弦函数能够无限次求导,为了让这两条曲线无限相似,自己仿造出来的 g(x) 必须也能够无限次求导,那 g(x) 得是什么样类型的函数呢?2)实际操作过程中,肯定不能无限次求导,只需要求几次,就可以达到想要的精度。那么,实际过程中应该求几次比较合适呢?
综合考虑这两个问题以后,泰勒给出了一个比较折中的方法:令 \(g(x)\) 为多项式,多项式能求几次导数取决于多项式本身。比如五次多项式 \(g(x) = ax^5 + bx^4 + cx^3 + dx^2 + ex + f\) 能求 5 次导,再求就是 0 了,所以几次多项式就能求几次导数。
所以泰勒就开始使用多项式来模拟了,很明显为了发现规律,要从最低次开始,所以选择了 \(g(x) = 1\)。
由于 \(cos'x = -sinx,sin'x = cosx\),所以 \(cosx\) 在 x = 0 处的一阶导数为 0(\(-sin0\))、二阶导数为 -1(\(-cos0\))、三阶导数为 0(\(sin0\))、四阶导数为 1(\(cos0\)),以此类推。
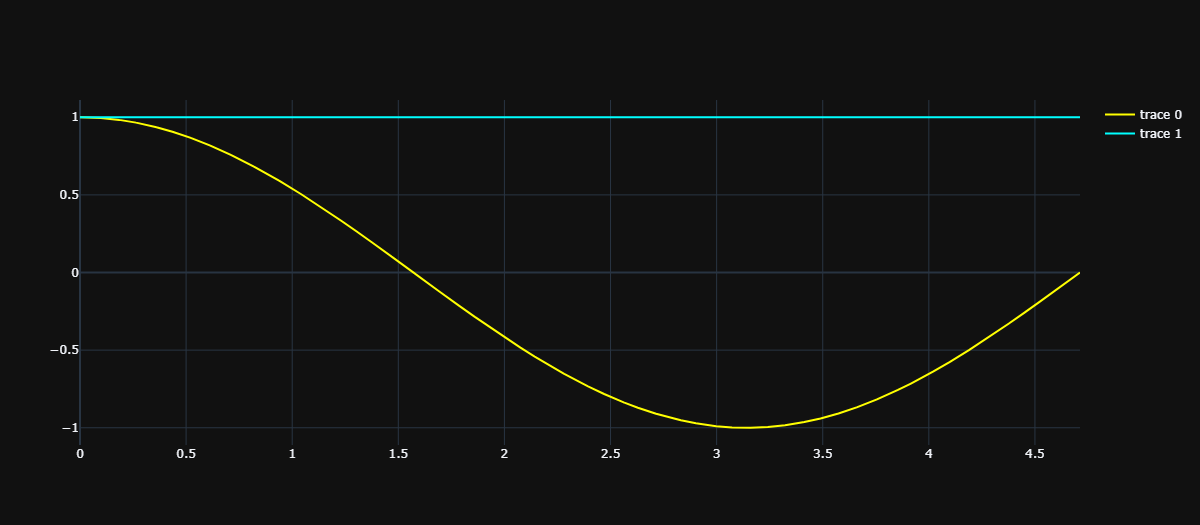
除了都经过 \((0, 1)\)、以及在 x=0 处的导数均为 0 之外,没有任何相似之处,那么下面要满足二阶导也相等。所以泰勒选择了 \(g(x) = -{\frac 1 2}x^{2} + 1\):
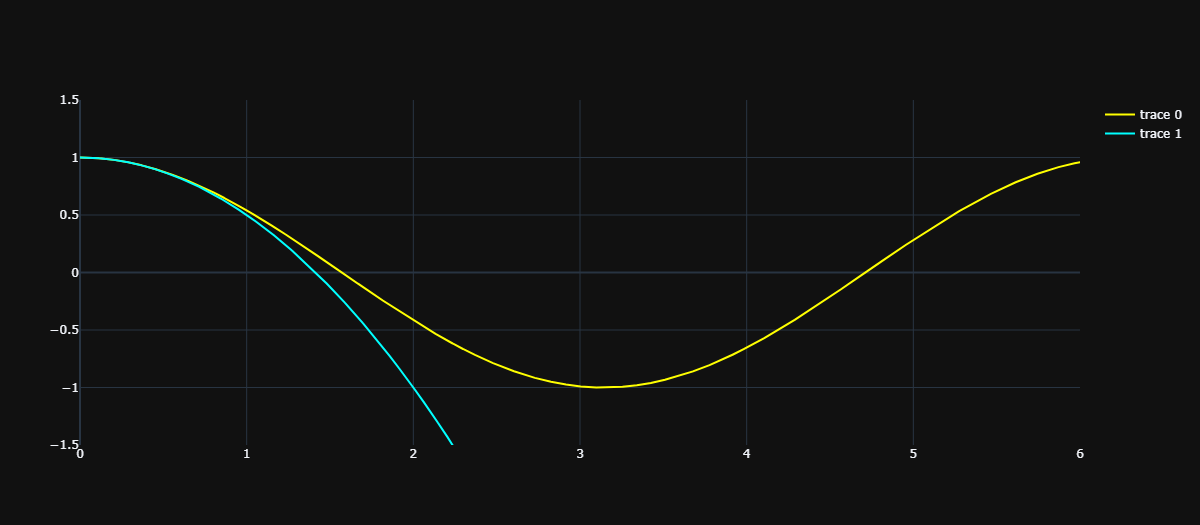
我们看到在 \((0, 1)\) 附近的一个小范围内,二者拟合的比较好。那么多项式的阶数再提高一些,也就是保证更高阶的导数相等,比如 4 介导。于是泰勒经过一番计算之后,找到了一阶到四阶都和 \(cosx\) 相等的多项式:\(g(x) = {\frac 1 {24}}x^{4} - {\frac 1 2}x^{2} + 1\)。
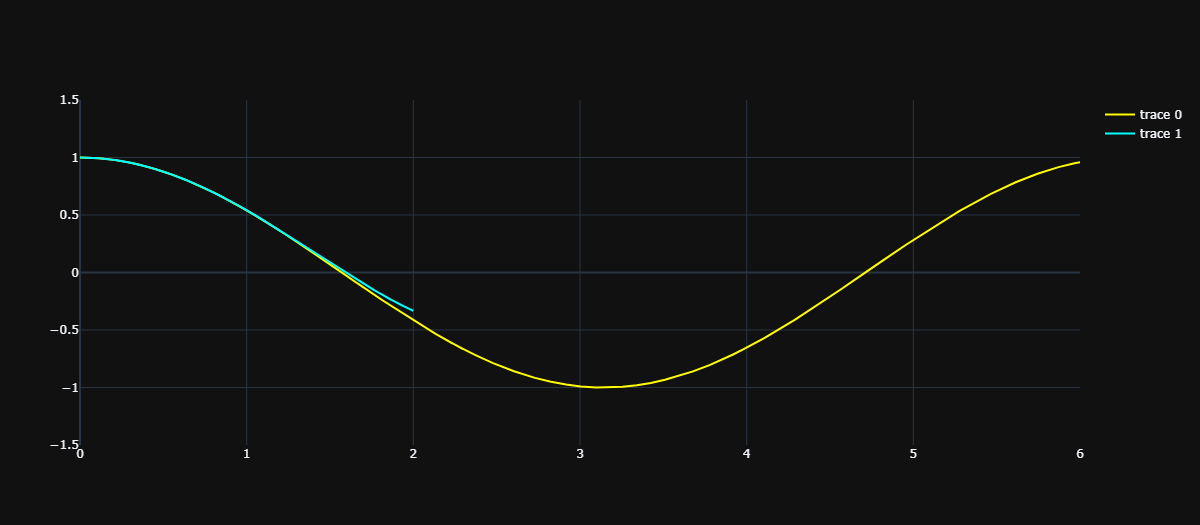
可以看到两条曲线拟合的程度变高了,因此不光是泰勒,相信我们也可以想到,如果继续提高多项式的阶数,只要使得它们在 n 次求导之后的导数都相同,那么无穷高阶后,两条曲线一定是无限相似的。
但问题是泰勒当时没有计算机,只能手算,和我们一样算到四阶就算不动了,他就开始发呆:我在哪?我是谁?我在做什么?哦对了,是为了找一个多项式,方便计算 cos2。但问题他是从 \(x=0\) 开始算的,距离 \(x=2\) 还有一段距离,必须得继续算才能将两曲线重合的范围辐射到 \(x=2\) 处。站在上帝视角的我们从上图中可以看到,两条曲线在 \(x=2\) 处还是没有拟合的,如果想拟合,那么至少需要再找一个 5 阶多项式,保证让它们的五阶导也相同。
但很明显它算不下去了,咋办呢?突然他一拍脑门,恍然大悟,既然我选的点离着我想要的点比较远,那我为啥不直接选个近的点呢,反正能从这条曲线上任何一个点作为切入,开始仿造,近了能省很多计算量啊。比如上图是从 \((0, 1)\) 切入的,虽然计算 \(x=2\) 还有误差,但计算 \(x=1\) 是可以的,因为 \(x=1\) 离选择的点要更近。
x = 1
print(np.cos(x)) # 0.5403023058681398
print(x ** 4 / 24 - x ** 2 / 2 +1) # 0.5416666666666667
保留两位小数的话,显然是相等的。于是为了计算 \(cos2\) 的泰勒,不从 \((0, 1)\) 开始切入了,他选择了从 \(({\frac π 2}, 1)\)、也就是 \(x={\frac π 2}\) 处开始切入。
所以这就是泰勒展开式,相信你已经理解了。本质上就是"仿造",即:把一个三角函数、指数函数、亦或是其它比较难缠的函数用多项式替换掉。也就是说,有一个原函数 \(f(x)\),再造一个图像与之相似的函数 \(g(x)\),为了保证两者图像相似,只需要保证在某一点的初始值、以及一阶导函数的值、二阶导函数的值、......、n 阶导函数的值相等即可。只要能保证这一点,那么两个函数的图像就是相似的。
但是泰勒算到四阶之后就不想算了,所以他想把这种计算过程推广到 n 阶,算出一个代数式,然后直接代数就可以了,于是就有了下面的推导过程。
首先要在原曲线 \(f(x)\) 上选择一个点,为了方便就选 \((0, f(0))\),而仿造的曲线是一个能求 n 介导的多项式,所以它的最高次数一定也是 n,所以其解析式肯定是下面这种形式:
\(g(x) = a_{0} +a_{1}x + a_{2}x^{2} + a_{3}x^{3}...... + a_{n}x^{n}\)
首先要保证初始值相同,由于我们选择的是 \((0, f(0))\),那么一定有 \(f(0) = g(0) = a_{0}\)。然后保证 n 阶导数相等,即\(g^{n}(0) = f^{n}(0)\),因为对 \(g(x)\) 求 n 阶导数时,只有最后一项非零值,所以我们只看最后一项。
- \(a_{n}x^{n}\) 求一阶导,得到 \(na_{n}x^{n-1}\);
- \(a_{n}x^{n}\) 求二阶导,得到 \(n(n-1)a_{n}x^{n-2}\);
- \(a_{n}x^{n}\) 求三阶导,得到 \(n(n-1)(n-2)a_{n}x^{n-3}\);
- \(a_{n}x^{n}\) 求 n 阶导,得到 \(n(n-1)(n-2)··· 2*1*a_{n}x^{0}\),即 \(n!a_{n}\);
所以 \(g^{n}(0) = n!a_{n} = f^{n}(0)\),由此得出 \(a_{n} = {\frac {f^{n}(0)} {n!}}\)。然后根据规律,对 \(g(x)\) 中的 \({a_{i}}\) 进行替换,即可得出:
\(g(x) = g(0) + {\frac {f^{1}(0)} {1!}}x + {\frac {f^{2}(0)} {2!}}x^{2} + {\frac {f^{3}(0)} {3!}}x^{3}...... + {\frac {f^{n}(0)} {n!}}x^{n}\)
以上就是整个推导过程,还是很简单的,但是到这里泰勒又想到了一个问题,那就是不一定非要从 \(x=0\) 的位置切入,也可以从 \(x=x_{0}\) 处开始。只要将 0 换成 \(x_{0}\) 再按照上面的流程重来一遍,即可得到如下结果:
\(g(x) = g(x_{0}) + {\frac {f^{1}(x_{0})} {1!}}(x-x_{0}) + {\frac {f^{2}(x_{0})} {2!}}(x-x_{0})^{2} + {\frac {f^{3}(x_{0})} {3!}}(x-x_{0})^{3}...... + {\frac {f^{n}(x_{0})} {n!}}(x-x_{0})^{n}\)
写到这里,泰勒长舒一口气,写下结论:有一条解析式很恶心的曲线 \(f(x)\),那么可以用多项式仿照一条曲线 \(g(x)\),并且满足:
\(f(x) ≈ g(x) = g(x_{0}) + {\frac {f^{1}(x_{0})} {1!}}(x-x_{0}) + {\frac {f^{2}(x_{0})} {2!}}(x-x_{0})^{2} + {\frac {f^{3}(x_{0})} {3!}}(x-x_{0})^{3}...... + {\frac {f^{n}(x_{0})} {n!}}(x-x_{0})^{n}\)
泰勒指出:在实际操作过程中,可根据精度要求选择 n 值,只要 n 不是正无穷,那么一定要保留上式中的约等号。若想去掉约等号,需要写成下面形式:
\(f(x) = g(x) = g(x_{0}) + {\frac {f^{1}(x_{0})} {1!}}(x-x_{0}) + {\frac {f^{2}(x_{0})} {2!}}(x-x_{0})^{2} + {\frac {f^{3}(x_{0})} {3!}}(x-x_{0})^{3}...... + {\frac {f^{n}(x_{0})} {n!}}(x-x_{0})^{n} + ······\)
以上就是泰勒展开式,只要理解了背后的思想还是很好推理的。
那么根据泰勒展开式,像 \(e^{x}\)、\(sin(x)\)、\(cos(x)\) 这些函数我们可以很轻松地用多项式进行替代,举个栗子:
- 当 \(x_{0}\) 取 \(0\) 时, \(e^{x} = 1 + x + {\frac 1 {2!}}x^{2}+{\frac 1 {3!}}x^{3}+···\)
- 当 \(x_{0}\) 取 \(0\) 时,\(sinx = x - {\frac 1 {3!}}x^{3}+{\frac 1 {5!}}x^{5}+···\);
- 当 \(x_{0}\) 取 \(0\) 时,\(cosx = 1-{\frac 1 {2!}}x^{2}+{\frac 1 {4!}}x^{4}···\)
以上也被成为麦克劳林公式,当然麦克劳林公式只是泰勒展开式在 \(x_{0}\) 取 \(0\) 时的一种特殊形式。但这不是关键,如果将 \(e^{x}\) 里面的 \(x\) 换成 \(ix\),其中 \(i\) 为虚数,那么就有:
\(e^{ix} = 1 + ix -{\frac 1 {2!}}x^{2}-i{\frac 1 {3!}}x^{3}+{\frac 1 {4!}}x^{4}+i{\frac 1 {5!}}x^{5}+···= cosx + i*sinx\)
所以我们就得到了著名的公式,欧拉公式:\(e^{ix} = cosx + i*sinx\),如果将 \(x\) 换成 \(π\),那么便可得到一个最美的式子:\(e^{iπ} + 1 = 0\)。这个式子它美在哪儿呢?我们看到 \(e\) 是自然对数的底数、\(i\) 是虚数、\(pi\) 是无理数、\(1\) 是有理数,这几个看起来毫无关系的数组合起来,相加居然等于 \(0\)。
后续
但是故事还没有结束,泰勒虽然留下了这个式子,但是他没有告诉你到底该求导几次,所以便有了一帮人帮他擦屁股。
第一个帮他擦屁股的人叫佩亚诺,泰勒只将展开式写到了第 n 项,佩亚诺将省略号的部分给补全了。
\(f(x) = g(x) = g(x_{0}) + {\frac {f^{1}(x_{0})} {1!}}(x-x_{0}) + {\frac {f^{2}(x_{0})} {2!}}(x-x_{0})^{2} + {\frac {f^{3}(x_{0})} {3!}}(x-x_{0})^{3}+··· + {\frac {f^{n}(x_{0})} {n!}}(x-x_{0})^{n} + {\frac {f^{(n+1)}(x_{0})} {(n+1)!}}(x-x_{0})^{n+1}+···+{\frac {f^{(∞)}(x_{0})} {∞!}}(x-x_{0})^{∞}\)
从第 n + 1 项开始的部分就是误差,于是佩亚诺开始思考,怎么能让误差无限趋近于 0。因为一旦误差趋近于 0 了,那么就可以省去了,泰勒展开只需要展开到 n 阶就可以了。
于是这个小机灵鬼发现只要让 \(x\) 趋近于 \(x_{0}\) 不就行了吗?看到这,是不是一脸无语。总结一下皮亚诺的思路:首先它把泰勒展开式中没写出来的部分给补全,然后将这些项之和称为误差项,之后他想把误差项变成 0。于是对式子做了一些变换,最后发现只有当 \(x\) 趋近于 \(x_{0}\) 的时候,误差项才为 0。
说实话,感觉像是说了一堆废话,但是为了纪念他,将这些误差项称为佩亚诺余项。
下面第二个擦屁股的人登场了,这个人叫拉格朗日,我们从头说起。有一天拉格朗日闲得无聊,思考了一个特别简单的问题:一辆车从 \(S_{1}\) 处走到了 \(S_{2}\) 处,用了时间 \(t\),那么这辆车的平均速度就是 \(v={\frac {S_{1}-S_{2}} t}\)。
但车不是匀速直线运动,那么肯定有一个时刻的瞬时速度是小于 \(v\) 的,同理也会有一个时刻的瞬时速度是大于 \(v\) 的。由于车的速度不能突变,那么从小于 \(v\) 到大于 \(v\) 这一过程,肯定有一个瞬间,车的速度等于 \(v\)。
即使没有听过拉格朗日,相信也能想明白这个问题,但拉格朗日的牛逼之处在于,能把生活中的小事翻译成数学语言,并画成了图像。

把上面这个简单的问题用数学语言描述出来的话,就得到了拉格朗日中值定理:有一个函数 \(S(t)\),如果在 \(t_{1}\) 到 \(t_{2}\) 范围连续且可导,那么有:\({\frac {S(t_{2}) - S(t_{1})} {t_{2} - t{1}}} = S'(t)\),其中 \(t∈[t_{1}, t_{2}]\)。
后来拉格朗日的中值定理被柯西看到了,柯西天生对于算式敏感。柯西认为,纵坐标是横坐标的函数,那我也可以把横坐标写成一个函数啊,于是他提出了柯西中值定理:
\({\frac {S(t_{2}) - S(t_{1})} {T(t_{2}) - T(t_{1})}} = {\frac {S'(t) } {T'(t)}}\)
拉格朗日听说了这事之后,心里愤愤不平,又觉得很可惜。明明是自己的思路,明明是我先的,结果差这么一步,就让柯西捡便宜了,不过柯西确实说的有道理,这件事给拉格朗日留下了很深的心理阴影。
接下来,拉格朗日开始思考泰勒级数的误差问题,他同佩亚诺一样,也只考虑误差部分。先把误差项写出来,记为 \(R(x)\)。
\(R(x) = {\frac {f^{(n+1)}(x_{0})} {(n+1)!}}(x-x_{0})^{n+1}+{\frac {f^{(n+2)}(x_{0})} {(n+2)!}}(x-x_{0})^{n+2}+···+{\frac {f^{(∞)}(x_{0})} {∞!}}(x-x_{0})^{∞}\)。
显然 \(R(x_{0}) = 0\)。
误差项 \(R(x)\) 中的每一项都是两数的乘积,假如是你,你肯定是想两边同时除掉一个 \((x - x_{0})^{n+1}\) 对吧。为了简单,我们将其记作 \(T(x)\)。

所以除过之后,就变成了:

等等,这一串东西怎么看着如此眼熟?咦,这不是柯西老哥推广的我的中值定理么?剩下的不就是……
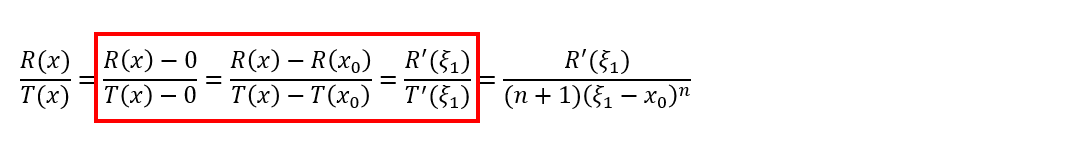
然后拉格朗日继续尝试,先看分子:
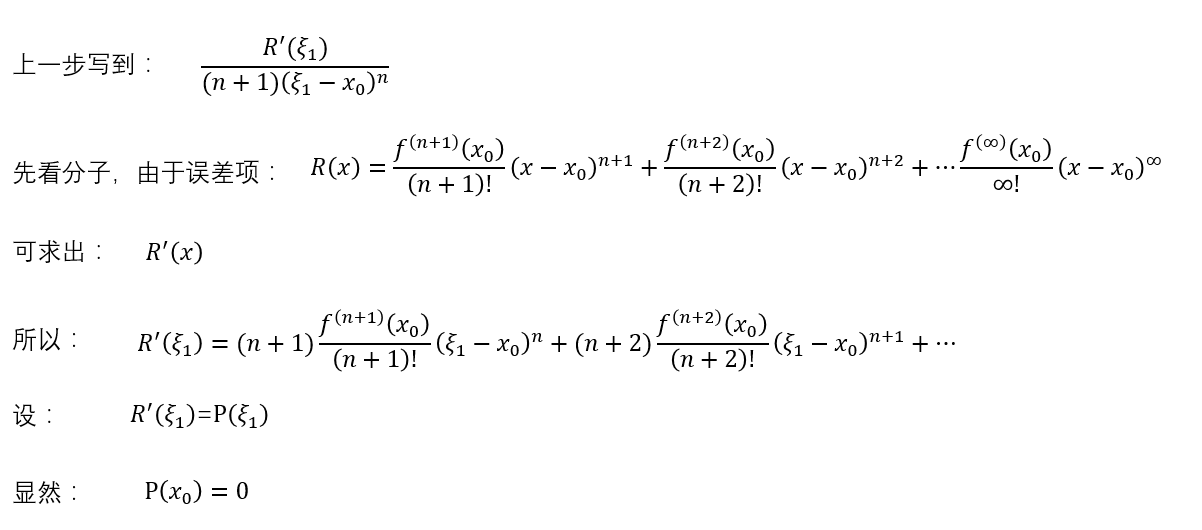
再看分母:
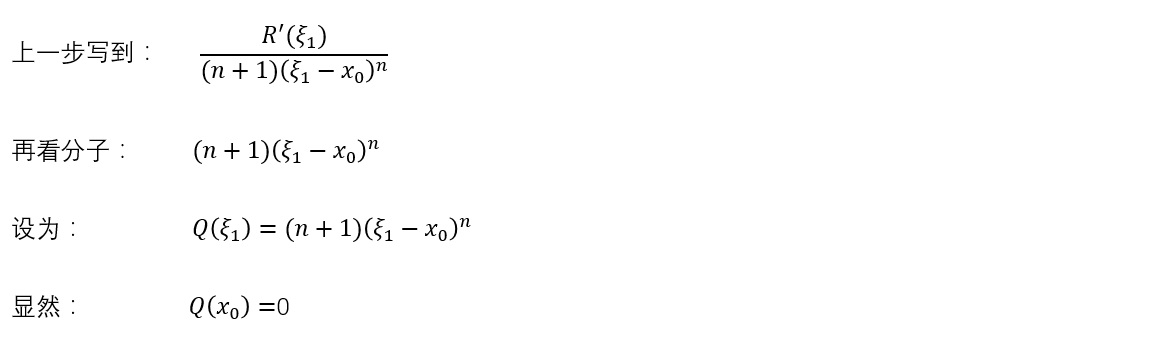
好巧,又可以用一次柯西的中值定理了。
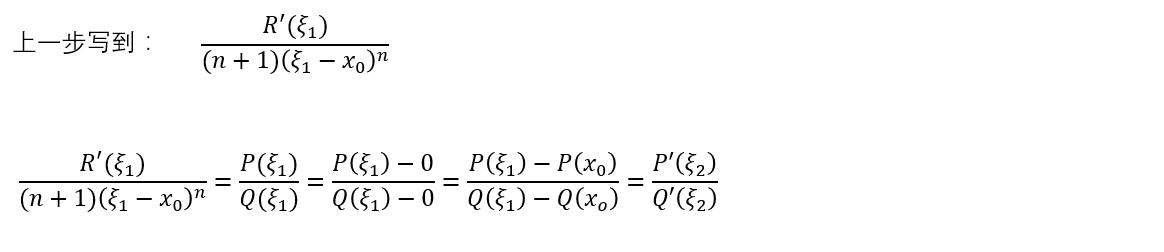
总之,按照这种方法,可以一直求解下去,最终的结果就是:误差项 = \({\frac {f^{n+1}(ξ)} {(n+1)!}}(x - x_{0})^{n+1}\)
至此,拉格朗日把后面无数多的误差项给整合成了一项,而且比配诺亚更加先进的地方在于,不一定非要让 \(x\) 趋近于 \(x_{0}\),可以在二者之间的任何一个位置 ξ 处展开,极其好用。
本文来自于:知乎陈二喜,一个骚气十足的美男子,拥有着万里挑一的有趣灵魂。
如果觉得文章对您有所帮助,可以请囊中羞涩的作者喝杯柠檬水,万分感谢,愿每一个来到这里的人都生活愉快,幸福美满。
微信赞赏

支付宝赞赏



