解密数据结构：堆，从零开始使用 Cython 带你实现一个 heapq 模块

楔子

Python 有一个内置的模块叫 heapq，从名字上看它和堆有关系，我们先来看看这个模块都有哪些功能吧。

import heapq

data = [4, 9, 1, 5, 6, 2, 7, 3, 8]
# 将 data 调整为一个堆，关于堆后面会详细介绍
# 总之堆有两种，分别是大根堆和小根堆，heapify(data) 得到的是小根堆
# 大根堆的第一个元素永远是最大值，小根堆的第一个元素永远是最小值
heapq.heapify(data)
print(data)  # [1, 3, 2, 5, 6, 4, 7, 9, 8]

# 从堆顶弹出一个元素，也就是最小值
# 然后维护剩余元素，形成新的堆
item = heapq.heappop(data)
print(item)  # 1
print(data)  # [2, 3, 4, 5, 6, 8, 7, 9]

# 往堆中添加一个元素，1 是最小值，显然它会进入堆顶
heapq.heappush(data, 1)
print(data)  # [1, 2, 4, 3, 6, 8, 7, 9, 5]

# 往堆中添加一个元素的同时，弹出堆顶元素
item = heapq.heapreplace(data, 10)
print(item)  # 1
print(data)  # [2, 3, 4, 5, 6, 8, 7, 9, 10]

# 从堆中选择 n 个最大的元素（从大到小排序）
print(heapq.nlargest(3, data))  # [10, 9, 8]

# 从堆中选择 n 个最小的元素（从小到大排序）
print(heapq.nsmallest(3, data))  # [2, 3, 4]

# 将多个有序数组合并成新的有序数组
print(
    list(heapq.merge([1,3,5,7], [0,2,4,8], [5,10,15,20], [], [25]))
)  # [0, 1, 2, 3, 4, 5, 5, 7, 8, 10, 15, 20, 25]

可以看到这个模块的功能还是很强大的，当然我们的重点不只是介绍这个模块的用法，因为用法太简单了，我们主要是想介绍背后的数据结构：堆。注意，堆是一种非常高效的数据结构，我们可以用它实现优先队列，堆实现的优先队列在元素入队、出队的时间复杂度上均为 \(O(logN)\)。

那么下面我们就来介绍一下堆这种数据结构，并且后续用 Cython 手动实现一个 heapq，然后和标准库 heapq 进行一下对比，看看哪个效率更高。

因为 heapq 底层是用 C 实现的，所以我们也要用 Cython 去写，然后进行 PK 才比较公平。

什么是堆？

首先堆本身就是一颗树，如果这颗树是一颗二叉树，那么实现的堆的就被称为二叉堆。当然除了二叉堆，还有三叉堆等等，只不过二叉堆是一种最主流的堆的实现方式。因此，堆（二叉堆）就是一颗满足一些特殊性质的二叉树，那么问题来了，它都满足哪些性质呢？

首先它是一个完全二叉树；其次，每个节点都比它的左右孩子节点大（或者小）。如果每个节点都比孩子节点大，那么这个堆就是大根堆，每个节点都比孩子节点小，那么这个堆就是小根堆。

注意：堆要求的是每个节点和其父节点之间满足相应的大小关系，如果两个节点之间没有父子关系，那么它们谁大谁小无关紧要。比如第三层的最后一个节点是 13，但是第四层的节点却都比它大，但它们之间没有父子关系，所以我们当前这个堆是成立的。只要每个节点都比它的父节点大（小）即可，或者说只要每个节点都比它的孩子节点大（小）即可。

正因为堆的这个性质，我们可以使用数组来表示堆，直接按照层序遍历的方式将每一层的元素放在数组中即可，比如：

[62, 41, 30, 28, 16, 22, 13, 19, 17, 15]

很明显，堆顶（数组索引为 0）的元素永远是值最大或最小的元素，取决于你构建的是大根堆还是小根堆。

但是问题来了，如果我有一个节点，我要如何找到它的父节点或者孩子节点呢？结论如下，假设当前节点所在的索引为 n：

• 父节点的索引：(n - 1) / 2
• 左孩子节点的索引：2n + 1
• 右孩子节点的索引：2n + 2

我们以索引为 3 这个元素（值为 28）为例，它父节点的索引就是 (3 - 1) / 2 = 1，也就是 41 这个元素；左孩子节点的索引就是 2 * 3 + 1 = 7，也就是 19 这个元素；右孩子节点的索引显然是 8，也就是 17 这个元素。可以对照上图，检验一下是否有误，或者你也可以创建一个更大的堆，自己测试一下，但前提必须是完全二叉树才具备这个性质。

补充一些二叉堆的性质：显然二叉堆每一层的所能容纳的最大元素个数构成一个公比为 2 的等比数列，第 K 层的元素个数就是 2 ** (K - 1)，K 从 1 开始。比如第一层最多容纳 1 个元素、第二层最多容纳 2 个元素、第三层最多容纳 4 个元素。

并且第 K 层能容纳的最大元素个数等于前 K - 1 层的元素个数之和再加 1，比如第 4 层最多容纳 8 个元素，第 1 层、第 2 层、第 3 层分别能容纳 1、2、4 个元素，而 8 = (1 + 2 + 4) + 1。

由此我们可以得到第三个结论，如果堆有 N 层，那么堆上的元素至少有 2 ** (N -1) 个，此时第 N 层只有 1 个元素，前 N - 1 层有 2 ** (N -1) - 1 个元素（第 N 能容纳的最大元素个数减去 1），加起来是 2 ** (N -1) 个；最多有 2 ** N - 1 个，第 N + 1 层所能容纳的最大元素个数减去 1。

最后，如果二叉堆有 M 个元素，那么层数为 log2(M) 向下取整再加 1。

显然通过这种方式，我们就不需要两个指针来维持节点之间的父子关系了，并且通过索引定位元素速度也会更快。接下来我们就来看看如何往堆中添加元素。

往堆中添加元素（Sift Up）

首先堆是一个完全二叉树，往堆中添加一个元素，从树的层面上来看，就是往最后一层的最右端添加一个元素，如果最后一层已经没有元素了，那么就新加一层。如果从数组的层面上来看，就相当于 append 一个元素。

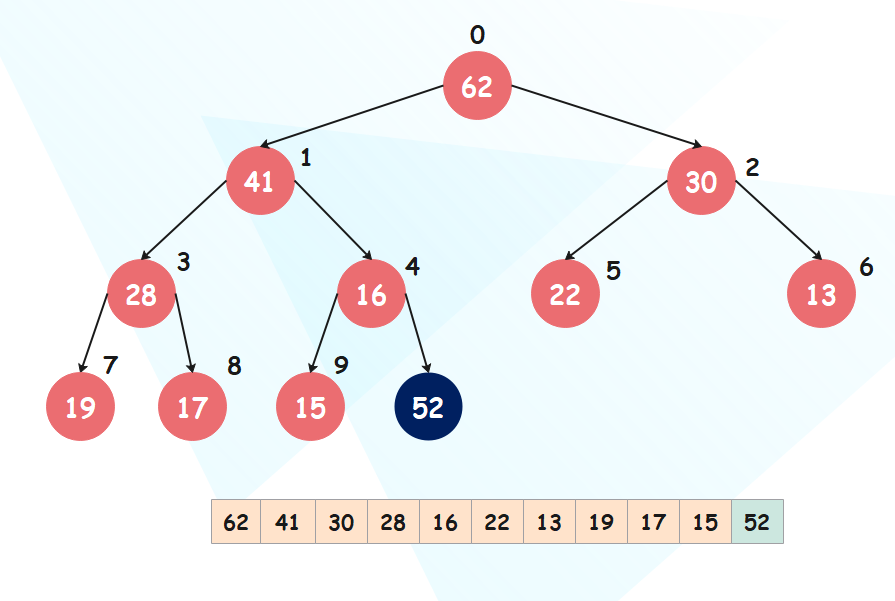
非常简单，不过还没有结束，因为堆有两个性质，虽然我们添加元素之后仍然满足是一颗完全二叉树，但是不满足子节点都不大于它的父节点（这里我们构建的是大根堆）。所以我们还要进行调整，将新添加的元素放到属于它的位置，具体过程也很简单：将该元素和它的父节点进行比较，如果比它的父节点大，那么就进行交换，交换之后再和它新的父节点进行比较，如果还大于新的父节点则继续交换，直到不大于为止。所以从尾部添加的节点，一直向上浮动，直到找到属于它的位置，因此这个过程也被成为 Sift Up（上浮）。

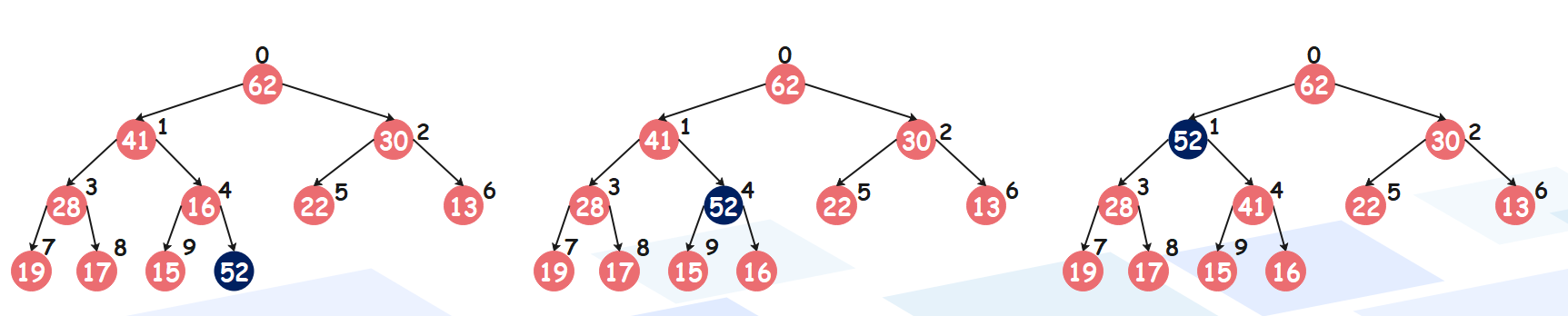
当交换之后，发现不大于它的父节点，那么该元素就可以停下来了。可能有人问，它父节点的父节点、爷爷节点该怎么办？答案是不需要关心，因为大根堆的性质就是子节点不大于父节点，所以当新添加的元素不大于它的父节点时，也更不可能大于父节点的父节点、爷爷节点。

下面我们就编写代码实现一下：

cdef class BinaryHeap:

    # 通过数组来模拟堆，为避免直接修改对，这个堆不对外暴露
    # 而是专门提供一个接口
    cdef list data

    def __init__(self):
        self.data = []

    cdef inline Py_ssize_t get_parent(self, Py_ssize_t n):
        # 根据节点的索引找到其父节点的索引
        return (n - 1) // 2

    cdef inline Py_ssize_t get_left_child(self, Py_ssize_t n):
        # 根据节点的索引找到其左孩子节点的索引
        return 2 * n + 1

    cdef inline Py_ssize_t get_right_child(self, Py_ssize_t n):
        # 根据节点的索引找到其右孩子节点的索引
        return 2 * n + 2

    cpdef heappush(self, item):
        # 往堆中添加一个元素，我们说对于数组而言，直接 append 即可
        # 注意这里的 item 我们没有限制它的类型，可以是数值、字符串、元组，只要彼此能比较就行
        self.data.append(item)
        # 但是还没有结束，添加完之后我们还要对堆进行调整，由 sift_up 函数负责，它接收一个索引
        # 显然我们是对最后一个元素进行上浮，也就是索引为 len(self.data) - 1 位置的元素
        self.sift_up(len(self.data) - 1)

    cdef void sift_up(self, Py_ssize_t n):
        # 对指定索引位置的元素进行上浮
        cdef Py_ssize_t parent
        while n > 0:
            parent = self.get_parent(n)
            # 当该元素不是根节点的时候，将其和父节点进行比较
            # 如果大于父节点，两者进行交换
            if self.data[n] > self.data[parent]:
                self.data[n], self.data[parent] = self.data[parent], self.data[n]
                # 交换之后该节点成为了父节点，然后将 parent 赋值为 n
                # 因为它还要继续作为新的子节点和新的父节点比较
                n = parent
            else:
                # 如果不大于父节点，说明该元素已经找到属于它的位置了，直接将循环结束掉即可
                break

    cpdef str show_heap_info(self):
        # 专门提供一个接口，显示堆的信息
        if len(self.data) == 0:
            return ""
        import math
        cdef:
            Py_ssize_t depths = int(math.log2(len(self.data))) + 1
            Py_ssize_t i
            list pretty_info = []
        for depth in range(0, depths):
            s = "  ".join(map(str, self.data[2 ** depth - 1: 2 ** (depth + 1) - 1]))
            pretty_info.append(f"第 {depth + 1} 层：{s}")
        return "\n".join(pretty_info)

以上代码所在文件为 my_heap.pyx，我们编译之后导入测试：

import my_heapq
heap = my_heapq.BinaryHeap()

for item in [62, 41, 30, 28, 16, 22, 13, 19, 17, 15]:
    heap.heappush(item)
print(heap.show_heap_info())
"""
第 1 层：62
第 2 层：41  30
第 3 层：28  16  22  13
第 4 层：19  17  15
"""
# 这个时候再添加一个元素 52
heap.heappush(52)
print(heap.show_heap_info())
"""
第 1 层：62
第 2 层：52  30
第 3 层：28  41  22  13
第 4 层：19  17  15  16
"""

可以看到结果是没有问题的，以上我们添加元素就成功了，下面我们再来看看如何从堆中取出元素。

从堆中取出元素（Sift Down）

正如添加元素从堆底添加，取出元素也只能从堆顶取出，不能取其它位置的元素。

但问题是，如果将堆顶的元素取走之后，那么就会形成两个独立的堆，堆的根节点分别是它的左右节点。所以我们还要手动将两个堆合并在一起，会比较麻烦，于是我们可以将堆顶和堆底的元素进行交换。交换之后，弹出堆底的元素，此时就得到了最大值。但此时不满足堆的第二个性质，所以我们还要进行调整，将根节点和左右子节点中大的那一个进行比较，如果比子节点小，那么进行交换，然后成为新的子节点。不断重复此过程，直到找到属于该元素的位置，这个过程也叫作 Sift Down。

下面我们来继续完善之前的 my_heap.pyx：

cdef class BinaryHeap:

    cdef list data

    def __init__(self):
        self.data = []

    cdef inline Py_ssize_t get_parent(self, Py_ssize_t n):
        return (n - 1) // 2

    cdef inline Py_ssize_t get_left_child(self, Py_ssize_t n):
        return 2 * n + 1

    cdef inline Py_ssize_t get_right_child(self, Py_ssize_t n):
        return 2 * n + 2

    cpdef heappush(self, item):
        self.data.append(item)
        self.sift_up(len(self.data) - 1)

    cdef void sift_up(self, Py_ssize_t n):
        # 上浮这一过程可以继续简化一下
        while n > 0 and self.data[n] > self.data[self.get_parent(n)]:
            self.data[n], self.data[self.get_parent(n)] = self.data[self.get_parent(n)], self.data[n]
            n = self.get_parent(n)

    cpdef heappop(self):
        if len(self.data) == 0:
            raise ValueError("heap is empty")
        # 只需要将第一个元素和最后一个元素进行交换，然后返回即可
        self.data[0], self.data[-1] = self.data[-1], self.data[0]
        # 不过在返回之前，记得调整一下堆
        self.sift_down(self, 0)
        return self.data.pop()

    cdef void sift_down(self, Py_ssize_t n):
        cdef Py_ssize_t left_child, right_child, child
        # 对索引为 n 的元素进行下沉，这里需要判断左孩子节点
        # 如果左孩子节点的索引越界，说明该节点已经是叶子节点了
        while self.get_left_child(n) < len(self.data):
            left_child = self.get_left_child(n)
            right_child = self.get_right_child(n)
            # 获取子节点大的那一个，注意：需要考虑右节点是否存在的情况
            child = (right_child
                     if right_child < len(self.data) and self.data[left_child] < self.data[right_child]
                     else left_child)
            # 将该节点和孩子节点进行比较，如果比孩子节点小，那么交换位置
            if self.data[n] < self.data[child]:
                n = child
            # 否则直接跳出循环
            else:
                break

    cpdef str show_heap_info(self):
        if len(self.data) == 0:
            return ""
        import math
        cdef:
            Py_ssize_t depths = int(math.log2(len(self.data))) + 1
            Py_ssize_t i
            list pretty_info = []
        for depth in range(0, depths):
            s = "  ".join(map(str, self.data[2 ** depth - 1: 2 ** (depth + 1) - 1]))
            pretty_info.append(f"第 {depth + 1} 层：{s}")
        return "\n".join(pretty_info)

编译测试一下：

import random
import my_heapq

heap = my_heapq.BinaryHeap()
# 生成 100 万个随机数
for i in range(1000000):
    heap.heappush(random.randint(1, 10000))
# 将这 100 万个随机数依次弹出，显然下面得到的 data 数组是有序的，这里是降序排序
data = [heap.heappop() for _ in range(1000000)]
# 我们验证一下
for index in range(len(data) - 1):
    # 如果 data[index] < data[index + 1]，证明我们 heappop 逻辑有问题
    if data[index] < data[index + 1]:
        raise ValueError("data[index] must be greater than or equal to data[index + 1]")
else:
    print("success")
"""
success
"""

显然是没有问题的，因此我们这里就实现了一个堆排序，只不过这个堆排序还不太完美，不完美之处有两个地方：

• 1. 默认是从大到小排序的，应该提供一个参数供外界选择究竟是从大到小还是从小到大
• 2. 这里开辟了一个额外的数组，合适的做法应该是接收一个数组，然后原地排序

当然我们只是为了介绍 Sift Up、Sift Down 而顺便实现的堆排序，那么接下来我们就来重新实现一下堆排序，不过在介绍之前，我们还需要了解一下两个前置知识。

heapify 和 replace

replace 相当于从堆中取出一个元素的同时再放入一个元素，具体做法很简单，直接将新加入的元素和堆顶元素替换一下，再将替换之前的堆顶元素返回即可。

cdef class BinaryHeap:

    cdef list data

    def __init__(self):
        self.data = []

    cdef void sift_down(self, Py_ssize_t n):
        cdef Py_ssize_t left_child, right_child, child
        while self.get_left_child(n) < len(self.data):
            left_child = self.get_left_child(n)
            right_child = self.get_right_child(n)
            child = (right_child
                     if right_child < len(self.data) and self.data[left_child] < self.data[right_child]
                     else left_child)
            if self.data[n] < self.data[child]:
                self.data[n], self.data[child] = self.data[child], self.data[n]
                n = child
            else:
                break

    cpdef replace(self, item):
        if len(self.data) == 0:
            raise ValueError("heap is empty")
        res = self.data[0]
        # 将堆顶元素替换成新加入的元素
        self.data[0] = item
        # 由于此时不一定满足堆的性质，所以需要调整一下堆
        self.sift_down(0)
        return res

代码有删减，只保留了当前需要的部分，其它部分不变。然后编译测试一下：

import random
import my_heapq

heap = my_heapq.BinaryHeap()
for i in range(20):
    heap.heappush(random.randint(1, 100))
print(heap.show_heap_info())
"""
第 1 层：98
第 2 层：94  76
第 3 层：76  90  73  60
第 4 层：66  60  72  36  47  10  35  58
第 5 层：3  16  4  10  15
"""
print(heap.replace(50))  # 98
print(heap.show_heap_info())
"""
第 1 层：94
第 2 层：90  76
第 3 层：76  72  73  60
第 4 层：66  60  50  36  47  10  35  58
第 5 层：3  16  4  10  15
"""

可以根据输出验证一下，结果是正确的。

然后在看一下 heapify，它是将任意一个数组整理成堆的形状，因为堆可以使用数组来模拟。所以只要任意一个数组，都可以通过元素交换的形式整理成堆的形状。具体做法也很简单，我们只需要从最后一个非叶子节点开始，不断地进行 SiftDown 操作即可，这里就不画图了，可以自己理解一下。

下面我们来实现一下，注意：接下来我们就不通过类的形式了，直接定义函数即可。

cdef inline Py_ssize_t get_parent(Py_ssize_t n):
    return (n - 1) >> 1

cdef inline Py_ssize_t get_left_child(Py_ssize_t n):
    return 2 * n + 1

cdef inline Py_ssize_t get_right_child(Py_ssize_t n):
    return 2 * n + 2

cdef void sift_down(list data, Py_ssize_t n):
    # 对索引为 n 的元素进行下沉操作
    cdef Py_ssize_t left_child, right_child, child
    while get_left_child(n) < len(data):
        left_child = get_left_child(n)
        right_child = get_right_child(n)
        child = (right_child
                 if right_child < len(data) and data[left_child] < data[right_child]
                 else left_child)
        if data[n] < data[child]:
            data[n], data[child] = data[child], data[n]
            n = child
        else:
            break

def heapify(list data not None):
    # 从最后一个非叶子点进行 SiftDown
    for n in range((len(data) - 1) >> 1, -1, -1):
        sift_down(data, n)

重新编译，然后测试一下：

import random
import my_heapq

data = [random.randint(10, 100) for _ in range(15)]
print(data)  # [64, 60, 25, 70, 36, 40, 17, 61, 16, 25, 29, 20, 60, 10, 52]
my_heapq.heapify(data)
print(data)  # [70, 64, 60, 61, 36, 40, 52, 60, 16, 25, 29, 20, 25, 10, 17]
"""
                                       70
                       64                              60
                61            36                 40           52
            60      16    25     29           20     25   10      17 
"""

显然是满足堆的性质的，并且这个操作是一个时间复杂度为 O(N)、空间复杂度为 O(1) 的操作。

然后我们就可以实现我们的堆排序了。

cdef inline Py_ssize_t get_parent(Py_ssize_t n):
    return (n - 1) >> 1

cdef inline Py_ssize_t get_left_child(Py_ssize_t n):
    return 2 * n + 1

cdef inline Py_ssize_t get_right_child(Py_ssize_t n):
    return 2 * n + 2

cdef void sift_down(list data, Py_ssize_t n, Py_ssize_t length):
    # 对索引为 n 的元素进行下沉操作，但这里多了一个 length，为什么呢？
    # 首先我们之前是将堆顶和堆底的元素交换之后，就将堆底的元素弹出去了
    # 以至于我们需要单独开辟一个数组去接收
    # 但很明显，我们这里要求原地排序，那么交换之后的元素在堆底不可以动
    # 因此每 sift_down 一次，length 要减去 1
    cdef Py_ssize_t left_child, right_child, child
    while get_left_child(n) < length:
        left_child = get_left_child(n)
        right_child = get_right_child(n)
        child = (right_child
                 if right_child < length and data[left_child] < data[right_child]
                 else left_child)
        if data[n] < data[child]:
            data[n], data[child] = data[child], data[n]
            n = child
        else:
            break

def heapify(list data not None):
    # 从最后一个非叶子点进行 SiftDown
    for n in range((len(data) - 1) >> 1, -1, -1):
        sift_down(data, n, len(data))

def heap_sort(list data not None, bint reverse=False):
    # 首先将其整理成堆的形状
    heapify(data)
    # 然后挨个出数
    cdef Py_ssize_t i
    for i in range(len(data) - 1, -1, -1):
        # 交换完之后的元素就不可以动了
        data[0], data[i] = data[i], data[0]
        # 并且也不能再参与后续的 sift_down
        # 因此依旧调整堆，但是范围变了，比如第一次交换，那么最后一个元素为最大值
        # 再次 sift_down 的时候，整个范围就是 0 到 len(data) - 1
        # 同理第二次 sift_down 的时候，范围就是 0 到 len(data) - 2
        sift_down(data, 0, i)

    # 如果逆序排序，那么首尾元素依次交换
    if reverse:
        length = len(data)
        for i in range(length >> 1):
            data[i], data[length - 1 - i] = data[length - 1 - i], data[i]

测试一下：

import random
import my_heapq

data = [random.randint(10, 100) for _ in range(15)]
print(data)  # [80, 41, 89, 70, 99, 10, 36, 58, 19, 82, 13, 25, 79, 59, 80]
my_heapq.heap_sort(data)
print(data)  # [10, 13, 19, 25, 36, 41, 58, 59, 70, 79, 80, 80, 82, 89, 99]

data = [random.randint(10, 100) for _ in range(15)]
print(data)  # [85, 24, 48, 71, 43, 82, 90, 99, 36, 25, 46, 25, 63, 47, 12]
my_heapq.heap_sort(data, reverse=True)
print(data)  # [99, 90, 85, 82, 71, 63, 48, 47, 46, 43, 36, 25, 25, 24, 12]

怎么样，是不是很简单呢？但是在排序的时候，堆排序不是效率最高的排序，它比归并、三路快排要慢一些。因为堆存在的目的绝不仅仅是为了排序，由于其可以动态添加元素、删除元素，并且时间复杂度都为 O(logN) 级别，所以它的强大之处就在于其非常适合实现优先队列，堆是一种非常不错的选择。Python 的优先队列，底层就是借助于堆实现的，我们看一下：

里面的 item 是一个元组，第一个元素非优先级（值越大、优先级越高），第二个元素是 data，这就是优先队列，是不是比你想象中的要简单许多呢？

Top k 问题

我们经常会遇到从数组中选择 k 个最大或最小的元素，最简单的做法就是对数组排个序，然后截取前 k 个元素即可。但这样做会产生性能上的浪费，因为我们需要先对数组进行全局排序，但这其实是没有必要的。最好的做法是将数组变成一个堆，然后选择前 k 个最大或最小的元素，我们不妨测试一下两者的性能差异：

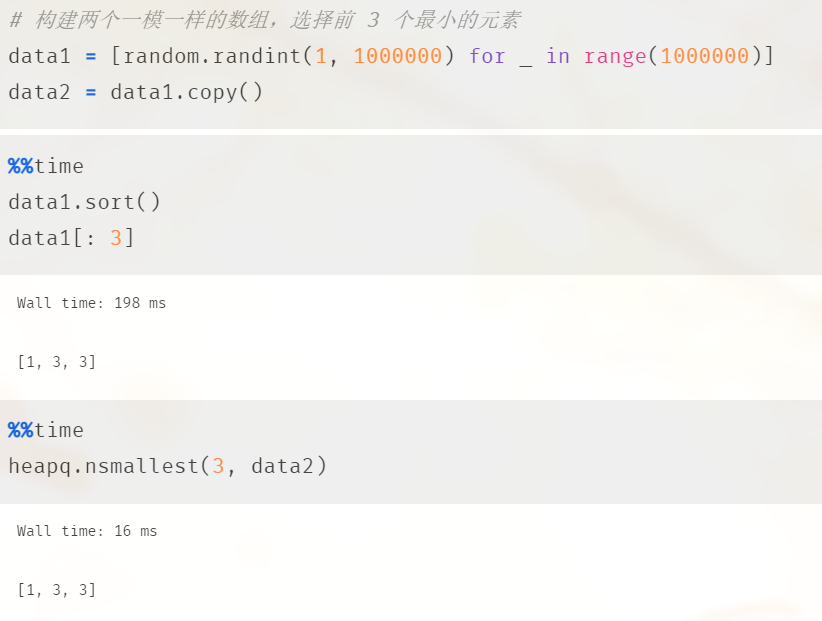
我们看到性能差了有 10 倍，所以使用堆的方式要更加快速，那么该如何实现呢？假设我们要选取 k 个最小的元素，那么首先我们可以从数组中截取前 k 个元素，构建一个大根堆。然后从第 k + 1 个元素开始遍历数组，如果遍历的元素大于等于堆顶元素，那么它肯定就不是前 k 小的元素，如果遍历的元素小于堆顶的元素，那么两者进行交换，然后进行一次 Sift Down 操作。当数组遍历完毕之后，堆中的 k 个元素就是最小的元素。同理，如果想选择前 k 个最大的元素，那么就构建一个小根堆。

或者将整个数组构建成一个堆，然后排序 k 次即可，这样也能选择前 k 个元素。

这里我们先不实现，我们下面来手动实现 heapq 模块，然后在里面实现所有功能。

手动实现 heapq 模块

heapq 的功能，我们在最开始的时候就已经见过了，我们针对里面的功能重新实现一遍，然后对比一下两者的性能差异。这里我们就从头开始一点一点实现，每一步也都会有相应的注释。

cdef inline Py_ssize_t get_parent(Py_ssize_t n):
    """
    根据节点的索引返回其父节点的索引
    :param n: 索引 
    :return: 
    """
    return (n - 1) >> 1

cdef inline Py_ssize_t get_left_child(Py_ssize_t n):
    """
    根据节点的索引返回其左孩子节点的索引
    :param n: 索引
    :return: 
    """
    return 2 * n + 1

cdef inline Py_ssize_t get_right_child(Py_ssize_t n):
    """
    根据节点的索引返回其右孩子节点的索引
    :param n: 索引
    :return: 
    """
    return 2 * n + 2

cdef sift_up_large(list data, Py_ssize_t n):
    """
    将索引为 n 的元素进行上浮，用于构建大根堆
    :param data: 数组 
    :param n: 索引
    :return: 
    """
    # 当该元素比它的父节点大，那么交换两者的位置，因为大根堆要求父节点不能小于孩子节点
    # 而一旦找到比它大的父节点，该元素的位置就已经确定了，循环就会结束
    while n > 0 and data[n] > data[get_parent(n)]:
        data[n], data[get_parent(n)] = data[get_parent(n)], data[n]
        # 交换之后成为父节点之后还没有结束，还和作为新的字节点和新的父节点继续比较
        n = get_parent(n)

cdef sift_up_small(list data, Py_ssize_t n):
    """
    将索引为 n 的元素进行上浮，用于构建小根堆
    :param data: 数组 
    :param n: 索引
    :return: 
    """
    # 当该元素比它的父节点小，那么交换两者的位置，因为小根堆要求父节点不能大于孩子节点
    # 而一旦找到比它小的父节点，该元素的位置就已经确定了，循环就会结束
    while n > 0 and data[n] < data[get_parent(n)]:
        data[n], data[get_parent(n)] = data[get_parent(n)], data[n]
        # 交换之后成为父节点之后还没有结束，还和作为新的字节点和新的父节点继续比较
        n = get_parent(n)

cdef sift_down_large(list data, Py_ssize_t n, Py_ssize_t length):
    """
    将索引为 n 的元素进行下沉，用于构建大根堆
    :param data: 数组
    :param n: 索引
    :param length: 可以看到的数组长度 
    :return: 
    """
    cdef Py_ssize_t left_child, right_child, child
    # 如果左孩子所在索引不小于 length，说明该节点是叶子节点，也就无需下沉了
    while get_left_child(n) < length:
        left_child = get_left_child(n)
        right_child = get_right_child(n)
        # 判断是否有右孩子，如果有右孩子，那么选择值较大的那一个孩子节点
        child = (right_child
                 if right_child < length and data[left_child] < data[right_child]
                 else left_child)
        # 如果该元素比孩子节点的值小，那么两者进行交换，因为大根堆要求父节点不小于子节点
        if data[n] < data[child]:
            data[n], data[child] = data[child], data[n]
            # 该元素成为子节点之后还要继续比较，还要作为新的父节点和新的子节点继续比较
            n = child
        # 否则下沉操作就可以结束了，直接 break
        else:
            break

cdef sift_down_small(list data, Py_ssize_t n, Py_ssize_t length):
    """
    将索引为 n 的元素进行下沉，用于构建小根堆
    :param data: 数组
    :param n: 索引
    :param length: 可以看到的数组长度 
    :return: 
    """
    cdef Py_ssize_t left_child, right_child, child
    # 如果左孩子所在索引不小于 length，说明该节点是叶子节点，也就无需下沉了
    while get_left_child(n) < length:
        left_child = get_left_child(n)
        right_child = get_right_child(n)
        # 判断是否有右孩子，如果有右孩子，那么选择值较小的那一个孩子节点
        child = (right_child
                 if right_child < length and data[left_child] > data[right_child]
                 else left_child)
        # 如果该元素比孩子节点的值大，那么两者进行交换，因为小根堆要求父节点不大于子节点
        if data[n] > data[child]:
            data[n], data[child] = data[child], data[n]
            # 该元素成为子节点之后还要继续比较，还要作为新的父节点和新的子节点继续比较
            n = child
        # 否则下沉操作就可以结束了，直接 break
        else:
            break

# 以上就完成最大堆、最小堆的上浮和下沉操作

def heappush(list data not None, item):
    """
    往堆中添加一个元素
    注意：这里的 data 是由外界传递的，所以外界需要确保传递的 data 满足堆的形状
    :param data: 数组
    :param item: 要添加的元素
    :return:
    """
    # 将元素追加到尾部
    data.append(item)
    # 对最后一个元素进行上浮操作，因为是小根堆，所以采用 sift_up_small
    sift_up_small(data, len(data) - 1)

def heappop(list data not None):
    """
    弹出堆顶的元素，因为是小根堆，所以弹出的是最小值
    注意：data 同样需要满足堆的形状
    :param data: 数组
    :return:
    """
    if len(data) == 0:
        raise ValueError("heap is empty")
    # 将堆顶和堆底的元素进行交换
    data[0], data[-1] = data[-1], data[0]
    # 此时需要重新调整堆，对堆顶的元素执行下沉操作
    # 因为最后一个元素是即将要被弹出的最小值，所以它不可以参与下沉操作
    # 因此 length 是 len(data) - 1
    sift_down_small(data, 0, len(data) - 1)
    return data.pop()

def heapreplace(list data not None, item):
    """
    弹出堆顶元素的同时，再添加一个元素
    注意：data 同样需要满足堆的形状
    :param data: 数组
    :param item: 要添加的元素
    :return:
    """
    if len(data) == 0:
        raise ValueError("heap is empty")
    # 将堆顶的元素先保存起来，然后再将堆顶元素替换成指定的 item
    # 所以直接交换 item 和 data[0] 即可
    item, data[0] = data[0], item
    # 重新调整堆，对堆顶的元素执行下沉操作，针对小根堆
    # 因为 heapify 调整之后的结果就是小根堆
    sift_down_small(data, 0, len(data))
    # 返回 item，也就是之前堆顶的元素，显然也是之前堆中的最小元素
    return item

def heappushpop(list data not None, item):
    """
    先添加一个元素，再弹出一个元素，所以它和 heapreplace 的区别就是
        + heapreplace 是先弹出元素、再添加元素
        + heappushpop 是先添加元素、再弹出元素
    因此 heappushpop 允许堆为空
    注意：data 同样需要满足堆的形状
    :param data: 数组
    :param item: 要添加的元素
    :return:
    """
    # 如果堆为空，或者堆顶的元素不小于 item，那么 item 添加进堆之后一定就是最小值，位于堆顶
    # 所以此时也就没有必要添加了，因为加入之后再弹出去的还是它本身，整个堆没有变化
    # 但需要额外做一次堆调整操作，因此当下面的 if 条件不成立时，直接返回 item 即可
    if data and data[0] < item:
        # 否则相当于 heapreplace
        item, data[0] = data[0], item
        sift_down_small(data, 0, len(data))
    return item

def heapify(list data not None):
    """
    将任意一个数组变成一个堆，这里我们采用小根堆， 因为 heapq 里面的的 heapify 就是小根堆
    当然我们可以做的更智能一点，采用参数控制，但是 heappop 出来的值会有所变化
    如果是小根堆，heappop 出来的是最小值，如果是大根堆，heappop 出来的就是最大值
    :param data: 数组
    :return:
    """
    for n in range((len(data) - 1) >> 1, -1, -1):
        sift_down_small(data, n, len(data))

cdef heapify_large(list data):
    """
    这里我们额外实现一个大根堆，但是不对外暴露
    :param data: 数组
    :return: 
    """
    for n in range((len(data) - 1) >> 1, -1, -1):
        sift_down_large(data, n, len(data))

def nsmallest(Py_ssize_t n, data not None, key=None):
    """
    选择前 n 个最小的元素，我们说过有两种做法
    第一种:
        选择数组的前 n 个元素构建一个大根堆，然后从数组的第 n + 1 个元素开始遍历
        如果元素大于等于堆顶元素，说明它一定不是前 n 个最小的元素，因为此时已经有 n 个元素小于等于它了
        如果小于堆顶元素，那么和堆顶元素进行替换，然后重新调整堆，让堆顶继续成为最大的元素
        然后一直重复此过程，当遍历结束时，这个堆维护的 n 个元素就是最小的元素
    第二种：
        将整个数组构建成一个小根堆，然后使用堆排序，但是只排序 n 次
        然后数组的最后 n 个元素就是整个数组前 n 个最小的元素
    由于堆排序我们实现过了，所以这里采取第一种做法
    :param n: 选择最小的元素的个数
    :param data: 这里我们不要求 data 满足堆的形状，所以它可以不是列表
    :param key: 比较函数，个人觉得这是 Python 的一个非常强大的功能
    :return:
    """
    # 快分支，如果 n == 1 的话，那么直接使用内置函数 min
    if n == 1:
        # 如果 data 为空，那么使用 min 会报错，于是可以通过 default 参数设置一个哨兵
        # 当 data 为空的时候返回 default 指定的值
        res = min(data, default=None, key=key)
        # 如果 res 为 None，那么返回空列表，否则返回 [res]
        return [] if res is None else [res]
    # 然后判断 n 是否大于等于 data 的总长度，如果大于的话直接将整个数组排序之后返回
    # 这里需要检测 data 是否有 __len__ 方法，否则它没法调用内置函数 len
    # 像我们自定义的实现了 __iter__、__next__ 的类的实例对象，它们虽然没有 __len__，但是可以排序
    # 不过这种情况有点少见，Python 内置的容器对象都有 __len__
    # 主要 heapq 里面考虑了这种情况，所以我们也考虑
    if hasattr(data, "__len__") and len(data) <= n:
        return sorted(data, key=key)

    # 存放前 n 个元素的数组
    cdef list result

    if key is None:
        # 选择前 n 个元素，用于构建大根堆
        # 因为我们不知道 data 能否通过索引或者切片的方式去获取，所以采用迭代器的方式
        data_it = iter(data)
        # 截取前 n 个元素，这里通过 zip 的方式，这样即使长度小于 n 也不会报错
        result = [item for i, item in zip(range(n), data_it)]
        # 如果 result 为空，直接返回
        if not result:
            return result
        # 将 result 调整成大根堆
        heapify_large(result)
        # 遍历剩下的元素
        for item in data_it:
            # 如果 result[0] <= item，那么 item 一定不可能是前 n 小的元素
            # 否则用 item 替换掉堆顶元素，显然这个过程类似 heapreplace，只不过返回值我们不需要
            # 但是注意：我们还不能直接用 heapreplace，因为它在替换元素之后维护的是最小堆
            if result[0] > item:
                # 将 item 替换掉堆顶元素，然后维护大根堆
                result[0] = item
                sift_down_large(result, 0, len(result))
        # 遍历完之后，result 就维护了 n 个最小的元素
        # 将 result 排个序，然后返回
        result.sort()
        return result

    # 以上是 key 为 None 的情况，如果 key 不为 None，那么需要按照 key 的规则进行排序
    # 比如传递的 data 里面存放的是字典，默认字典之间是无法比较大小的
    # 但我们可以自定义比较逻辑，比如按照字典的某个 key 对应的 value 进行比较等等
    data_it = iter(data)
    # 截取前 n 个元素，并构建成一个元组，之后排序的时候就会按照 key(item) 进行排序
    # 最后只要返回 result 里面每个元组中的最后一个元素即可
    # 可能有人好奇元组里面的 i 是不是有点多余，答案是不多余
    # 在不指定 key 的时候 item 必须是可比较的，没什么好说的
    # 但当指定了 key，就意味着 item 可以是不可比较的
    # 那么当 key(item) 相同时，如果没有 i 就会比较 item，所以此时会报错
    # 当元组中多了一个 i 时，由于 i 是递增的值，因此一定可以比较出结果，也就是会按照先后顺序排序
    result = [(key(item), i, item) for i, item in zip(range(n), data_it)]
    # result 为空直接返回
    if not result:
        return result
    # 调整为大根堆
    heapify_large(result)
    for item in data_it:
        k = key(item)
        if result[0][0] > k:
            result[0] = (k, n, item)
            sift_down_large(result, 0, len(result))
            # 别忘记将 n 自增
            n += 1
    # 将 result 再排个序，key(item) 相同，则按照出现的先后顺序排序
    result.sort()
    return [item for *_, item in result]

def nlargest(Py_ssize_t n, data not None, key=None):
    """
    选择数组的前 n 个元素构建一个小根堆，然后从数组的第 n + 1 个元素开始遍历
    如果元素小于等于堆顶元素，说明它一定不是前 n 个最大的元素，因为此时已经有 n 个元素大于等于它了
    如果大于堆顶元素，那么和堆顶元素进行替换，然后重新调整堆，让堆顶继续成为最小的元素
    然后一直重复此过程，当遍历结束时，这个堆维护的 n 个元素就是最大的元素
    :param n: 选择最小的元素的个数
    :param data: 这里我们不要求 data 满足堆的形状，所以它可以不是列表
    :param key: 比较函数
    :return:
    """
    # 快分支，如果 n == 1 的话，那么直接使用内置函数 max
    if n == 1:
        res = max(data, default=None, key=key)
        return [] if res is None else [res]
    if hasattr(data, "__len__") and len(data) <= n:
        return sorted(data, key=key, reverse=True)

    # 存放前 n 个元素的数组
    cdef list result

    if key is None:
        # 选择前 n 个元素，用于构建小根堆
        data_it = iter(data)
        result = [item for i, item in zip(range(n), data_it)]
        # 如果 result 为空，直接返回
        if not result:
            return result
        # 将 result 调整成小根堆
        heapify(result)
        # 遍历剩下的元素
        for item in data_it:
            if result[0] < item:
                # 将 item 替换掉堆顶元素，然后维护小根堆
                result[0] = item
                sift_down_small(result, 0, len(result))
        result.sort(reverse=True)
        return result

    data_it = iter(data)
    result = [(key(item), i, item) for i, item in zip(range(n), data_it)]
    # result 为空直接返回
    if not result:
        return result
    # 调整为小根堆
    heapify(result)
    for item in data_it:
        k = key(item)
        if result[0][0] < k:
            result[0] = (k, n, item)
            sift_down_small(result, 0, len(result))
            # 别忘记将 n 自增
            n += 1
    result.sort(reverse=True)
    return [item for *_, item in result]

def merge(*iterables, key=None):
    """
    接收任意个有序数组，合并成一个新的有序数组
    最简单的做法是通过 sorted(itertools.chain(*iterables))
    虽然该做法是可以的，但显然时间复杂度较高，因为合并的是有序数组
    所以我们还是使用堆来实现
    :param iterables:
    :param key:
    :return:
    """
    cdef list result = []
    if key is None:
        for order, it in enumerate(map(iter, iterables)):
            # map(iter, iterables) 是将传递的每一个数组（也不一定是数组）都变成一个迭代器
            # 再套上 enumerate，遍历的时候可以同时下标
            try:
                _next = it.__next__  # 获取内部的 __next__ 方法
                # 整个循环结束之后，result 里面会有 len(iterables) 个列表
                # 每个列表中有三个元素，第一个元素就是对应的 iterable 的首元素
                # 第二个元素是 order，也就是下标，第三个元素是对应的 __next__ 方法
                result.append([_next(), order, _next])
            # 这里要进行异常捕获，因为可能传递了一个空数组
            except StopIteration:
                pass
        # 调整为小根堆，会先按照每个数组中的首元素进行排序
        # 如果首元素相同，那么按照 order、也就是先后顺序排序
        heapify(result)
        # 当 result 的长度大于 1 时，至于原因后面有解释
        while len(result) > 1:
            try:
                while True:
                    # 获取 result 中的首元素，因为每个数组都是有序的
                    # 所以它们的首元素调整为小根堆之后，显然 value 就是最小值
                    value, order, _next = s = result[0]
                    # 直接 yield 出去
                    yield value
                    # _next 保存对应数组的 __next__ 方法，所以我们要将它的下一个元素弹出来
                    # 替换掉堆顶的元素，当然了堆顶的元素是一个数组
                    s[0] = _next()
                    result[0] = s
                    # 调整成小根堆
                    sift_down_small(result, 0, len(result))
            # 有可能该数组已经没有元素可以迭代了，会抛出异常，那么我们就直接将首元素其从堆顶弹出
            except StopIteration:
                heappop(result)
        # 这里解释一下上面的 while len(result) > 1，假设我们传递了 3 个数组，分别是 arr0、arr1、arr2
        # 初始的 result 存放的元素就是：
        # [ [arr0[0], 0, arr0.__next__], [arr1[0], 1, arr1.__next__], [arr2[0], 0, arr2.__next__] ]
        # 假设初始的时候 arr1[0] 最小，那么弹出去之后，就会往堆中放入 [arr1[1], 1, arr1.__next__]
        # 因为数组的第三个元素保存了该数组的 __next__ 方法，假设之后 arr2[0] 最小，那么弹出之后
        # 再放入 [arr2[1], 1, arr1.__next__]，就这样重复此过程，直到每个数组（对应的迭代器）的元素消耗殆尽
        # 最终只会保留一个数组
        if result:
            # 获取 result 中最后一个数组
            value, order, _next = result[0]
            # 将 value 返回
            yield value
            # 但是还没有结束，因为对应的数组内部可能还有元素
            # 直接使用 yield from 将剩余的元素再依次迭代出去
            yield from _next.__self__
        return

    # 如果 key 不为 None
    for order, it in enumerate(map(iter, iterables)):
        try:
            _next = it.__next__
            value = _next()
            # 做法类似 nsmallest，只需要在开头加上 key(value) 即可
            # 这样就会按照自定义的逻辑进行排序
            # 但需要注意的是，我们的 value 和 order 交换了顺序
            # 这是因为指定了 key，那么 value 不要求必须是可比较的，因为我们指定了比较逻辑
            # 所以 key(value) 如果相同，那么应该按照 order 排序
            result.append([key(value), order, value, _next])
        except StopIteration:
            pass
        heapify(result)
        while len(result) > 1:
            try:
                while True:
                    key_value, order, value, _next = s = result[0]
                    yield value
                    value = _next()
                    # 替换 key_value、value
                    s[0] = key(value)
                    s[2] = value
                    # 替换堆顶元素
                    result[0] = s
                    sift_down_small(result, 0, len(result))
            except StopIteration:
                heappop(result)
        if result:
            _, value, _, _next = result[0]
            yield value
            yield from _next.__self__

以上我们就实现了整个 heapq 模块，如果把注释去掉，代码量还是很少的。那么接下来我们就来测试一下，看看实现的功能是否正确，以及两者的性能差异。

import random
import heapq
import my_heapq

data1 = [random.randint(1, 100000) for _ in range(100)]
data2 = data1.copy()
# 调整成相应的小根堆
heapq.heapify(data1)
my_heapq.heapify(data2)
# 再添加一些元素
for _ in range(100):
    value = random.randint(1, 100000)
    heapq.heappush(data1, value)
    my_heapq.heappush(data2, value)
# 将元素依次弹出，查看两个数组是否一样
# 如果一样，说明我们的实现是没有问题的
print(
    [heapq.heappop(data1) for _ in range(len(data1))]
    == [my_heapq.heappop(data2) for _ in range(len(data2))]
)  # True

# 验证 nlargest 和 nsmallest
data1 = [random.randint(1, 10000) for _ in range(100)]
data2 = data1.copy()
print(heapq.nlargest(5, data1) == my_heapq.nlargest(5, data2))  # True
print(heapq.nsmallest(5, data1) == my_heapq.nsmallest(5, data2))  # True

data1 = [{1: random.randint(1, 10000)} for _ in range(100)]
data2 = data1.copy()
print(
    heapq.nlargest(5, data1, key=lambda x: x[1])
    == my_heapq.nlargest(5, data2, key=lambda x: x[1])
)  # True
print(
    my_heapq.nsmallest(5, data2, key=lambda x: x[1])
    == heapq.nsmallest(5, data1, key=lambda x: x[1])
)  # True

# 验证 merge
print(
    list(heapq.merge([1,3,5,7], [0,2,4,8], [5,10,15,20], [], [25]))
    == list(my_heapq.merge([1,3,5,7], [0,2,4,8], [5,10,15,20], [], [25]))
)  # True

验证结果说明了我们自己实现的 heapq 是没有任何问题的，那么效率呢？效率如何呢？我们使用 jupyter notebook 比较一下：

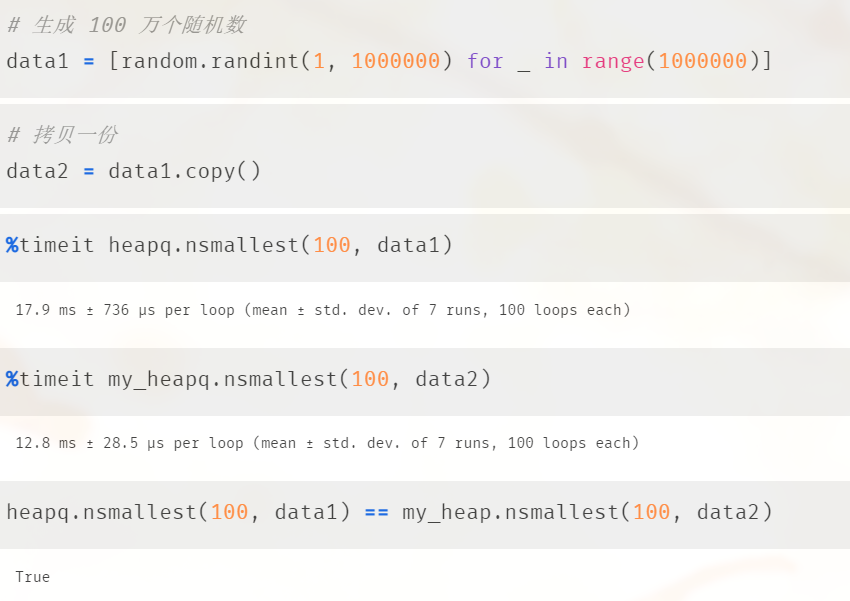
看样子是我们赢了，我们实现的要更快一些。

小结

以上就是堆相关的内容，我们说堆是一种非常高效的数据结构，它可以动态地添加、删除元素，并且时间复杂度均为 O(logN) 级别。这个特性就决定了它非常适合实现优先队列，只需要维护一个大根堆或者小根堆，在往堆中添加元素的时候，只需要加一个优先级即可，也就是将优先级和元素组合成一个元组添加到堆中。

当然了，如果你有一个一直在动态变化的数组，并且要随时获取里面的最小值或最大值，那么相比使用内置 min、max，更好的做法是将其维护成一个堆，然后通过 heappop 进行获取，因为这是一个 O(logN) 的操作，而是 min、max 是一个 O(N) 的操作。

最后我们还使用 Cython 手动实现了 heapq，当然这只是为了更好地理解堆这种数据结构，实际工作中没必要自己实现，直接使用现成的即可。