6.逻辑回归
1.什么是逻辑回归
在介绍逻辑回归之前,我们来看一张图
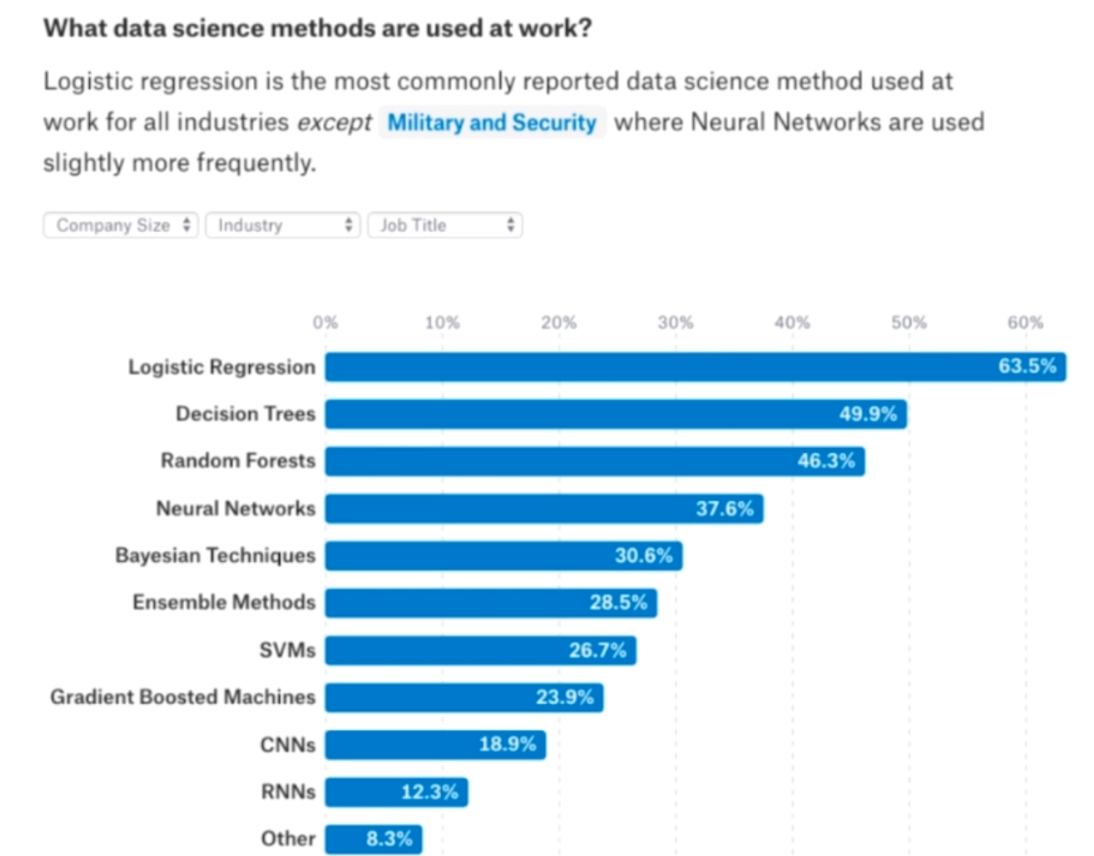
根据专业统计,逻辑回归是除了军事和安全领域之外,被使用频率最高的机器学习算法。所以逻辑回归的重要性不言而喻,尽管它很简单,但是很重要。所以没有最牛逼的算法,只是根据不同的场景,使用最合适的算法。
逻辑回归这个算法,听名字好像是一个回归算法,但它解决的是分类问题。可能这里有人就奇怪了,回归算法怎么解决分类问题,实际上逻辑回归的原理,是将样本的特征和样本发生的概率联系起来。换句话说我们计算样本发生的概率是多了,由于概率是一个数,所以我们把它叫做回归算法。
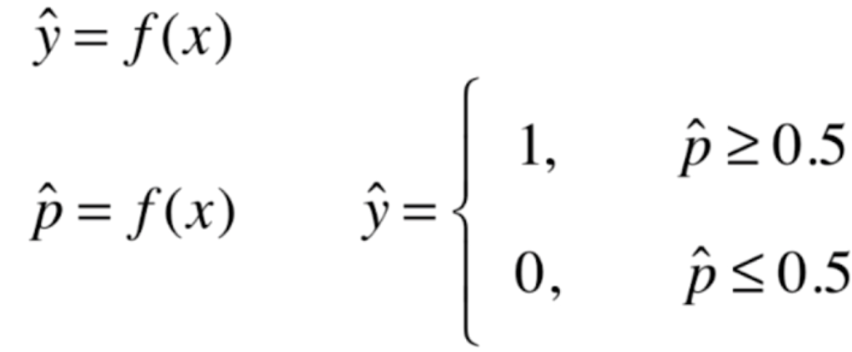
我们在线性回归当中,根据模型计算出一个具体的数值。比如房产预测计算的就是房产价格,成绩预测计算的就是分数。那么对于逻辑回归来说,我们计算的是一个概率p,如果p>=0.5,那么预测的结果就是1,p<=0.5,那么就是0。当然这个0和1代表的意义有实际情况决定,比如:1代表恶性肿瘤患者,0代表良性肿瘤患者。1代表银行给这个客户发放信用卡有风险,0代表没有风险等等等等。我们对得到的概率值多做一步操作,得到分类的结果
所以逻辑回归既可以看作是回归算法,也可以看做是分类算法。如果没有最后一步,那么得到结果就是一条概率曲线,是一个回归算法;但再根据概率是否大于0.5进行预测的话,那么就是一个分类算法。但通常作为分类算法用,只能用来解决二分类问题。
所以逻辑回归既可以看作是回归算法,也可以看做是分类算法。如果没有最后一步,那么得到结果就是一条概率曲线,是一个回归算法;但再根据概率是否大于0.5进行预测的话,那么就是一个分类算法。但通常作为分类算法用,只能用来解决二分类问题。
那么如何求出这个概率值呢?

首先我们可以看看线性回归,按照线性回归的思路,我们我们找到一组θ,让其与所有的样本Xb(当然里面包含X0恒等于1),进行点乘,得到一个值。但是呢?我们得到的这个值是任意的,是负无穷到正无穷之间,但是概率是在0到1之间。于是我们便想到,让得到的结果在作为一个参数,传到一个函数里面,然后将值映射到[0, 1]之间
那么这个σ是什么呢?
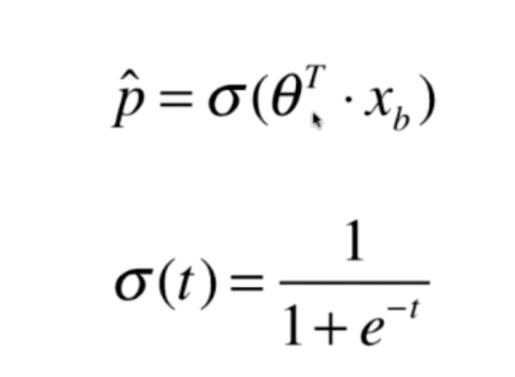
这个函数叫做sigmod函数,为什么是这个函数呢?我们编程实践一下
import numpy as np
import matplotlib.pyplot as plt
def sigmod(t):
return 1 / (1 + np.exp(-t))
x = np.linspace(-10, 10, 500)
y = sigmod(x)
plt.plot(x, y)
plt.show()

显然左端无限接近于零,右边无限接近于一,这正是我们想要的结果。

我们将之前函数带进去,就变成了如下结果
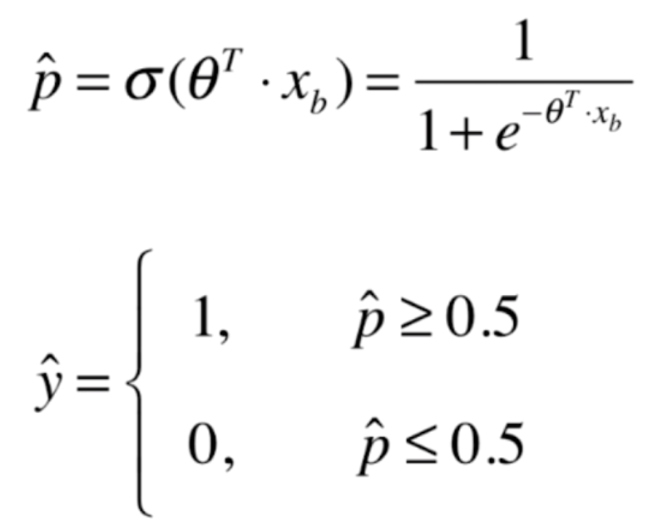
当p大于等于0.5,得到结果是1,p小于等于0.5,得到的结果是0
2.逻辑回归的损失函数
我们之前说了,让θ和Xb点乘,然后再传给σ函数,得到一个概率的估计值。如果值大于等于0.5,那么给样例分类为1,小于等于0.5,分类为0。但是现在的问题是我们怎么求出这个θ,我们可以想一下线性回归,在线性回归中,我们知道θ点乘Xb得到的就是估计值,我让估计值减去真实值,通过使得它们之间的误差最小,从而找到了最完美的θ。但是对于逻辑回归我们怎么做呢?可以像线性回归一样,但是又不等同于线性回归,它定义的方式比较复杂。我们可以想一下,当p大于等于0.5的话,我们分类为1,这说明0.51和0.99我们都分类为1。但是呢?在分类为1的前提下,显然p越大效果越好。同理在分类为0的前提下,p越小越好。如果p为0.51,那么尽管我们预测的结果是1,但是这个概率值正好处于边缘的情况,我们的模型是很有可能不小心就预测错了的。如果预测的p为0.8、0.85、0.9等等,那么我们可以很自信的说,这个样本的特征为1,但如果p为0.51或者0.49,那么我们说这个样本的特征为1或者0,是不是就显得很没有底气呢?因此,我们用这个来衡量模型的好坏或者损失

y=1:p越小,损失越大y=0:p越大,损失越大
那么我们只是单纯的比较p的大小吗?不是的,我们使用一个新的指标

我们将图像绘制出来,就显而易见了,注意:自变量的取值是0到1的
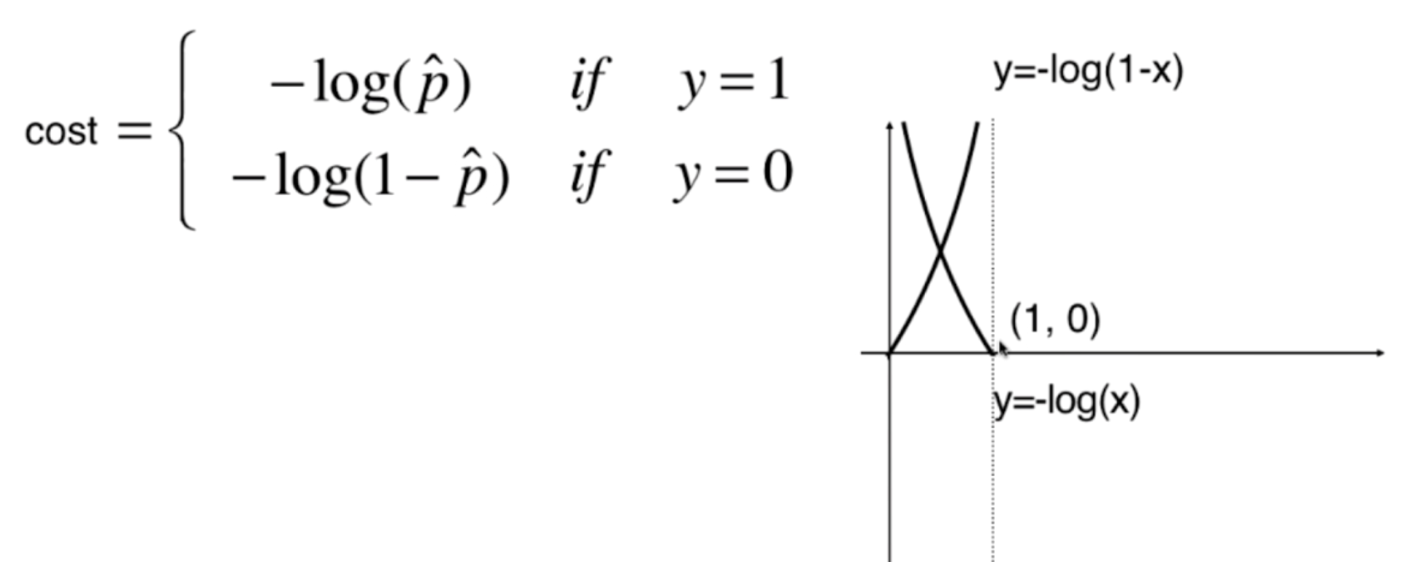
但是呢?这样还有一个问题,那就是损失函数变成了两个,于是我们可以将两者进行一下结合,就变成了这样
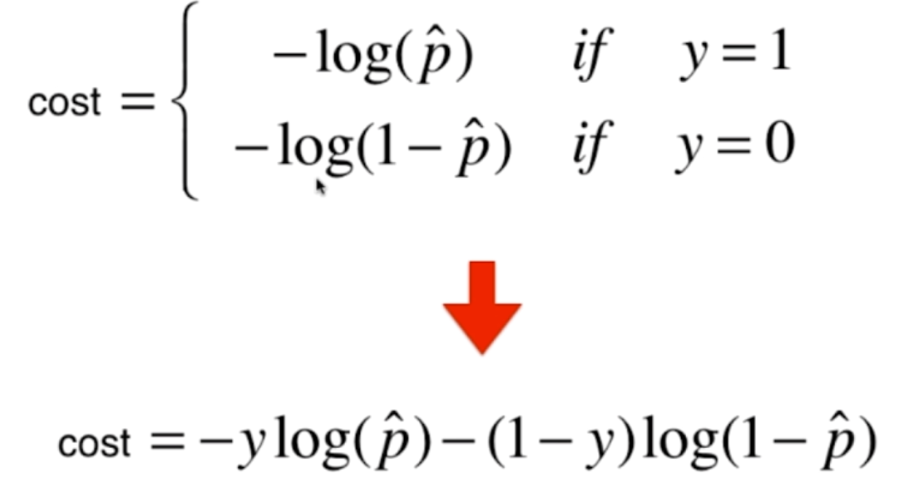
当y=1或者0的时候,其中1项就变成0了,得到结果和之前的是一样的,是不是很巧妙呢?那么对于m个样本,我们也是很容易求的
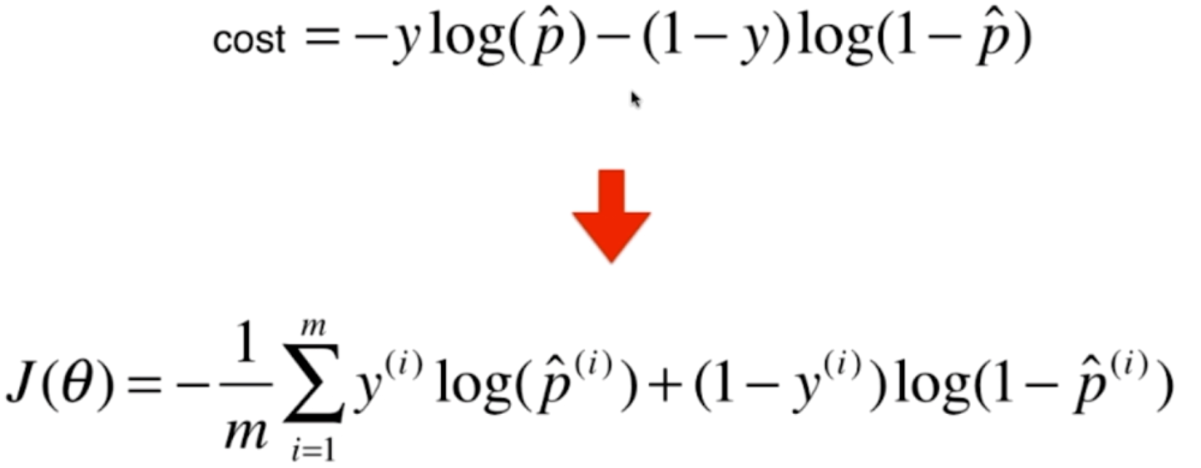
注意:此时的p_hat,是Xb·θ再传入sigmod函数的返回值
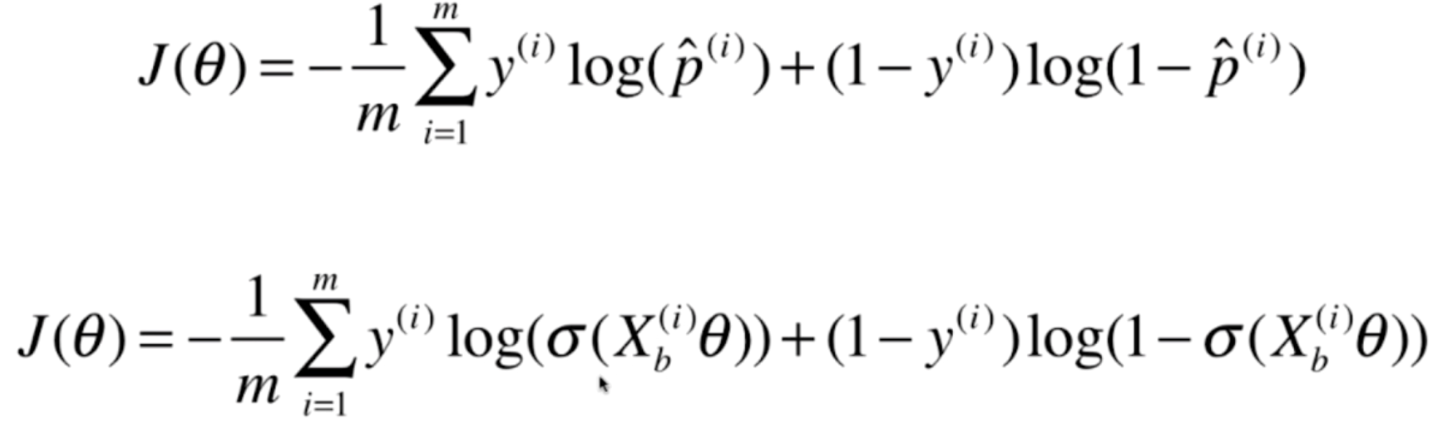
那么下面,我们的任务就是找到一组θ,使得这个函数达到最小值。但遗憾的是,这个函数不能像线性回归那样,求出一个公式解。因为这个函数是没有数学意义上的公式解的,但是我们可以使用梯度下降来求解,并且这个函数只有一个全局最优解。
3.逻辑回归损失函数的梯度
那么按照梯度下降的原理,我们要对损失函数梯度的每一个分量进行求导,我们可以先对梯度的一个分量进行求导,一个分量求出来了,剩余的分量是一样的。
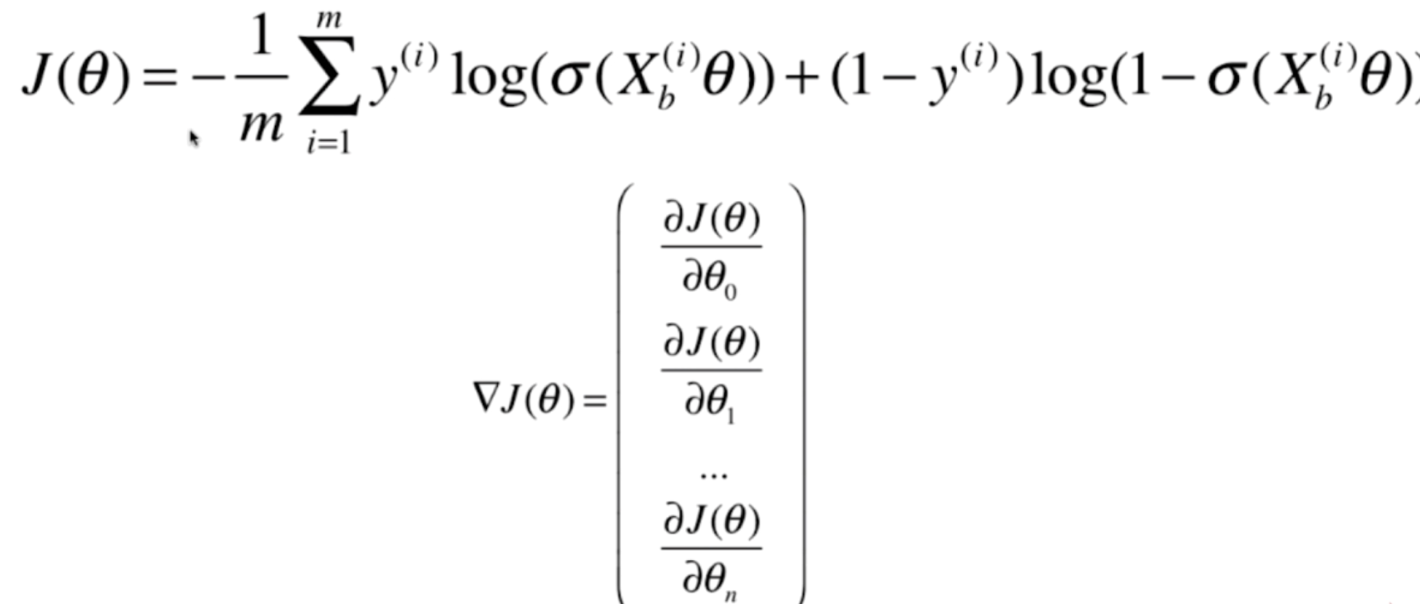
我们发现,这个式子求导虽然很麻烦,但是并不难。首先我们把Xbθ看成一个整体,先对σ求导,然后对log求导
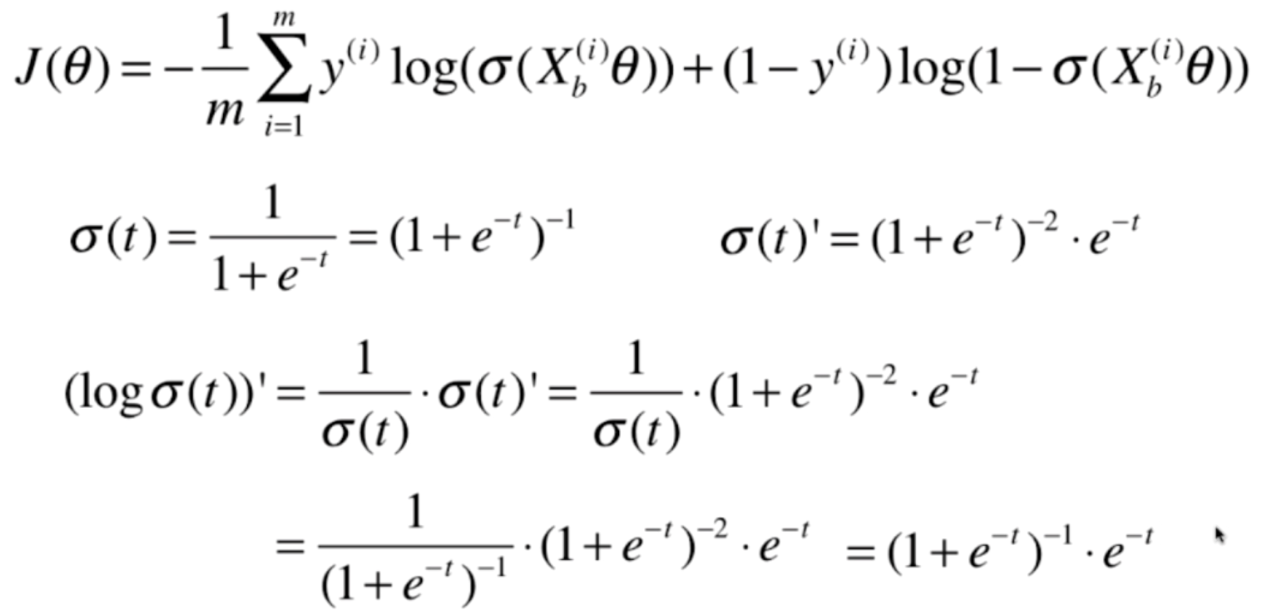
我们对log(σ(t))的导数继续做一下变换
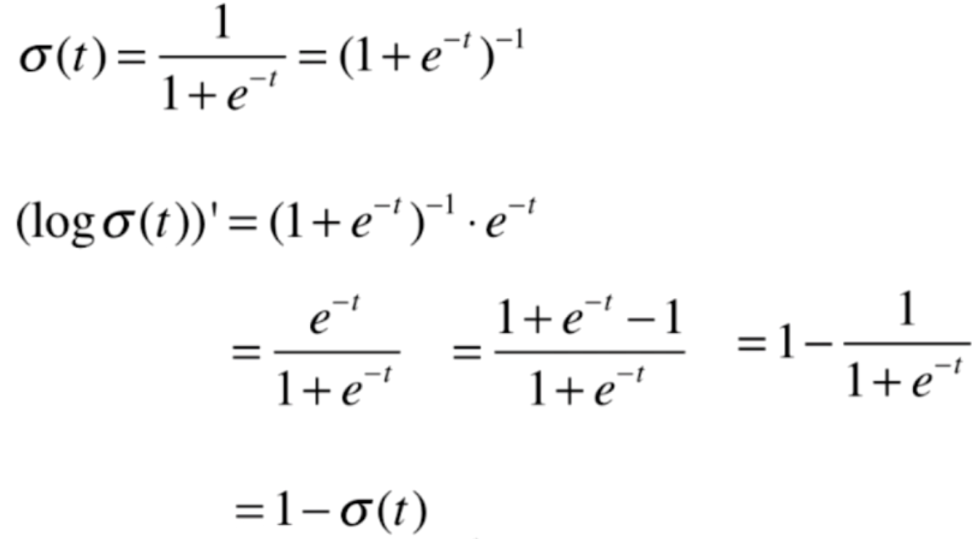
我们再来看一下原来的目标函数
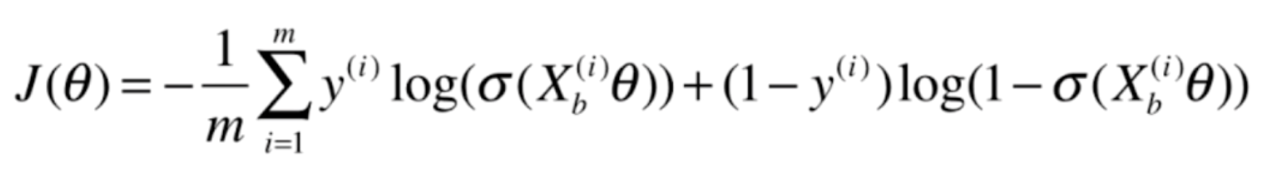
这个式子分成两部分,我们先对前半部分求导
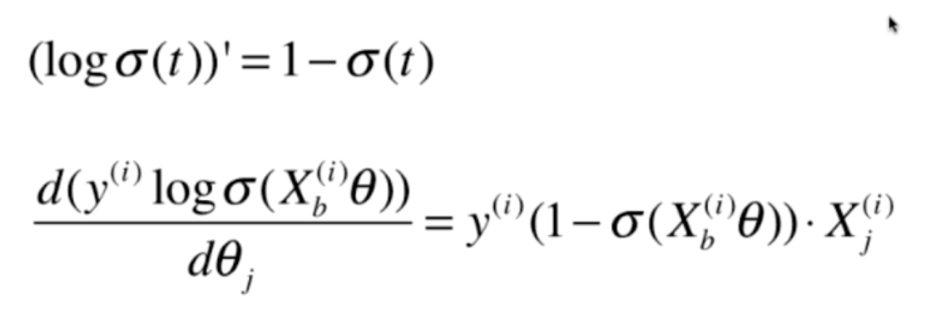
再对后半部分求导
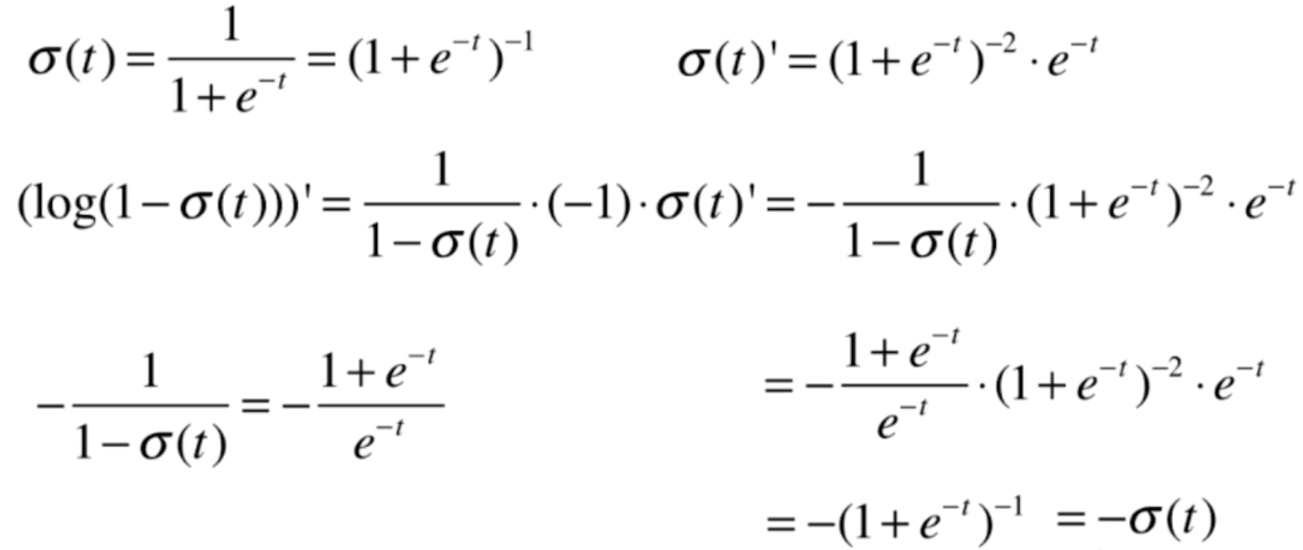
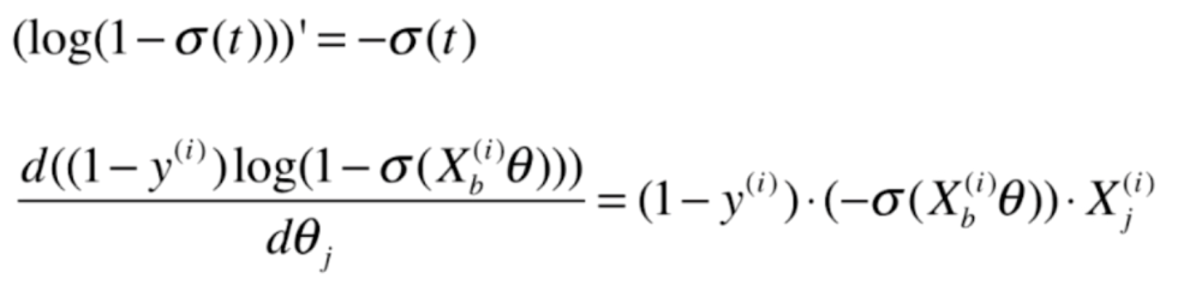
我们将式子整理一下,便求出了如下结果
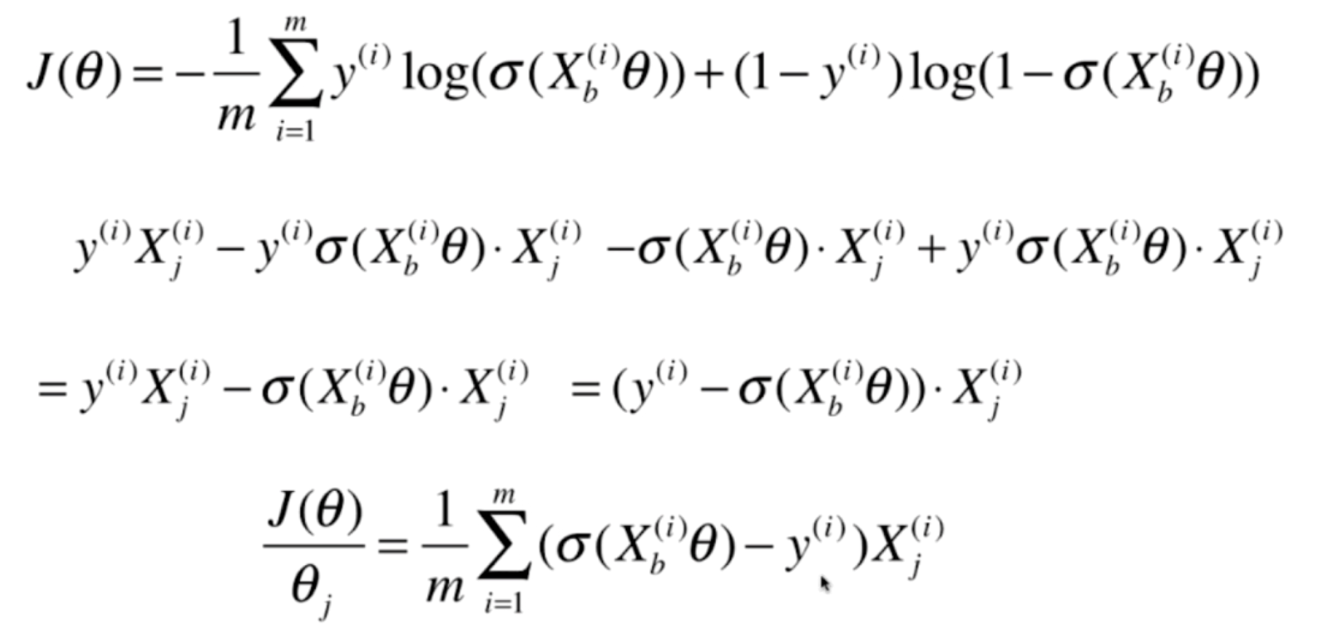
再进一步化简,就得到了J(θ)对θj的导数
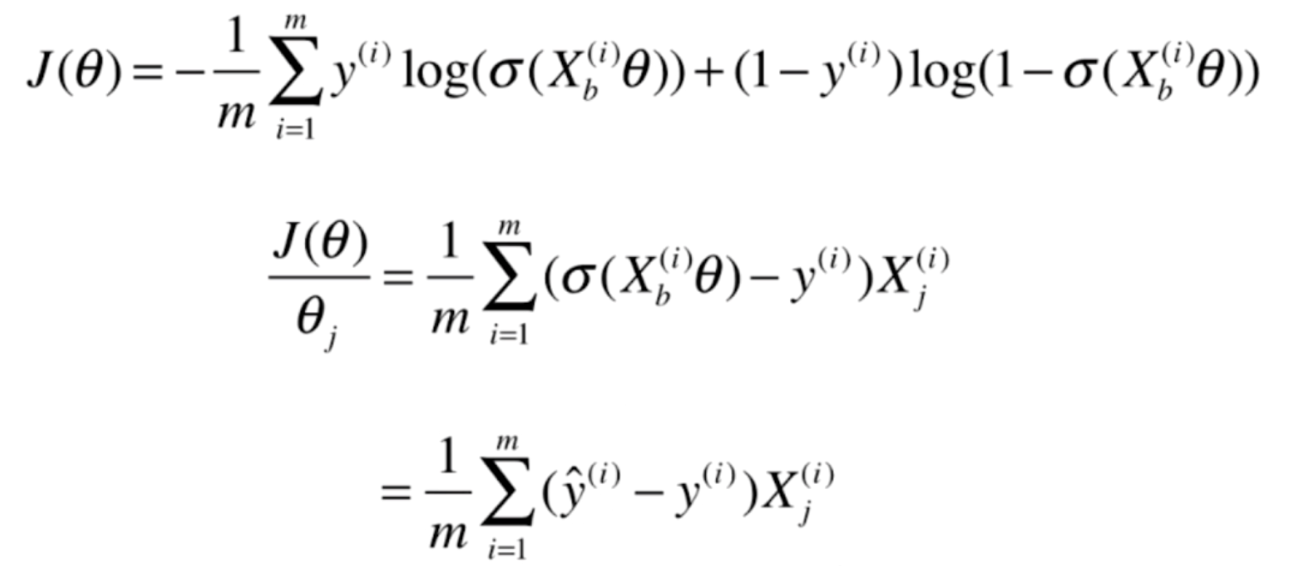
那么梯度就很好求了
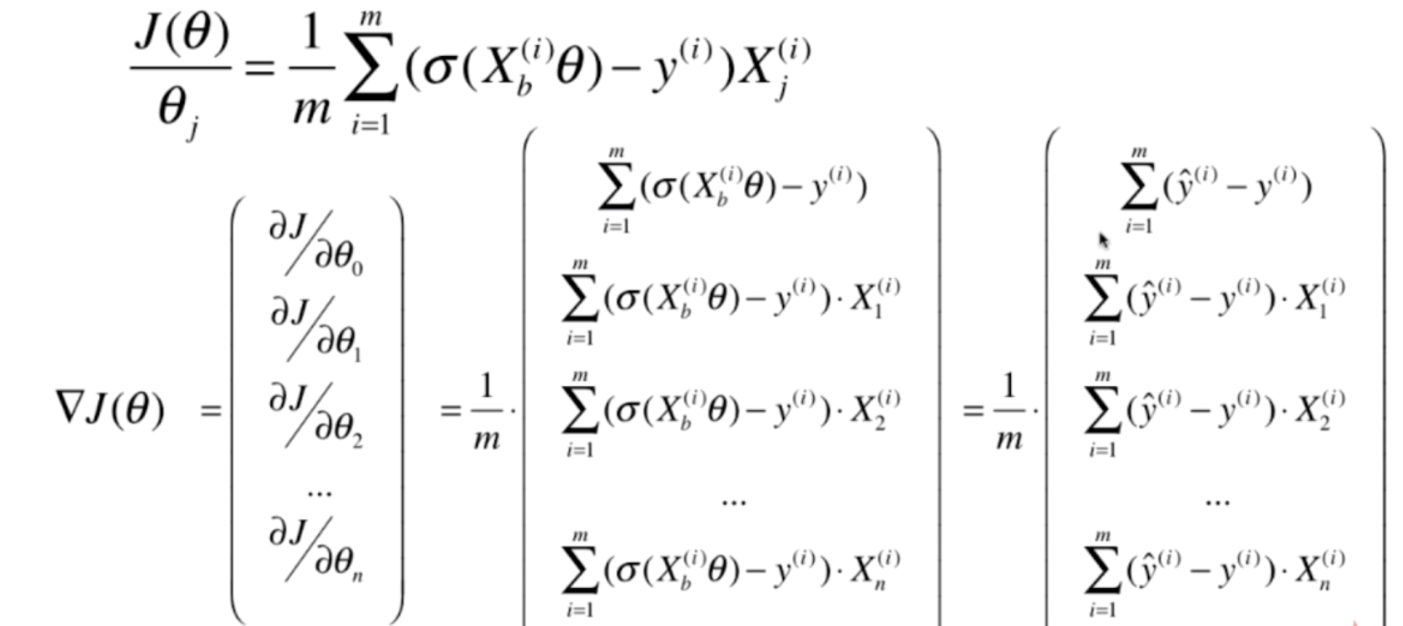
我们再来回忆一下线性回归,会发现两者有共同点

基本上是一样的,都是y的预测值减去y的真实值乘上X,只不过线性回归中的Xbθ在逻辑回归中,是σ(Xbθ),同时线性回归是矩阵外面的是2/m,逻辑回归是1/m
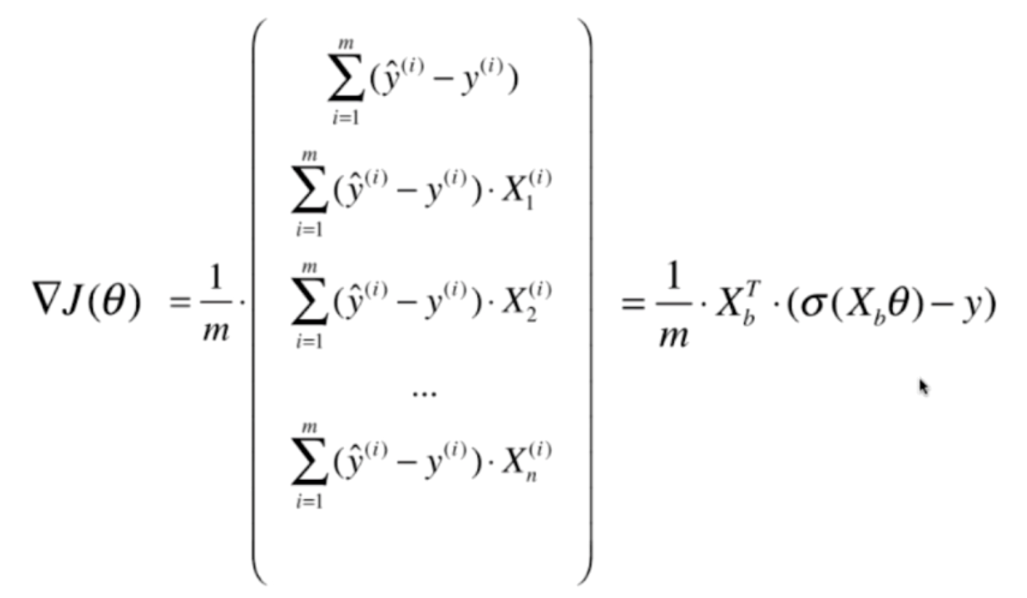
由线性回归对应的正规方程解,可以想象出逻辑回归的解。
4.实现逻辑回归算法
我们之前通过线性回归的正规方程解,得到逻辑回归的解,那么同样,我们来通过使用批量梯度下降法实现线性回归的方式,来实现逻辑回归。
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_iris
from sklearn.metrics import accuracy_score
class LogisticRegression:
def __init__(self):
self.coef_ = None
self.intercept_ = None
self._theta = None
def _sigmod(self, t):
return 1. / (1. + np.exp(-t))
def fit(self, X_train, y_train):
"""根据传入的X_train和y_train,使用批量梯度下降法来训练LogisticRegression的模型"""
assert X_train.shape[0] == y_train.shape[0], \
"the size of X_train must be equal to the size of y_train"
def J(theta, X_b, y):
y_hat = self._sigmod(X_b @ theta)
try:
return -np.sum(y * np.log(y_hat) + (1 - y) * np.log(1 - y_hat)) / len(y)
except Exception:
return float("inf")
def dJ(theta, X_b, y):
return X_b.T @ (self._sigmod(X_b @ theta) - y) / len(X_b)
def gradient_descent(X_b, y, initial_theta, eta=0.01, n_iters=1e4, epsilon=1e-8):
theta = initial_theta
cur_iter = 0
while cur_iter < n_iters:
gradient = dJ(theta, X_b, y)
last_theta = theta
theta = theta - eta * gradient
if abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon:
break
cur_iter += 1
return theta
X_b = np.c_[np.ones((len(X_train), 1)), X_train]
initial_theta = np.zeros(X_b.shape[1])
self._theta = gradient_descent(X_b, y_train, initial_theta)
self.intercept_ = self._theta[0]
self.coef_ = self._theta[1:]
return self
def predict_proba(self, X_predict):
"""给定X_predict,返回结果概率向量"""
assert self.intercept_ is not None, "must fit before predict"
assert len(self.coef_) == X_test.shape[1], \
"the feature number of X_predict must be equal to X_train"
X_b = np.c_[np.ones((len(X_predict), 1)), X_predict]
return self._sigmod(X_b @ self._theta)
def predict(self, X_predict):
assert self.intercept_ is not None, "must fit before predict"
assert len(self.coef_) == X_test.shape[1], \
"the feature number of X_predict must be equal to X_train"
proba = self.predict_proba(X_predict)
return np.where(proba >= 0.5, 1, 0)
def score(self, X_test, y_test):
y_predict = self.predict(X_test)
return accuracy_score(y_test,y_predict)
iris = load_iris()
X = iris.data
y = iris.target
# 为了可视化,我们只选取两个特征,并且结果我们只选两个
# 鸢尾花有4种,我们只选择两种,因为逻辑回归解决二分类任务
X = X[y < 2, :2]
y = y[y < 2]
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)
log_reg = LogisticRegression()
log_reg.fit(X_train, y_train)
# 由于样本简单,所以我们这里预测的准确度为1.0
print(log_reg.score(X_test, y_test)) # 1.0
查看属性
print(log_reg.intercept_) # -0.682738369899311
print(log_reg.coef_) # [ 3.01749692 -5.03046934]
print(np.round(log_reg.predict_proba(X_test), 5))
"""
[0.93293 0.98717 0.15541 0.01787 0.03909 0.01973 0.05215 0.99683 0.98092
0.7547 0.04738 0.00362 0.27123 0.03909 0.84902 0.80627 0.83574 0.33478
0.06922 0.21583 0.02401 0.18364 0.98092 0.98948 0.08342]
"""
5.决策边界
可以看到我们的逻辑回归是根据现行回归该的,线性回归所具有的参数和属性,逻辑回归也有。比截距和系数,这两者组合起来就是θ,那么这个θ有没有几何意义呢?我们应该如何看待呢?下面我们来介绍一下,其中包含一个对于分类问题来说,非常重要的一个概念,也就是决策边界。
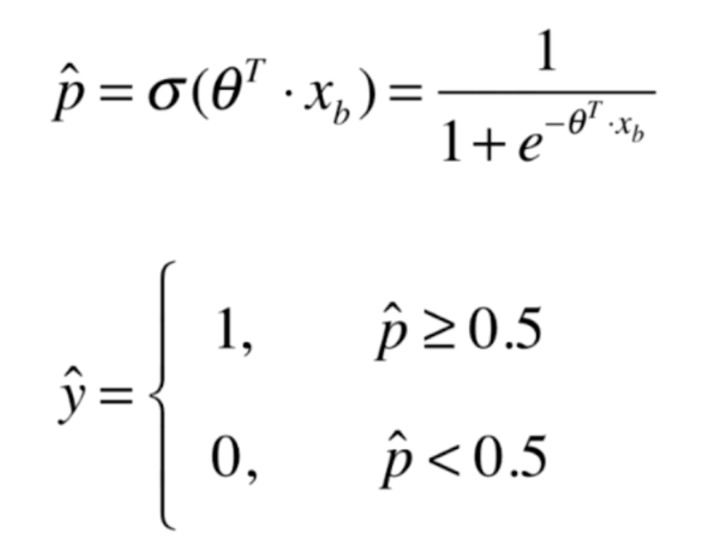
我们再来回顾一下逻辑回归的原理,我们找到了相应的参数θ,每当来一个样本,我们就会得到一个概率值,根据概率值是否大于0.5,我们来判断样本的特征是1还是0,那么当p等于0,也就是θ·Xb=0的时候,我们称之为决策边界
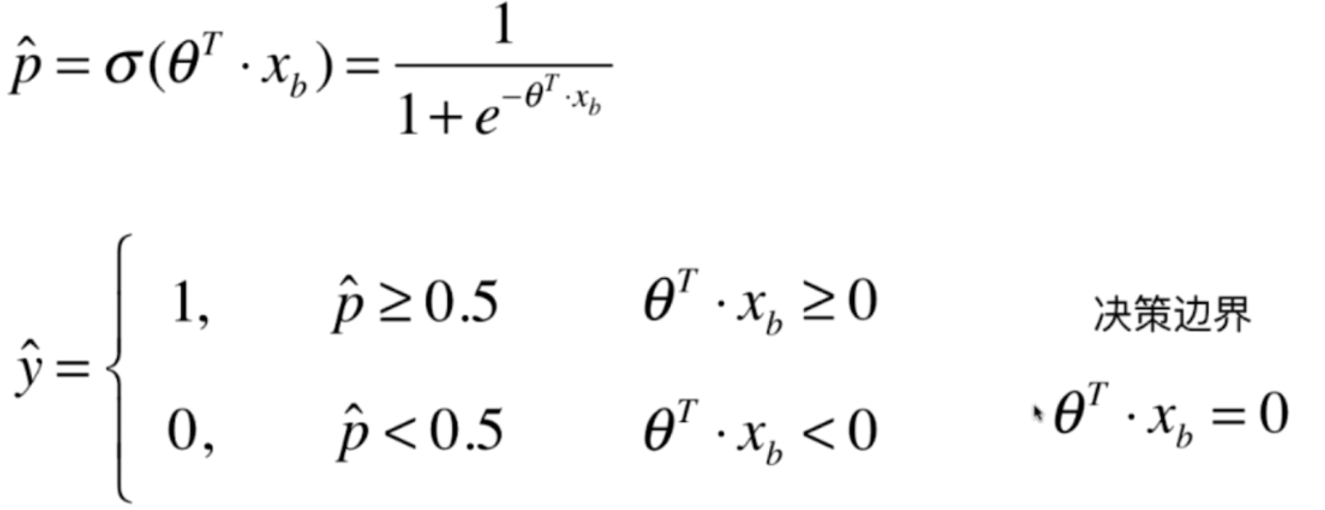
如果X有两个特征的话,那么θ·Xb=0就可以写成θ0 + θx1 + θx2=0,在二维坐标系中,我们把x2作为y轴,x1作为x轴,那么得到如下结果

我们具体实践来看一下
# 这里log_reg还是上节的代码
def x2(x1):
# x2 = (-θ0 - θ1x1) / θ2
return (-log_reg.intercept_ - log_reg.coef_[0] * x1) / log_reg.coef_[1]
# 如果把数据集绘制出来之后,横轴的范围大概在4到8左右,我们取1000个点
x1_plot = np.linspace(4, 8, 1000)
x2_plot = x2(x1_plot)
plt.scatter(X[y==0, 0], X[y==0, 1], color="red")
plt.scatter(X[y==1, 0], X[y==1, 1], color="green")
plt.plot(x1_plot, x2_plot)
plt.show()
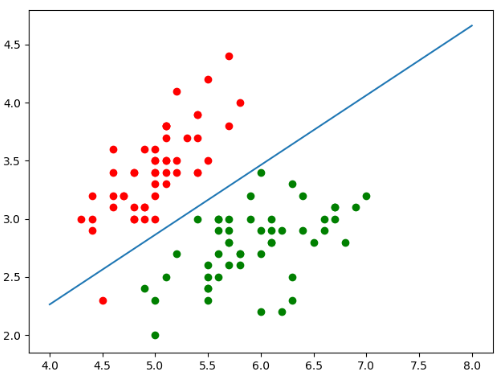
图中的蓝色直线就是我们的决策边界,如果点在蓝色的线上方,那么这个点就属于红色,在下方,就属于蓝色。如果在线上,那么我们就说这个点落在了决策边界上。如果落在了决策边界上,那么我们无论分类为1还是分类为0,都是正确的。但是正好落在决策边界上的情况比较少
但是我们发现,有一个红色的点落在了决策边界的下方,但是我们之前分类的准确度是又是1啊,这说明错误的点是在训练集上。
6.sklearn中的逻辑回归
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(666)
X = np.random.normal(0, 1, size=(200, 2))
y = np.array(X[:, 0] ** 2 + X[:, 1] < 1.5, dtype=np.int)
for _ in range(20):
y[np.random.randint(200)] = 1
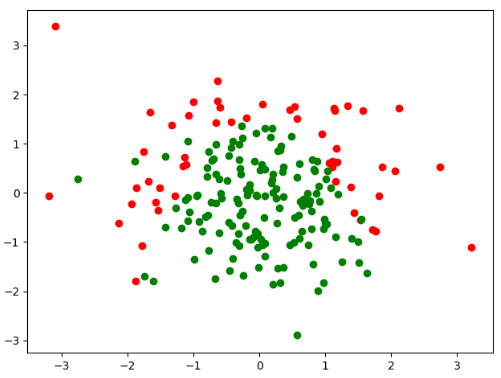
plt.scatter(X[y==0, 0], X[y==0, 1], color="red")
plt.scatter(X[y==1, 0], X[y==1, 1], color="green")
plt.show()
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
np.random.seed(666)
X = np.random.normal(0, 1, size=(200, 2))
y = np.array(X[:, 0] ** 2 + X[:, 1] < 1.5, dtype=np.int)
for _ in range(20):
y[np.random.randint(200)] = 1
X_train, X_test, y_train, y_test = train_test_split(X, y)
log_reg = LogisticRegression()
"""
def __init__(self, penalty='l2', dual=False, tol=1e-4, C=1.0,
fit_intercept=True, intercept_scaling=1, class_weight=None,
random_state=None, solver='warn', max_iter=100,
multi_class='warn', verbose=0, warm_start=False, n_jobs=None,
l1_ratio=None):
看一下sklearn的初始化构造函数,penalty项默认是l2,而C是1.0
"""
log_reg.fit(X_train, y_train)
print(log_reg.score(X_test, y_test)) # 0.8
7.OvR与OvO
我们之前说过逻辑回归只能用来解决二分类问题,但是我们稍加改造的话,也能让它支持多分类问题。改造的方式有两种,分别是OvR和OvO
OvR:One vs Rest,一对剩余的所有
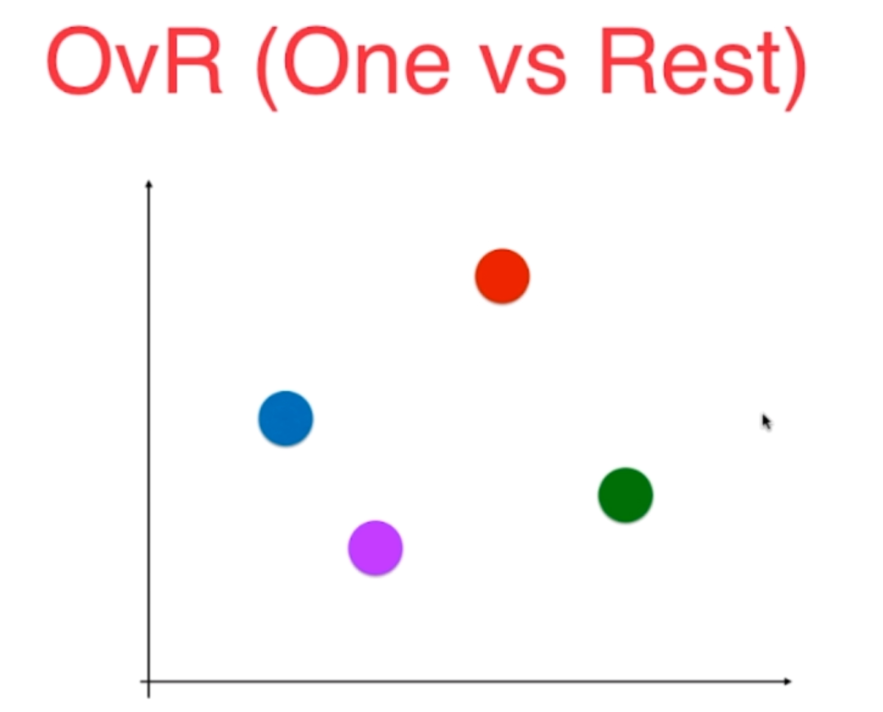
比如,我们选择红色的类别,那么我就将除了红色之外的都看成是一个类别,这就是Rest
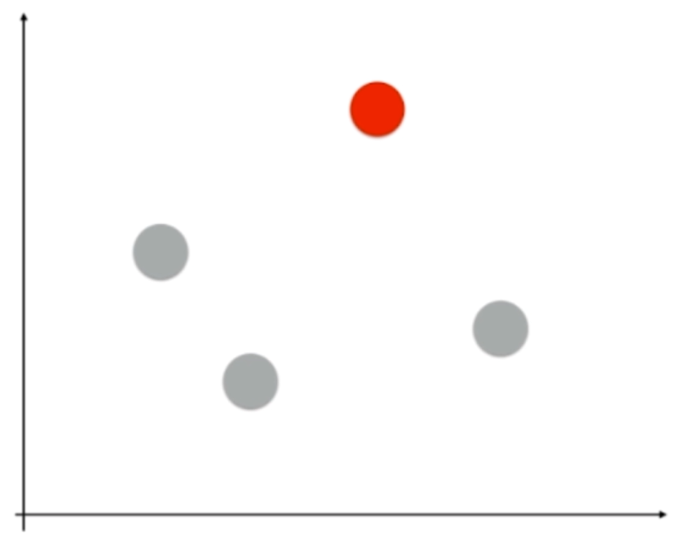
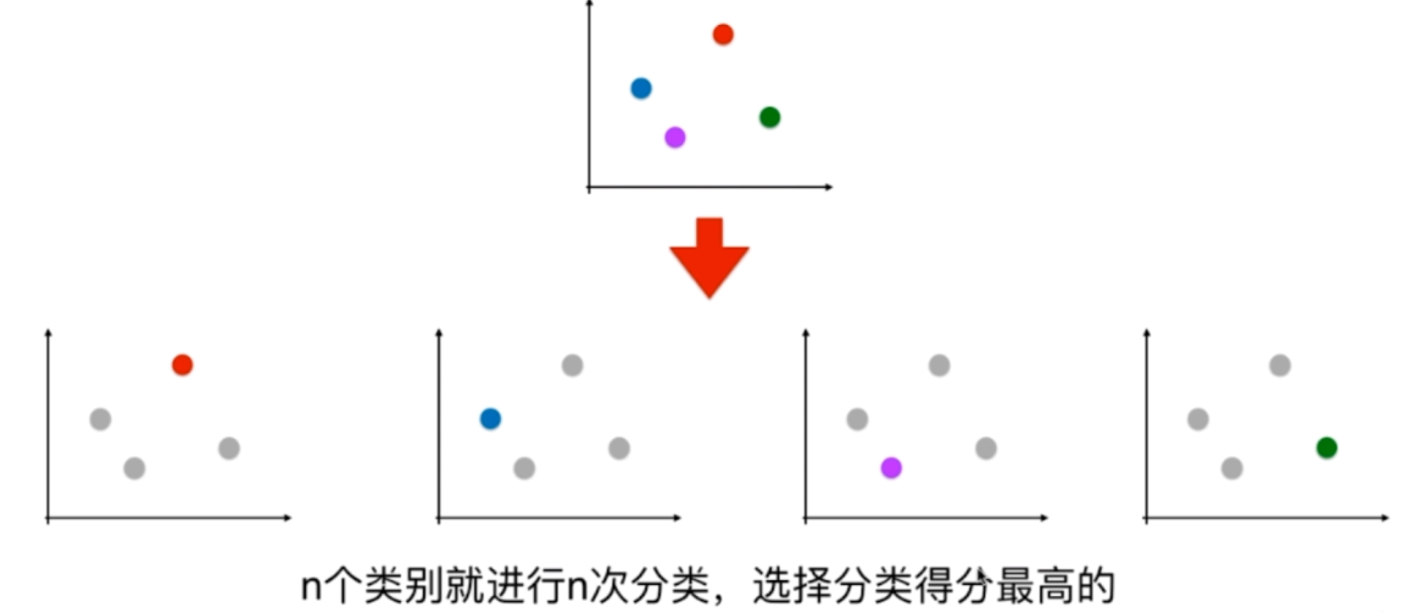
OvO:One vs One,一对一
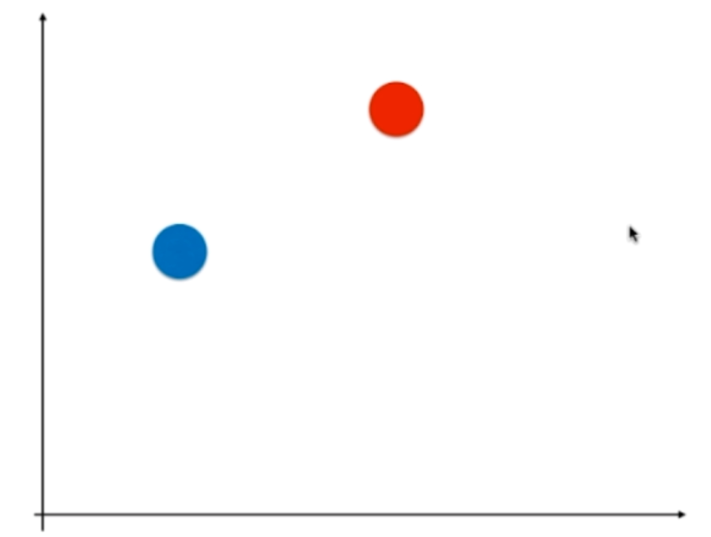
一对一,每次只选两个类别。如果有四个类别,那么总共有六个二分类问题。
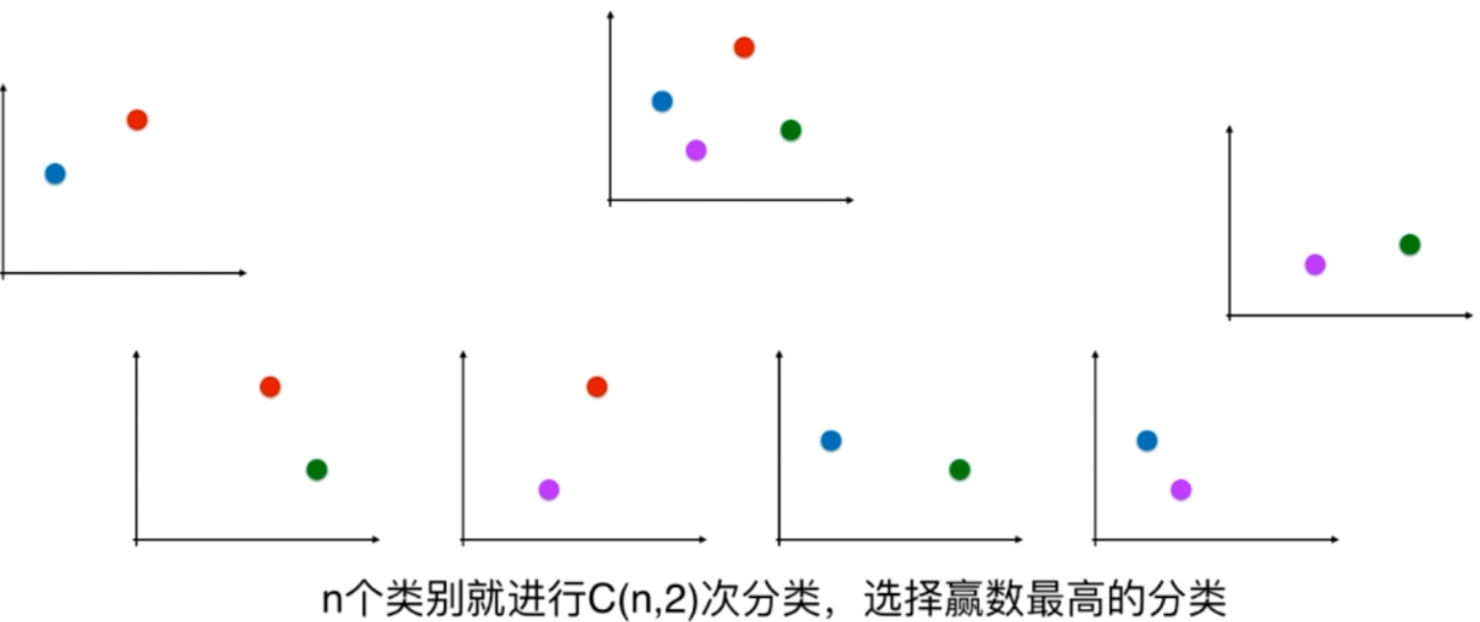
可以看到,OvO的时间复杂度是比OvR要高的,但是也越准确。
而sklearn中的逻辑回归是默认支持多分类的。
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import load_iris
# 注意到里面有一个参数叫做 multi_class,我们可以指定为OvR
log_reg = LogisticRegression(multi_class="ovr")
"""
def __init__(self, penalty='l2', dual=False, tol=1e-4, C=1.0,
fit_intercept=True, intercept_scaling=1, class_weight=None,
random_state=None, solver='warn', max_iter=100,
multi_class='warn', verbose=0, warm_start=False, n_jobs=None,
l1_ratio=None):
看一下sklearn的初始化构造函数,penalty项默认是l2,而C是1.0
"""
iris = load_iris()
X, y = iris.data, iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y)
log_reg.fit(X_train, y_train)
print(log_reg.score(X_test, y_test)) # 0.9473684210526315
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import load_iris
# 如果指定为OvO的话,那么指定为multinomial,但是要加上一个solver参数,这里指定为newton-cg
log_reg = LogisticRegression(multi_class="multinomial", solver="newton-cg")
"""
def __init__(self, penalty='l2', dual=False, tol=1e-4, C=1.0,
fit_intercept=True, intercept_scaling=1, class_weight=None,
random_state=None, solver='warn', max_iter=100,
multi_class='warn', verbose=0, warm_start=False, n_jobs=None,
l1_ratio=None):
看一下sklearn的初始化构造函数,penalty项默认是l2,而C是1.0
"""
iris = load_iris()
X, y = iris.data, iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y)
log_reg.fit(X_train, y_train)
print(log_reg.score(X_test, y_test)) # 1.0
使用OvO的准确率达到了1.0,之前也说过,OvO的准确率是要高一些的。
此外,sklearn还直接为我们提供了两个ovr和ovo的类,我们只需要传入一个基本的逻辑回归实例即可
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import load_iris
from sklearn.multiclass import OneVsOneClassifier, OneVsRestClassifier
log_reg = LogisticRegression()
iris = load_iris()
X, y = iris.data, iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y)
ovr = OneVsRestClassifier(log_reg)
ovr.fit(X_train, y_train)
print(ovr.score(X_test, y_test))
ovo = OneVsOneClassifier(log_reg)
ovo.fit(X_train, y_train)
print(ovo.score(X_test, y_test))
如果觉得文章对您有所帮助,可以请囊中羞涩的作者喝杯柠檬水,万分感谢,愿每一个来到这里的人都生活愉快,幸福美满。
微信赞赏

支付宝赞赏



 浙公网安备 33010602011771号
浙公网安备 33010602011771号